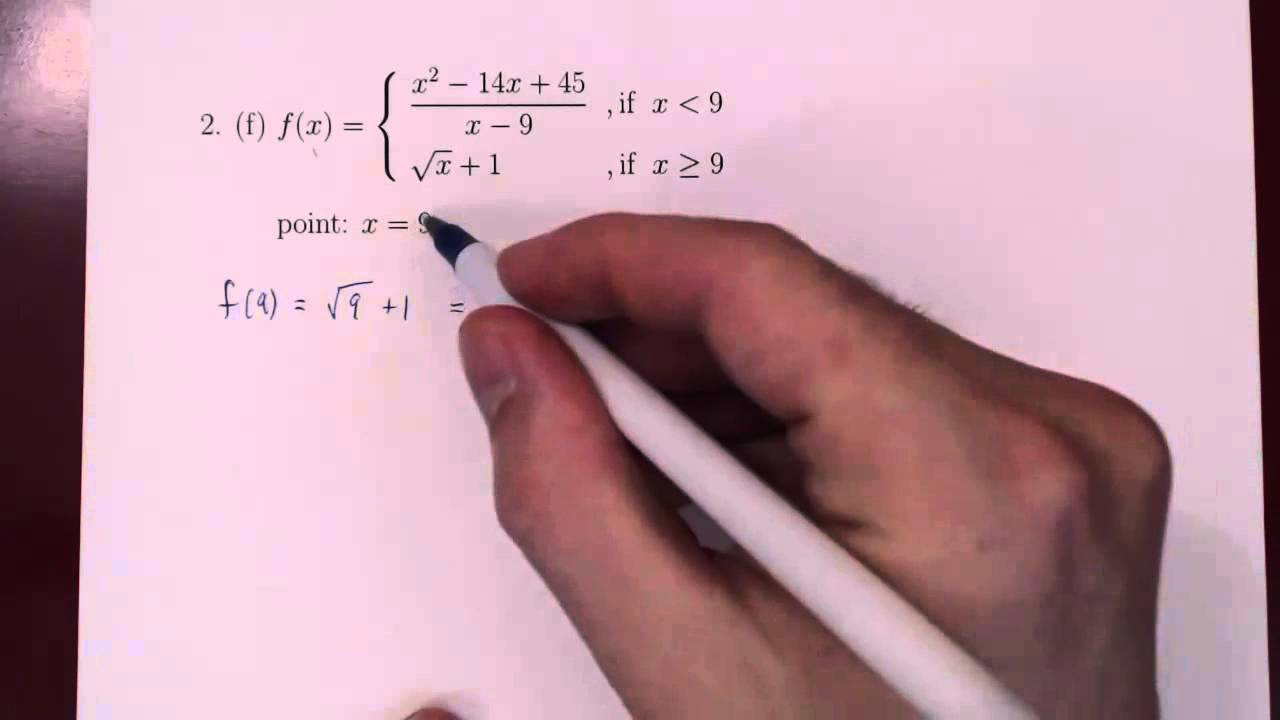Using the Definition of Continuity in Calculus
TLDRThe video script discusses the concept of continuity in mathematics, focusing on piecewise functions. It explores the conditions for a function to be continuous at a specific point, which involves checking if the limit as x approaches that point equals the function's value at that point. The script presents several problems sourced from a college board document, guiding viewers through the process of determining continuity for different piecewise functions. It covers straightforward cases where the function is continuous and more complex scenarios requiring the use of L'Hôpital's rule to find the limit. The detailed explanation helps viewers understand how to approach and solve problems related to function continuity, emphasizing the importance of limits and their role in defining continuous functions.
Takeaways
- 📘 The definition of continuity for a function at a point is that the limit as x approaches that point of the function equals the function's value at that point.
- 📌 To determine if a piecewise function is continuous at a certain point, calculate the limit from the left and right and check if they are equal and also equal to the function's value at that point.
- 🔍 For the function j(x), it is continuous at x=1 because the left and right limits as x approaches 1 are equal and match the function's value at x=1, which is 2.
- 🚫 The function k(x) is not continuous at x=2 because the left and right limits as x approaches 2 are not equal; the left limit is 2, and the right limit is 1.
- 🔁 Flipping the piecewise function's order for l(x) results in a continuous function at x=2, as both the left and right limits are 1, which matches l(2).
- 🤔 The function r(x) is a piecewise function involving a ratio of two functions and an additional constant c when x=0. It requires finding the correct value of c for continuity at x=0.
- 📉 To find the limit as x approaches 0 for r(x), consider the behavior of the numerator m(x) and the denominator p(1-x) separately, using limits and potentially L'Hôpital's rule.
- 📚 L'Hôpital's rule is applied when dealing with the indeterminate form 0/0, by taking the derivative of the numerator and denominator and re-evaluating the limit.
- 🔢 The limit of r(x) as x approaches 0 is found to be -2 by applying L'Hôpital's rule, which requires calculating the derivatives of the numerator and denominator.
- 🎯 To ensure continuity of r(x) at x=0, the value of c must be set such that the limit as x approaches 0 of r(x) equals r(0), which leads to c being determined as -2.
- 🧮 The process involves understanding the concept of limits, applying them to piecewise functions, and using L'Hôpital's rule for indeterminate forms, showcasing a deeper level of calculus.
Q & A
What is the definition of continuity for a function at a point?
-A function is continuous at x equals c if the limit as x approaches c of f of x is equal to f of c.
What is the piecewise function j(x) defined as in the transcript?
-The function j(x) is defined as m(x) when x is less than or equal to 1, and as 2e^(x^2 - 1) when x is greater than 1.
How is the continuity of j(x) at x=1 determined?
-The continuity of j(x) at x=1 is determined by checking if the limit as x approaches 1 of j(x) exists, j(1) exists, and they are equal.
What is the value of the limit as x approaches 1 from the left for j(x)?
-The value of the limit as x approaches 1 from the left for j(x) is 2.
What is the value of j(1) in the given piecewise function?
-The value of j(1) is m(1), which is 2 based on the graph provided in the transcript.
Why is the function k(x) not continuous at x=2 according to the transcript?
-The function k(x) is not continuous at x=2 because the limit from the left (which is 2) does not equal the limit from the right (which is 1).
What is the piecewise function l(x) defined as in the transcript?
-The function l(x) is defined as p(x) when x is less than or equal to 2, and as m(x) when x is greater than 2.
How is the continuity of l(x) at x=2 determined?
-The continuity of l(x) at x=2 is determined by checking if the limit as x approaches 2 of l(x) is equal to l(2), which are both found to be 1.
What is the piecewise function r(x) defined as in the transcript?
-The function r(x) is defined as m(x)/p(1 - x) when x is not zero, and r(x) is defined as c when x is 0.
What value of c makes r(x) continuous at x=0?
-The value of c that makes r(x) continuous at x=0 is -2, as determined by setting the limit as x approaches 0 of r(x) equal to r(0).
What mathematical rule was used to find the limit as x approaches 0 of r(x)?
-L'Hôpital's rule was used to find the limit as x approaches 0 of r(x), which resulted in a simplified form of 0/0.
What is the final step to ensure r(x) is continuous at x=0?
-The final step is to set the limit as x approaches 0 of r(x) equal to r(0), which is c, and solve for c to ensure continuity at x=0.
Outlines
📚 Understanding Continuity Through Piecewise Functions
The video begins by introducing the concept of continuity in functions, specifically focusing on a piecewise function j(x). The presenter discusses how to determine if j(x) is continuous at x=1 by checking if the limit as x approaches 1 of j(x) equals j(1). The function j(x) is defined differently for x less than or equal to 1 and for x greater than 1. The presenter calculates the limit from both the left and the right, finding them to be equal to 2, and then confirms that j(1) also equals 2, thus concluding that j(x) is continuous at x=1.
🔍 Analyzing Discontinuity in Piecewise Functions
The second paragraph delves into another piecewise function, k(x), to determine its continuity at x=2. The function k(x) is defined as m(x) for x less than 2 and p(x) for x greater than or equal to 2. The presenter evaluates the limit from the left and the right as x approaches 2 and finds that they are not equal (2 from the left and 1 from the right). This discrepancy indicates that k(x) is not continuous at x=2, as the limits from both sides do not match.
🎯 Continuity Assessment with Flipped Piecewise Conditions
In the third paragraph, the roles of m(x) and p(x) are reversed in the piecewise function l(x), defined as p(x) for x less than or equal to 2 and m(x) for x greater than 2. The presenter again examines the limit from the left and right as x approaches 2, finding that both are equal to 1. Additionally, l(2) is identified as p(2), which also equals 1. Since all these values align, the presenter concludes that l(x) is continuous at x=2.
🧮 Applying L'Hôpital's Rule for Continuity with Composition Functions
The final paragraph presents a more complex piecewise function, r(x), which is defined as the ratio of two functions m(x) and p(x) for x not equal to zero, with an additional condition that r(x) equals a constant c when x is 0. The goal is to find the value of c that ensures the continuity of r(x) at x=0. The presenter uses L'Hôpital's rule to handle the indeterminate form 0/0 that arises when finding the limit as x approaches 0. After applying the rule and calculating the derivatives, the presenter finds that the limit as x approaches 0 of r(x) is -2. By setting this equal to r(0), which is defined as c, the presenter determines that c must be -2 for r(x) to be continuous at x=0.
Mindmap
Keywords
💡Continuity
💡Limit
💡Piecewise Function
💡L'Hôpital's Rule
💡Derivative
💡Chain Rule
💡Indeterminate Form
💡Function Value
💡Substitution
💡Graph
💡Slope
Highlights
The video discusses the definition of continuity for functions, emphasizing the importance of the limit as x approaches a certain value being equal to the function's value at that point.
The presenter uses problems from a college board document released during COVID to illustrate the concept of continuity.
A piecewise function j(x) is analyzed for continuity at x equals 1, involving evaluating limits from the left and right.
The function j(x) is found to be continuous at x=1 as the left and right limits are equal and match the function's value at that point.
For the function k(x), the limits from the left and right as x approaches 2 are not equal, indicating discontinuity at x=2.
The video demonstrates how to handle piecewise functions and their continuity by evaluating the function's behavior at the 'break points'.
The function l(x) is shown to be continuous at x=2 after evaluating the left and right limits and finding them to be equal to the function's value.
A more complex piecewise function r(x) is introduced, which includes a ratio of two functions and a constant c.
To ensure continuity of r(x) at x=0, the limit as x approaches zero is evaluated, resulting in an indeterminate form of 0/0.
L'Hôpital's rule is applied to find the limit of r(x) as x approaches zero, which involves taking the derivative of the numerator and the denominator separately.
The derivative of the numerator m'(x) at x=0 is found to be 2, and the derivative of the denominator p'(1-x) at x=0 is found to be -1.
Applying L'Hôpital's rule yields a limit of -2 for r(x) as x approaches zero.
To maintain continuity at x=0, the constant c in the function r(x) is determined to be equal to the limit, which is -2.
The video provides a comprehensive approach to understanding and solving problems related to the continuity of piecewise functions.
The use of L'Hôpital's rule in the context of continuity is highlighted as a key technique for handling indeterminate forms.
The presenter emphasizes the importance of evaluating the function's value at the point in question, in addition to the limits, to determine continuity.
The video concludes with a reminder of the steps to determine continuity, including evaluating limits from both directions and comparing them to the function's value.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: