CALCULUS SPEEDRUN || Limits || Episode 1

Dr. Trefor Bazett

9 Dec 202112:42

EducationalLearning

32 Likes 10 Comments

TLDRIn this engaging first episode of the calculus speed run series, the host dives into solving actual test problems on limits with the aim of completing calculus in record time. The episode begins with a piecewise function challenge to find the value of 'c' that ensures continuity. Using a graphical approach and mathematical computations, the host determines 'c' to be 10. The second problem tackles a peculiar limit involving sine and cotangent functions, cleverly leveraging a fundamental limit to simplify the expression and arrive at the answer, three-quarters. The third problem involves a square root and requires algebraic manipulation to avoid an indeterminate form, leading to a solution of one-half. The fourth problem, a limit as x approaches infinity, is approached by focusing on the highest power of x, resulting in an answer of the square root of 3 divided by 2. The final problem explores the limit of an exponential function as x approaches 1 from the right, using the continuity of the exponential function to find the answer, which is zero. Throughout the episode, the host emphasizes the importance of understanding and applying fundamental limits, showcasing the power of Maple Learn for verifying solutions. This episode is a must-watch for those studying for calculus exams or seeking a comprehensive review of limits.

Takeaways

📚 The series aims to tackle calculus test problems, starting with limits, which is beneficial for both test preparation and review.
🔗 For a comprehensive understanding of limits, the presenter recommends checking out the full calculus playlist provided in the description.
📋 The first problem involves a piecewise function with an unknown constant 'c', and the goal is to find the value of 'c' that makes the function continuous.
📈 The presenter uses a graphical approach and a slider to visually understand the function's continuity before computing the exact value of 'c'.
✅ By setting the left and right limits equal to each other and to the function value at x=2, the presenter finds that 'c' equals 10, which aligns with the graphical intuition.
🤔 The second problem deals with a seemingly complex limit involving sine and cotangent functions, which is solved by leveraging a fundamental limit property.
🧮 In the third problem, the presenter uses the radical conjugate method to simplify the expression and find the limit as x approaches 1.
🚀 For the fourth problem, the presenter approaches a limit involving square roots and infinity by focusing on the highest power of 'x' in the expression.
📉 The fifth problem involves the limit of an exponential function as x approaches 1 from the right, which is solved by considering the behavior of the function graphically.
🌐 The presenter emphasizes the usefulness of Maple Learn for verifying answers and understanding the process of solving calculus problems.
🎓 The video concludes with an encouragement to like the video for the YouTube algorithm and to check out Maple Learn for further mathematical insights.

Q & A

What is the main topic of the first episode of the calculus speed run series?
-The main topic of the first episode is limits, focusing on understanding and solving problems related to this concept in calculus.
What is the purpose of the slider for the parameter 'c' in the first problem?
-The slider for the parameter 'c' is used to visually understand how changes in 'c' affect the continuity of the piecewise function and to find the value of 'c' that makes the function continuous.
What is the key limit formula used in the second problem to solve for the limit as x approaches 0 of sine(3x) times cotangent(4x)?
-The key limit formula used is the limit as x approaches 0 of sine(x)/x, which is equal to 1. This formula is applied after expressing cotangent in terms of sine and cosine.
How does the process of taking the limit as x approaches 1 from the right in the third problem help in finding the value of the function at x=1?
-The process ensures that the limit from the right and the limit from the left are equal, which must also equal the function value at x=1 for the function to be continuous at that point.
What algebraic trick is used in the third problem to deal with the square root and the indeterminate form 0/0?
-The algebraic trick used is the radical conjugate method, which involves multiplying the numerator and denominator by the conjugate of the expression within the square root.
What is the approach taken to solve the fourth problem, which involves a limit as x goes to infinity?
-The approach involves analyzing the highest power of x in the numerator and denominator and considering the behavior of the function as x becomes very large, effectively ignoring lower order terms.
How does the use of Maple Learn in the video help verify the solutions to the calculus problems?
-Maple Learn is used to evaluate the limits and provide immediate feedback, helping to verify the correctness of the solutions as they are being worked out.
What is the final answer to the second problem involving the limit of sine(3x) times cotangent(4x) as x approaches 0?
-The final answer to the second problem is three quarters, or 3/4.
In the fourth problem, what is the quick guess for the limit without doing a rigorous calculation?
-The quick guess for the limit as x goes to infinity is the square root of 3 divided by 2.
What property of the exponential function is used in the fifth problem to find the limit as x approaches 1 from the right?
-The property that e is a continuous function is used, allowing the problem to be transformed into finding the limit of e to the power of (1/(1-x)) as x approaches 1 from the right.
What is the final answer to the fifth problem involving the limit of e to the power of (1-x) as x approaches 1 from the right?
-The final answer to the fifth problem is 0, as e to the power of minus infinity is 0.

Outlines

00:00

📚 Introduction to Calculus Speed Run Series

This paragraph introduces the first episode of a calculus series focused on solving test problems. The series aims to cover all of calculus, starting with limits. It is intended for students preparing for tests or those who want a calculus review. The speaker encourages viewers to check out a full calculus playlist for foundational concepts and to try the problems themselves using a provided Maple Learn document. The video is sponsored by Maple Learn, and the first problem involves finding the value of 'c' for a piecewise function to be continuous.

05:00

🔍 Analyzing Continuity and Limits

The speaker discusses the process of determining the value of 'c' for the piecewise function to be continuous. They use a graphical approach with a slider for 'c' to visually assess the function's continuity. The focus is on the limit as 'x' approaches 2 from both the right and left sides, aiming for the function value at 'x=2' to match the limits. The speaker then performs the actual computation, using the left-hand limit and right-hand limit to solve for 'c', which they find to be 10, aligning with their initial graphical intuition.

10:01

🧮 Solving Limits with Trigonometric Functions

The second problem involves finding the limit as 'x' approaches 0 of the product of sine(3x) and cotangent(4x). The speaker categorizes this as a 'weird' problem but one that fits a standard category involving a well-known limit. They use the limit of sine(x)/x as x approaches 0, equal to 1, to simplify the expression. By manipulating the terms and applying the limit, they find the answer to be three quarters, verified using Maple Learn.

🔢 Dealing with Indeterminate Forms

The third problem involves finding the limit as 'x' approaches 1 of a square root expression. The speaker notes that directly plugging in 'x=1' leads to an indeterminate form and instead opts to use the radical conjugate method. They simplify the expression by canceling out terms and applying the limit, resulting in a final answer of one half, confirmed by Maple Learn.

🚀 Limits at Infinity

The fourth problem deals with a limit as 'x' approaches infinity. The speaker quickly identifies that the highest power of 'x' in the expression will dominate and simplifies the problem by focusing on these terms. They then rigorously justify their initial guess by multiplying the numerator and denominator by a suitable term to facilitate the limit calculation, which results in the answer being the square root of 3 divided by 2.

📉 Limits of Exponential Functions

The fifth problem involves finding the limit as 'x' approaches 1 from the right of e to the power of (1 - x). The speaker uses the property of continuity of the exponential function and manipulates the expression to find the limit. They graph the function and its components to understand the behavior as 'x' approaches 1. The speaker concludes that the limit is 0, as e to the power of negative infinity equals 0, a result confirmed by Maple Learn.

Mindmap

Keywords

💡Limits

Limits are a fundamental concept in calculus that describe the behavior of a function as its input approaches a particular value. In the video, limits are the primary topic, with various examples and problems demonstrating how to calculate them. They are essential for understanding continuity and differentiability in calculus.

💡Piecewise function

A piecewise function is a function that is defined by multiple sub-functions, each applicable to a different interval of the function's domain. In the video, the first problem involves a piecewise function with an unknown constant 'c', and the goal is to find the value of 'c' that makes the function continuous.

💡Continuity

Continuity in calculus refers to a function being unbroken and smooth without any gaps or jumps in its graph. The video discusses the concept of continuity in the context of a piecewise function, aiming to find a value that ensures there are no jumps at the point where the function definition changes.

💡Indeterminate form

An indeterminate form occurs when an expression's limit is not immediately clear, often because it simplifies to a form like 0/0 or ∞/∞. In the video, the third problem involves an indeterminate form, which is resolved using algebraic manipulation, specifically the method of rationalizing the denominator.

💡Rational functions

Rational functions are mathematical expressions that can be represented as the quotient of two polynomials. They are mentioned in the video in the context of discussing the continuity of functions, noting that rational functions are continuous wherever the denominator is not zero.

💡Conjugate

In the context of the video, the conjugate refers to the algebraic technique used to simplify expressions involving square roots, particularly when dealing with differences of squares. The method of taking the conjugate is used in problem three to resolve an indeterminate form and find the limit.

💡Exponential function

An exponential function is a function of the form e^x, where e is the base of the natural logarithm, approximately equal to 2.71828. The video touches on exponential functions when discussing the limit as x approaches 1 from the right of e to the power of (1 - x), highlighting the continuity and properties of exponential functions.

💡Cotangent

Cotangent is a trigonometric function that is the reciprocal of the tangent function, defined as cot(x) = 1/tan(x). In the second problem of the video, the cotangent of 4x is expressed in terms of sines and cosines to leverage a standard limit involving sine and x as x approaches zero.

💡Standard limit

A standard limit refers to a limit with a well-known result that is frequently used in calculus. The video emphasizes a particular standard limit: lim (x->0) [sin(x)/x] = 1, which is used to solve the second problem involving the product of sine and cotangent functions.

💡Maple Learn

Maple Learn is an online platform for mathematics education, mentioned in the video as a sponsor and a tool for verifying the solutions to calculus problems. The video demonstrates how Maple Learn can be used to check the answers to the various limit problems discussed.

💡Graphs

Graphs are visual representations of functions, showing the relationship between the input and output variables. The video uses graphs to illustrate the behavior of functions, particularly when discussing limits and the continuity of piecewise functions.

Highlights

The series aims to solve actual calculus test problems, starting with limits.

A full calculus playlist is available for those new to the subject.

Maple Learn document lists all problems for viewers to try themselves.

Sponsor Maple Learn is featured, providing tools for problem-solving.

A piecewise function's continuity is explored, with an unknown value of c.

Graphical intuition is used to estimate the value of c for continuity.

The limit as x approaches 2 from both sides is calculated for the piecewise function.

The value of c is determined to be 10, ensuring the function's continuity.

A limit involving sine and cotangent of x is solved using standard limits.

The limit is simplified by recognizing and applying the limit of sine(x)/x as x approaches 0.

The final answer for the sine and cotangent limit is three quarters.

Maple Learn is used to verify the correctness of the calculated limit.

A limit involving a square root is tackled by using the radical conjugate method.

The radical conjugate simplifies the expression, making the limit easier to evaluate.

The limit as x approaches 1 of the square root expression is found to be one half.

A limit as x approaches infinity is addressed by focusing on the highest power of x.

The limit is simplified by factoring out 1/x, leading to the answer of √3/2.

The limit as x approaches 1 from the right of e^(1-x) is evaluated using continuity properties of e^x.

The final answer for the e^(1-x) limit is 0, as the function approaches negative infinity.

The video concludes with an encouragement to like and subscribe for more calculus content.

Transcripts

Browse More Related Video

BusCalc 05 Limits Examples Pt 1

Limit examples w/ brain malfunction on first prob (part 4) | Differential Calculus | Khan Academy

my all-in-one calculus question

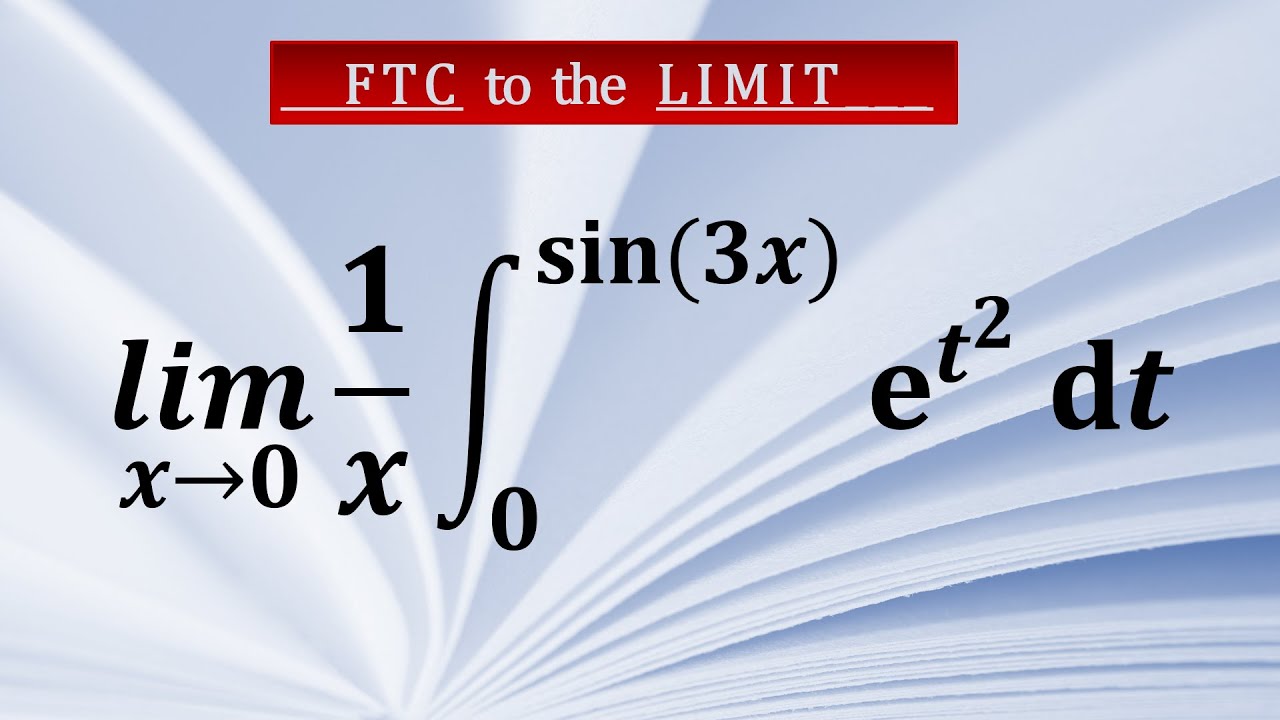
Limit problem with Fundamental Theorem of Calculus

One Sided Limits of Piecewise Functions - Calculus

Limits at infinity of quotients with square roots (even power) | AP Calculus AB | Khan Academy