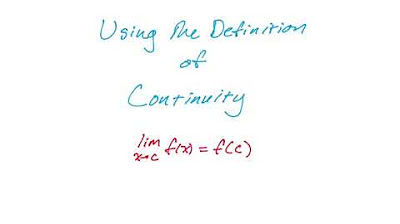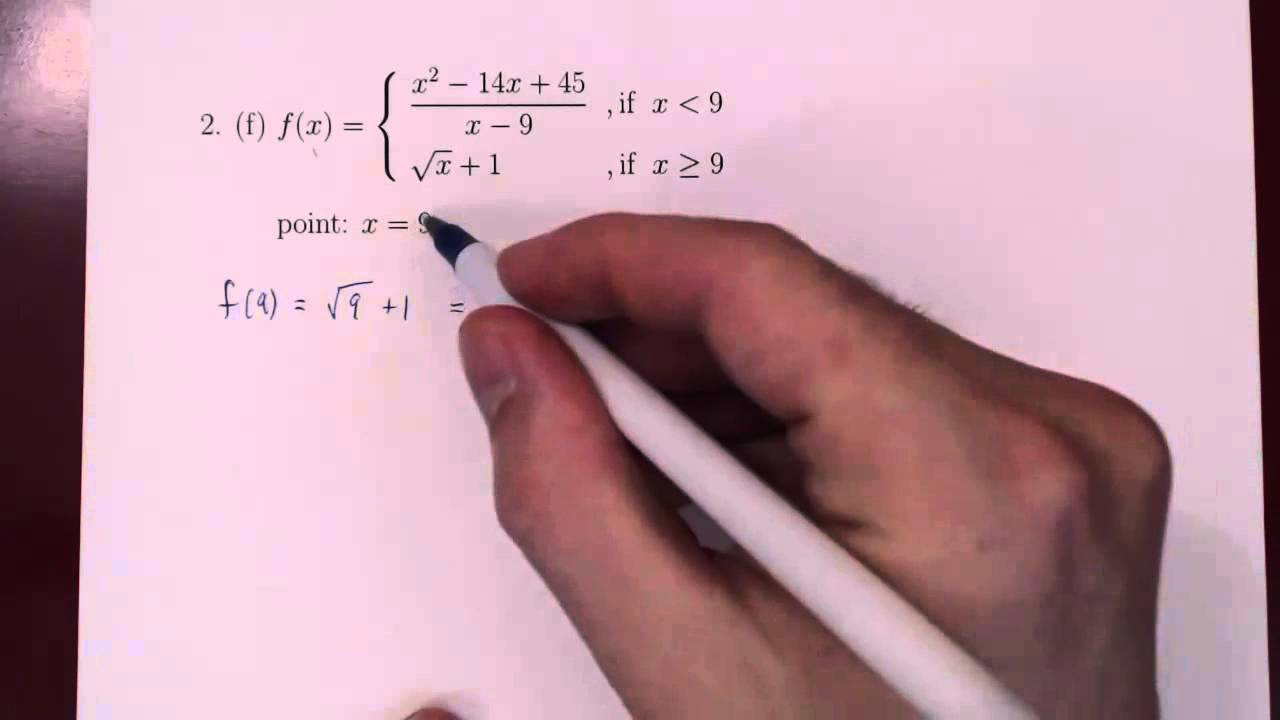AP Calculus AB Crash Course Day 3 - Limits, Continuity, and Differentiation
TLDRThe video script is an in-depth exploration of various calculus problems, focusing on continuity, limits, and derivatives. It begins with a function g(x) and demonstrates how to find its value at a specific point by factoring and using limits. The script then tackles two different methods for finding the limit of a trigonometric function as h approaches zero, using both the definition of the derivative and L'Hôpital's rule. It continues with a discussion on limits at infinity and how to handle piecewise functions, showing that a function f is continuous at a certain point by comparing the left and right limits with the function's value at that point. The script also examines the continuity of another piecewise function g at a specific point. It concludes with an analysis of a differential equation, sketching a slope field, a solution curve, and describing the points where the derivative equals negative one. This comprehensive script serves as an educational resource for understanding calculus concepts.
Takeaways
- 📐 The function g is continuous for all real numbers and is defined as g(x) = (x^2 - x - 6) / (x - 3) for x ≠ 3. The value of g(3) is found by factoring the numerator and using the limit concept, resulting in g(3) = 5.
- 🧮 To find the limit of a function as it approaches a certain value, factorization can be used to simplify expressions and cancel out terms, as demonstrated with the function g(x).
- 🔢 The limit of (tan(π/4 + h) - tan(π/4)) / h as h approaches zero can be found using the definition of the derivative, which in this case leads to the derivative of tan(x) at x = π/4, resulting in a value of 2.
- 📚 L'Hôpital's rule can be applied to the indeterminate form 0/0 to find the limit by taking the derivative of the numerator and denominator and then evaluating the limit as before, which also results in 2 for the given example.
- 🚀 When finding the limit of a rational function as x approaches infinity, the highest power of x in the numerator and denominator determines the limit, which in the provided example is 3.
- 🧵 To show that a piecewise function is continuous at a certain point, one must check the limit from both the left and the right and ensure it equals the function's value at that point, as demonstrated with the function f(x) at x = 7.
- 🔍 For a piecewise function to be continuous at a point, the limits from the left and right must exist and be equal to the function's value at that point, as shown with the function g(x) at x = 4.
- 📈 To find relative maxima of a function, one must identify critical points where the derivative is zero and then analyze the sign of the derivative around these points to determine the function's behavior, as illustrated with the function f(x) on the interval [0, 3].
- 🤔 The points where the derivative of a function equals zero are potential candidates for relative maxima or minima, but the function's behavior around these points must be considered to confirm.
- 📉 The slope field of a differential equation can be sketched by evaluating the derivative at specific points, which gives the slope of the solution curve at those points.
- 📍 For a given differential equation, the solution curve passing through a specific point can be sketched by following the slope field and considering the domain of the function.
- 🔑 To find points where the derivative of a function equals a specific value, such as -1, one can set the derivative equal to that value and solve for y in terms of x, resulting in the equation of a line.
Q & A
How can the function g(x) = (x^2 - x - 6) / (x - 3) be simplified and why is this important for finding g(3)?
-The function g(x) = (x^2 - x - 6) / (x - 3) can be simplified by factoring the numerator as (x - 3)(x + 2). This simplification is important because it allows the (x - 3) terms to cancel out, eliminating the discontinuity at x = 3 and enabling the computation of g(3) as the limit of g(x) as x approaches 3, which results in g(3) = 5.
What is the derivative of tan(x) and how is it used to find the limit of the function as h approaches zero?
-The derivative of tan(x) is sec^2(x). This derivative is used to solve the limit as h approaches zero of the expression [tan(π/4 + h) - tan(π/4)] / h, by recognizing it as a derivative at π/4. This leads to the limit being sec^2(π/4), which calculates to 2.
What is L'Hopital's Rule and how is it applied in the context of finding the limit of tan(π/4 + h) - tan(π/4) all over h?
-L'Hopital's Rule is a method used to solve limits of indeterminate forms like 0/0 by taking the derivative of the numerator and the denominator. In the case of [tan(π/4 + h) - tan(π/4)] / h, applying L'Hopital's Rule involves differentiating tan(π/4 + h) to get sec^2(π/4 + h), which simplifies the limit to sec^2(π/4) = 2 when h = 0.
How do you find the limit as x approaches infinity for the function (5 - x^2 + 3x^3) / (x^3 - 2x + 3)?
-To find the limit as x approaches infinity for the function (5 - x^2 + 3x^3) / (x^3 - 2x + 3), you should focus on the highest power of x in both the numerator and the denominator. As x approaches infinity, the terms with lower powers of x become negligible, so the limit simplifies to the ratio of the coefficients of the highest power terms, which is 3/1 = 3.
What steps are necessary to prove that a function is continuous at a certain point?
-To prove that a function is continuous at a point, you need to show that: 1) the function is defined at that point, 2) the limit of the function as it approaches that point exists, and 3) the limit equals the function's value at that point. Each of these conditions must be verified from both the left and the right sides of the point if applicable.
How can you determine if a piecewise function is continuous at a point where the formula changes?
-To determine if a piecewise function is continuous at a point where the formula changes, calculate the limit from the left and the limit from the right of that point using the respective formulas for each side. If both limits exist and equal each other, and also match the function's value at that point, the function is continuous there.
What does it mean if the derivative of a function is zero at a point?
-If the derivative of a function is zero at a point, it indicates that there is a critical point, which could be a local maximum, local minimum, or a point of inflection. The behavior of the function around this point needs to be analyzed further to determine the exact nature of the critical point.
In the context of differential equations, what is a slope field and how is it useful?
-A slope field is a graphical representation showing the slopes of tangent lines to solutions of a differential equation at a variety of points in the coordinate plane. It helps visualize the behavior of solutions and can aid in sketching approximate solution curves that pass through given points.
What is the purpose of computing the limit from both the left and the right for a function at a specific point?
-Computing the limit from both the left and the right for a function at a specific point helps determine if the function is continuous at that point.
Outlines
📚 Calculus Continuity and Limits
The first paragraph discusses the continuity of a function g and how to find its value at a specific point (x=3). The function g(x) is defined as x^2 - x - 6 / (x - 3) for all x not equal to 3. To find g(3), the script factors x^2 - x - 6 into (x - 3)(x + 2) and then uses the limit concept to simplify the expression as x approaches 3, resulting in g(3) = 5. The paragraph also covers two methods for finding the limit as h approaches zero of (tan(pi/4 + h) - tan(pi/4)) / h: using the definition of the derivative and L'Hôpital's rule, both yielding the same result of 2.
🔍 Limits at Infinity and Continuity
The second paragraph deals with limits at infinity and the continuity of piecewise functions. It begins by explaining how to find the limit as x approaches infinity of a rational function by disregarding lower order terms. The limit of five minus x squared plus three x cubed over x cubed minus two x plus three simplifies to three, as the highest power of x cancels out. The paragraph then demonstrates how to prove the continuity of a piecewise function f at x equals seven by comparing the left and right limits and ensuring they match the function's value at that point. Lastly, it discusses another piecewise function g and uses the definition of continuity to show that g is continuous at x equals four.
📈 Critical Points and Differential Equations
The third paragraph focuses on identifying relative maxima of a differentiable function f on a closed interval [0, 3] using a provided table of function values and derivatives. It explains that relative maxima occur at critical points where the derivative is zero. By analyzing the sign of the derivative, the paragraph determines that there is only one relative maximum at x equals two. The paragraph also addresses a differential equation dy/dx = y + 1/x and sketches a slope field for twelve specified points. It then sketches the solution curve passing through the point (-1, 0) for y greater than negative one and describes all points in the x-y plane where dy/dx equals negative one, which corresponds to the line y = -x - 1.
Mindmap
Keywords
💡Continuity
💡Limit
💡Factoring
💡Derivative
💡L'Hôpital's Rule
💡Piecewise Function
💡Critical Numbers
💡Differential Equation
💡Slope Field
💡Relative Maximum
💡Indeterminate Form
Highlights
The function g is continuous for all real numbers and is defined as g(x) = x^2 - x - 6 / (x - 3) for all x not equal to 3.
The function g(x) can be factored into (x - 3)(x + 2) to simplify the expression.
The value of g(3) is computed using the limit as x approaches 3, which results in g(3) = 5.
Two methods are presented to find the limit as h approaches zero of (tan(π/4 + h) - tan(π/4)) / h: using the definition of the derivative and L'Hôpital's rule.
The derivative of tan(x) is sec^2(x), and sec^2(π/4) is found to be 2.
L'Hôpital's rule is applied to the limit, resulting in the derivative of the numerator, sec^2(π/4 + h), over the derivative of the denominator, which is 1.
The limit as x approaches infinity of (5 - x^2 + 3x^3) / (x^3 - 2x + 3) is found by canceling out the highest power of x, resulting in 3.
The function f is piecewise defined and shown to be continuous at x = 7 by evaluating the limit from the left and right and comparing it to f(7).
The function g is also piecewise defined and is shown to be continuous at x = 4 by evaluating the limit from the left and right and comparing it to g(4).
The x-coordinates of relative maxima of the function f on the interval [0, 3] are determined by analyzing critical points and the sign of the derivative.
A slope field for the differential equation dy/dx = y + 1/x is sketched at 12 points, indicating the slope at each point.
The solution curve for the differential equation passing through the point (-1, 0) is sketched for y > -1.
Points in the x-y plane where dy/dx equals -1 are found by setting y + 1/x equal to -1 and solving for y, resulting in a linear equation.
The slope field and solution curve illustrate the behavior of the differential equation for different values of x and y.
The process of finding limits, applying L'Hôpital's rule, and analyzing piecewise functions demonstrates the application of calculus in solving complex problems.
The transcript provides a comprehensive approach to understanding continuity, limits, and derivatives in the context of calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: