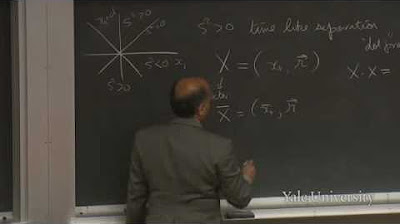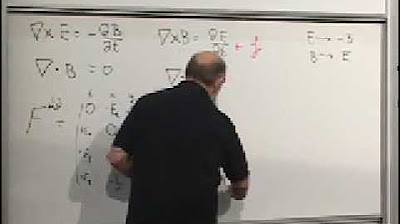Lecture 1 | Quantum Entanglements, Part 3 (Stanford)
TLDRThe provided script is a detailed lecture on the principles of special relativity, delivered by a professor from Stanford University. It begins with an introduction to the concept of relativity, emphasizing that the laws of physics remain constant across different frames of reference. The lecturer then delves into the mathematics of special relativity, carefully working through the implications of the theory, including the behavior of space and time, energy, momentum, and the influence of forces. The script outlines the thought process behind Einstein's formulation of special relativity, which was based on two postulates: the principle of relativity and the constancy of the speed of light for all observers. The lecture also touches on the Lorentz transformations, which are integral to understanding how measurements of space and time differ between moving frames of reference. The summary of the script aims to provide a clear and concise understanding of these complex topics for those interested in the foundational concepts of modern physics.
Takeaways
- 📚 The program is presented by Stanford University and covers topics on special and general relativity, with a focus on conceptual understanding rather than mathematical rigor.
- 🗓️ The lecturer will be absent for two weeks due to lectures in Israel and plans to adjust the class schedule to accommodate the missed sessions.
- 🔁 The class will continue with 10 full sessions, even if it extends into June, and there's a possibility of changing the meeting days for flexibility.
- 🕒 The concept of relativity implies that the laws of physics are the same in all frames of reference, a principle that dates back to Galileo and was further developed by Einstein.
- 🚄 Galileo's idea of relativity is demonstrated by the example of juggling on a moving train, showing that the laws of physics, such as timing and gravity, remain consistent regardless of the motion of the observer.
- ⏱️ The notion of time being absolute, as believed in Newtonian physics, was challenged by Einstein's special relativity, where time is relative and depends on the observer's motion.
- 🌌 In special relativity, the transformation of space and time coordinates leads to the conclusion that simultaneity is relative, not absolute.
- 🔄 The Lorentz Transformations, which are crucial to special relativity, ensure that the speed of light is the same in all frames of reference and that the coordinate relationships between frames are reciprocal.
- ⚖️ The principle of invariant mass is a key aspect of Newtonian physics and implies that mass is constant across all frames of reference.
- 🌟 The speed of light is a universal constant in special relativity, and this has profound implications for our understanding of space, time, and simultaneity.
- 📈 The script discusses the mathematical derivation of the Lorentz Transformations and how they lead to phenomena such as time dilation and length contraction, which are significant when dealing with velocities接近 the speed of light.
Q & A
What is the primary focus of the program discussed in the transcript?
-The program focuses on the concept of relativity, primarily special relativity, and touches upon general relativity. It aims to explore these concepts with a mix of conceptual and mathematical rigor.
Why does the lecturer mention being gone for two weeks?
-The lecturer is going to Israel to give lectures to an organization of philosophers. This affects the class schedule, which may need to be adjusted to accommodate his absence.
What is the significance of the 'Hof lecture' mentioned in the transcript?
-The 'Hof lecture' is an event that the lecturer is hosting and attending. It is significant because it conflicts with the regular class schedule, and the lecturer suggests it might not count as a regular class.
How does the lecturer plan to handle the class schedule adjustments?
-The lecturer suggests that if there is enough flexibility, they could meet on a different day of the week, such as Wednesday instead of Monday. They also consider starting the class earlier, at 6 PM instead of 7 PM, to manage the schedule.
What is the lecturer's approach to teaching special relativity?
-The lecturer plans to teach special relativity by carefully working through the mathematics, focusing on the details of space and time, and the principles of energy and momentum. They aim to cover kinematics and dynamics within the special relativity framework.
What is the basic postulate of special relativity that the lecturer refers to?
-The basic postulate of special relativity, as referred to by the lecturer, is that the laws of physics are the same in every frame of reference and that the speed of light is constant in all frames of reference.
What is the principle of Galilean relativity?
-Galilean relativity is based on the idea that the laws of physics, such as the laws of motion, are the same for all observers in uniform motion relative to one another. It assumes that time is absolute and that the speed of light could vary depending on the observer's motion.
How does the lecturer address the concept of invariants in physics?
-The lecturer discusses invariants as quantities that all observers agree upon, regardless of their frame of reference. They give examples such as the distance between two simultaneous events and the acceleration of an object, which are invariant in Galilean relativity.
What is the role of the speed of light in the development of special relativity?
-The speed of light plays a crucial role in special relativity. The lecturer emphasizes that the postulate of the constancy of the speed of light in all reference frames leads to a reevaluation of concepts like simultaneity and the transformation of space and time coordinates.
What is the Lorentz transformation?
-The Lorentz transformation is a set of mathematical equations that describe how space and time coordinates transform from one inertial frame of reference to another. It is a key element in special relativity and ensures that the speed of light is the same in all inertial frames.
Why is the concept of simultaneity considered relative in special relativity?
-The concept of simultaneity is considered relative in special relativity because the synchronization of distant clocks using light signals can lead to different observations depending on the relative motion of the observers. This challenges the classical notion of absolute simultaneity.
What are the implications of the lecturer's discussion on the speed of light for the understanding of space and time?
-The implications are profound. If the speed of light is constant for all observers, regardless of their motion, this leads to the conclusion that space and time are not absolute but are relative and can dilate and contract depending on the observer's motion, which is a fundamental aspect of special relativity.
Outlines
😀 Introduction to the Course and Relativity
The speaker introduces the course on relativity, mentioning it will cover special relativity primarily with some general relativity. They discuss the conceptual approach to the subject, acknowledging the need to adjust the schedule due to an upcoming trip to Israel for lectures. The commitment to completing the course is emphasized, even if it extends into June. The lecturer also addresses a potential scheduling conflict with the Hof lecture series and proposes an earlier class time as a solution.
📚 Detailed Exploration of Special Relativity
The lecturer outlines the plan to delve into the mathematics of special relativity, including the concepts of space, time, and SpaceTime. They emphasize the importance of understanding the symmetries and transformations. The discussion will progress to kinematics, examining how objects move without delving into the reasons behind their motion. The lecturer also plans to cover the dynamics of special relativity, including energy, momentum, and forces. The goal is to address intriguing phenomena such as black holes and the expansion of the universe.
🚂 Galileo's Relativity and Transformation of Coordinates
The paragraph explores Galileo's concept of relativity, which is based on the idea that the laws of physics remain the same in different frames of reference. The lecturer uses the analogy of juggling on a moving train to illustrate this principle. They discuss the transformation of coordinates from one frame of reference to another, emphasizing that time remains constant while spatial coordinates change, leading to the basic mathematics of Galilean relativity.
🕰️ Time, Synchronization, and Galilean Relativity
The lecturer delves into the concept of time in Galilean relativity, discussing the belief in a universal time that is unaffected by motion. They explore the idea of synchronizing clocks in a moving frame of reference and how this concept is challenged when considering the physics of a moving train. The paragraph also touches on the invariance of certain quantities, such as the distance between two simultaneous events, and how these ideas laid the groundwork for the development of relativity.
🧮 Galilean Transformations and Invariants
The paragraph focuses on the mathematical aspects of Galilean transformations, which describe how quantities like time and position change from one frame of reference to another. The lecturer discusses the invariant nature of certain physical quantities, such as the acceleration of objects, which is the same for all observers. They also touch on the concept of force and how it is perceived invariantly, leading to the formulation of Newton's second law of motion.
🌌 The Clash with Electromagnetism and Einstein's Postulates
The lecturer discusses the conflict that arises when applying Galilean relativity to the laws of electromagnetism, specifically the propagation of light. They highlight that the principle of Galilean relativity leads to a contradiction when considering the constant speed of light, as predicted by Maxwell's equations. The paragraph introduces Einstein's postulates, which assume the same laws of physics in all frames and a constant speed of light, challenging the traditional concept of simultaneity.
🔄 Synchronization and the Relativity of Simultaneity
The paragraph explores the concept of synchronizing clocks using light signals and how this process reveals the relativity of simultaneity. The lecturer explains that while clocks can be synchronized in a stationary frame of reference, a moving observer will perceive a different simultaneity due to the additional distance light must travel. This insight is crucial for the development of the Lorentz transformations, which will be discussed in the next part of the lecture.
🔶 Light Rays and the Surface of Simultaneity
The lecturer continues the discussion on the relativity of simultaneity by examining the paths of light rays and their intersections. They illustrate how the surface of simultaneity is tilted differently in a moving frame of reference compared to a stationary one. The paragraph also introduces the concept of using light to define simultaneity and how this leads to a quantitative understanding of the differences in simultaneity between two frames of reference.
🔄 Derivation of the Lorentz Transformations
The paragraph is dedicated to deriving the Lorentz transformations, which describe the relationship between two frames of reference moving at a constant velocity relative to each other. The lecturer uses geometrical constructions and algebra to find the equations that relate the space and time coordinates of an event in one frame to those in the other frame. They emphasize the importance of the speed of light being constant in all frames and how this leads to a unique set of transformation equations.
🌟 The Speed of Light and Coordinate Transformations
The lecturer discusses the implications of setting the speed of light equal to one for simplifying calculations and the importance of restoring dimensions to the equations for practical use. They also demonstrate that light moves at the same speed in both the stationary and moving frames of reference according to the derived Lorentz transformations. The paragraph concludes with a confirmation that the Lorentz transformations ensure the constancy of the speed of light for all observers.
📜 Conclusion and Future Topics
The lecturer concludes the current session by summarizing the key points discussed, including the derivation of the Lorentz transformations and the constancy of the speed of light. They outline the topics for the next class, which will include the effects of length contraction, time dilation, and further exploration of the kinematics of special relativity. The lecturer invites questions from the audience about the presented material and provides a preview of the upcoming class schedule.
🎓 Copyright and Closing
The final paragraph is a standard closing statement, indicating that the content of the program is copyrighted by Stanford University. It encourages viewers to visit the university's website for more information.
Mindmap
Keywords
💡Relativity
💡Special Relativity
💡General Relativity
💡Frame of Reference
💡Spacetime
💡Invariant
💡Galilean Relativity
💡Lorentz Transformations
💡Simultaneity
💡Speed of Light
💡Newton's Laws of Motion
Highlights
The program is introduced as being brought to you by Stanford University, emphasizing the academic prestige associated with the content.
The lecture focuses on the concept of relativity, with an emphasis on special relativity and a brief introduction to general relativity.
The speaker announces a two-week absence due to lectures in Israel, highlighting the international学术交流 (academic exchange).
The commitment to delivering ten full classes is mentioned, even if it requires extending into June, demonstrating dedication to the course completion.
The potential for adjusting class schedules to accommodate conflicts is discussed, showing flexibility in the educational approach.
The lecture outlines the structure of the course, beginning with special relativity and moving on to dynamics and general relativity.
The concept of a gravitational field in general relativity is introduced, without delving deep into Einstein's field equations.
The speaker expresses the intention to discuss complex topics such as black holes and the expansion of the universe, piquing interest in advanced physical phenomena.
The principle of relativity is explored, stating that the laws of physics are independent of the frame of reference.
Galileo's contribution to the concept of relativity is acknowledged, providing historical context to the theory's development.
The idea of Galilean relativity and its limitations are discussed, setting the stage for the need for special relativity.
The mathematical foundation of Galilean transformations is explained, providing a basis for understanding coordinate systems in physics.
The invariance of acceleration under Galilean transformations is noted, which is crucial for the formulation of Newton's laws of motion.
The conflict between Galilean relativity and Maxwell's equations is highlighted, leading to the development of special relativity.
Einstein's postulates for special relativity are presented, including the constancy of the speed of light in all inertial frames.
The concept of simultaneity is challenged, leading to the development of the Lorentz transformations.
The Lorentz transformations are derived, showing how they ensure the constancy of the speed of light and reciprocal relationships between frames.
The implications of the Lorentz transformations for the understanding of time and space are discussed, introducing key concepts of special relativity.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: