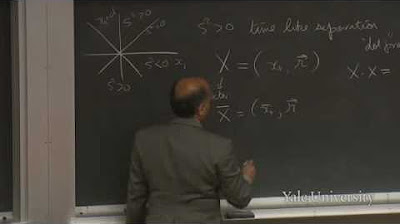Special Relativity | Lecture 2
TLDRThe video script is a detailed lecture on the fundamentals of special relativity, as taught at Stanford University. It begins with a discussion on the Lorentz transformations, which relate the coordinates of two observers moving relative to each other along a single axis. The lecturer emphasizes the constancy of the speed of light for all observers, a key postulate of Einstein's theory. The script delves into the concept of proper time and distance, explaining that these quantities are invariant across all reference frames. It also explores the addition of velocities in different frames, highlighting that the resultant velocity cannot exceed the speed of light. The lecture further introduces the idea of four-vectors and four-velocity, which are essential for understanding the motion of particles in relativistic physics. The script concludes with a mention of the light cone, a concept that illustrates the paths that light can take from a single point in space-time. The lecture is rich with mathematical insights and thought experiments designed to help students grasp the often counterintuitive principles of special relativity.
Takeaways
- 📐 **Lorentz Transformations**: The script discusses Lorentz transformations, which relate the space and time coordinates of events as observed in two different inertial frames of reference moving relative to each other.
- 🚄 **One-Dimensional Motion**: Initially, the focus is on one-dimensional motion along a single axis, with stationary observers at a station and moving observers on a train.
- 🌟 **Speed of Light**: Einstein's basic hypothesis is that the speed of light is observed as the same by all reference frames, which simplifies equations when the speed of light is set to one.
- 🔄 **Reciprocal Relations**: The Lorentz transformations are reciprocal, allowing the coordinates of one observer to be related to the other, with a sign change in velocity reflecting the direction of movement.
- 🚂 **Third Observer Scenario**: The script introduces a scenario with a third observer moving within the train (kiddy car) and discusses how to calculate the relative velocity (W) of this observer to the stationary observer on the platform.
- 🧮 **Combining Velocities**: The script explores the addition of velocities in relative motion, emphasizing that even at high speeds, the combined velocity cannot exceed the speed of light.
- 🕰️ **Proper Time and Interval**: The concept of proper time (τ) is introduced as an invariant interval between two events in space-time, which is the same for all observers regardless of their relative motion.
- 📏 **Space-Time Coordinates**: The script extends the discussion to include y and z coordinates, highlighting that rotations and Lorentz transformations can be applied to these additional dimensions without changing the invariant nature of the proper interval.
- 🛤️ **Light Cones**: The script describes the path of light rays in space-time, illustrating how they form a light cone, which represents all points that light can reach from a given point (the future light cone) or all points that can send light to a given point (the past light cone).
- 🧲 **Four-Vector**: The script introduces the concept of a four-vector, which includes three spatial components and one time component, and how these transform under Lorentz transformations.
- 🌀 **Four-Velocity**: The script discusses the notion of four-dimensional velocity, which is different from ordinary velocity and is defined using the invariant space-time distance (Δτ) between two points.
Q & A
What is the basic concept of Lorentz transformations?
-Lorentz transformations are mathematical equations that relate the space and time coordinates of an event as observed in two different inertial reference frames, which are moving at a constant velocity relative to each other.
How does the speed of light relate to Lorentz transformations?
-The speed of light is a fundamental constant in Lorentz transformations, with the assumption that all observers, regardless of their relative motion, measure the speed of light to be the same. This leads to the time dilation and length contraction effects in special relativity.
What is the significance of the term 'proper time' in the context of special relativity?
-Proper time (τ) is the time interval between two events as measured by a clock that is at rest with respect to the events. It is an invariant quantity, meaning all observers, regardless of their relative motion, agree on the value of the proper time between two events.
How does the concept of a 'light cone' relate to the motion of light rays?
-A light cone represents the set of all points in space-time that can be reached by a light ray originating from a given point. It is formed by the worldlines of light rays moving at 45-degree angles to the time and space axes, indicating all possible future (and past) positions reachable by light from a specific event.
What is the role of the speed of light (c) in the equations of special relativity?
-The speed of light (c) is a key factor in the equations of special relativity. It is often set to a value of 1 in natural units to simplify the equations. When considering real-world measurements, the speed of light is reintroduced to maintain dimensional consistency.
How does the relative velocity between two observers affect their measurements?
-The relative velocity between two observers affects their measurements of space and time due to the Lorentz transformations. Observers moving relative to each other will measure different lengths (length contraction) and durations of time (time dilation) for the same events.
What is the four-vector notation used in special relativity?
-The four-vector notation in special relativity is a way of organizing space-time coordinates into a single mathematical object with four components. It is typically denoted as X^μ, where μ (mu) runs from 0 to 3, with 0 representing time (t) and 1 to 3 representing the spatial coordinates (x, y, z).
How does the concept of four-velocity differ from the ordinary three-dimensional velocity?
-Four-velocity is a four-dimensional generalization of the velocity that includes time as an additional dimension. It is defined as the rate of change of the four-position with respect to the proper time. Unlike three-dimensional velocity, four-velocity is always time-like and its magnitude is the speed of light in natural units.
What is the invariant interval in special relativity?
-The invariant interval in special relativity is the space-time distance between two events, given by the square root of (ΔT^2 - ΔX^2 - ΔY^2 - ΔZ^2), where ΔT, ΔX, ΔY, and ΔZ are the differences in time and space coordinates of the two events. This interval is the same for all observers, regardless of their relative motion.
How does the addition of velocities in special relativity differ from classical mechanics?
-In special relativity, the addition of velocities cannot exceed the speed of light. When adding two velocities (u and v), the resulting velocity (w) is given by w = (u + v) / (1 + uv/c^2), where c is the speed of light. This equation ensures that as the velocities approach the speed of light, the combined velocity also approaches, but never exceeds, the speed of light.
What is the significance of the term 'simultaneity' in the context of special relativity?
-In special relativity, simultaneity is relative, meaning that two events that are simultaneous in one frame of reference may not be simultaneous in another frame that is moving relative to the first. This is due to the time dilation effect, which causes time to pass at different rates for observers in relative motion.
Outlines
📐 Introduction to Lorentz Transformations
The paragraph introduces the concept of Lorentz transformations, which relate the coordinates of different observers moving relative to each other along a single axis. It discusses the scenario of a stationary observer at a train station and another observer in a moving train. The focus is on how these observers can relate their coordinates to each other using the Lorentz transformations, which are based on the postulate that the speed of light is constant across all frames of reference.
🚉 Observers' Relative Motion and Lorentz Transformations
This section delves deeper into the Lorentz transformations, providing the mathematical relationships between the space and time coordinates (X, T) of a stationary observer and (X', T') of a moving observer. It explains how these transformations ensure that the speed of light is observed as constant (set to 1 in the chosen units) by all observers. The paragraph also touches on the concept of reciprocity in these transformations and the sign change of velocity when considering the reverse observation.
🧭 Incorporating a Third Observer and Relative Velocities
The script introduces a third observer moving within the train, relative to the passenger, and inquires about the velocity (W) as seen by the stationary observer. It outlines the logical steps to determine W in terms of U (velocity of the car relative to the train) and V (velocity of the train relative to the stationary observer). The paragraph establishes the need for additional Lorentz transformations to relate the coordinates of the three different observers.
🔗 Deriving the Relative Velocity of the Third Observer
The paragraph focuses on deriving the relative velocity (W) of the third observer (in the kiddie car) with respect to the stationary observer at the train station. It uses the Lorentz transformation equations and the concept of invariant space-time intervals to express W in terms of U and V. The result is an equation that shows how the velocities add up relativistically, rather than simply as in classical mechanics.
🌟 The Speed of Light and Its Implications
This section discusses the implications of adding velocities in the context of the speed of light. It contrasts the Newtonian approach, which would naively add velocities, with the relativistic approach, which includes a corrective factor. The paragraph provides examples to illustrate how the addition of velocities works in both scenarios where the velocities are much smaller and close to the speed of light, emphasizing that no observer can exceed the speed of light relative to a stationary frame.
⏱️ Proper Time and Space-Time Intervals
The paragraph introduces the concept of proper time (tau), which is the time measured by a clock moving between two points in space-time. It explains that proper time is an invariant quantity, meaning all observers agree on its value regardless of their relative motion. The paragraph also generalizes the notion of space-time intervals to include additional spatial dimensions (Y and Z), leading to the concept of an invariant interval in any inertial frame.
📐 Transformation Laws and Universality
The script emphasizes the universality of transformation laws in special relativity, stating that these laws apply regardless of the physical properties of the objects involved, such as the walls of a train car. It then transitions into a discussion about the concept of four-vectors, which are essential for describing the motion of particles in a relativistic context. The paragraph outlines the basic properties of four-vectors and their transformation under Lorentz transformations.
🚀 Four-Velocity and Its Relation to Ordinary Velocity
The final paragraph introduces the concept of four-velocity, which is a generalization of the ordinary three-dimensional velocity to include time as a component. It explains how four-velocity is calculated using the space-time interval (Delta Tau) between two points on a particle's trajectory. The paragraph sets the stage for a deeper exploration of the dynamics of particles in the context of special relativity, hinting at the generalization of Newton's laws to four-dimensional space-time.
Mindmap
Keywords
💡Lorentz Transformations
💡Speed of Light
💡Reference Frames
💡Space-Time
💡Proper Time
💡Light Cone
💡Four-Vector
💡Time Dilation
💡Invariant Interval
💡Relative Velocity
💡Simultaneity
Highlights
Introduction to Lorentz transformations and their relation to the speed of light in the context of different reference frames.
Explanation of how the speed of light is perceived as constant (equal to one) in all reference frames, simplifying equations.
Discussion on the symmetry of motion and how it relates to the Lorentz transformations between stationary and moving observers.
Illustration of how to apply Lorentz transformations to calculate coordinates in different frames of reference.
Introduction of the concept of a 'light cone' representing the set of points that a light ray can reach from a given point in space-time.
Explanation of how the relative velocity between two observers (W) can be determined using Lorentz transformations.
Demonstration of how to calculate the invariant proper time interval (tau) between two events in different reference frames.
Clarification that the proper time interval is the same for all observers, regardless of their relative motion.
Introduction of the concept of four-vectors and their significance in special relativity.
Explanation of how four-vectors transform under Lorentz transformations, similar to how vectors transform under rotations.
Discussion on the four-dimensional velocity, also known as four-velocity, and its relation to the invariant space-time distance.
Introduction of the concept of 'proper distance' and how it is different from the ordinary Euclidean distance.
Explanation of how the speed of light is measured in different moving frames and the consistency of its value.
Discussion on the relativistic addition of velocities and how it differs from simple Newtonian addition.
Use of matrices to simplify the application of Lorentz transformations to four-vectors.
Introduction of the concept of simultaneity and how it is affected by the relative motion of observers.
Explanation of how the future and past light cones are defined and their significance in the context of causality.
Discussion on the generalization of Newtonian mechanics to special relativity, including the concept of four-acceleration.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: