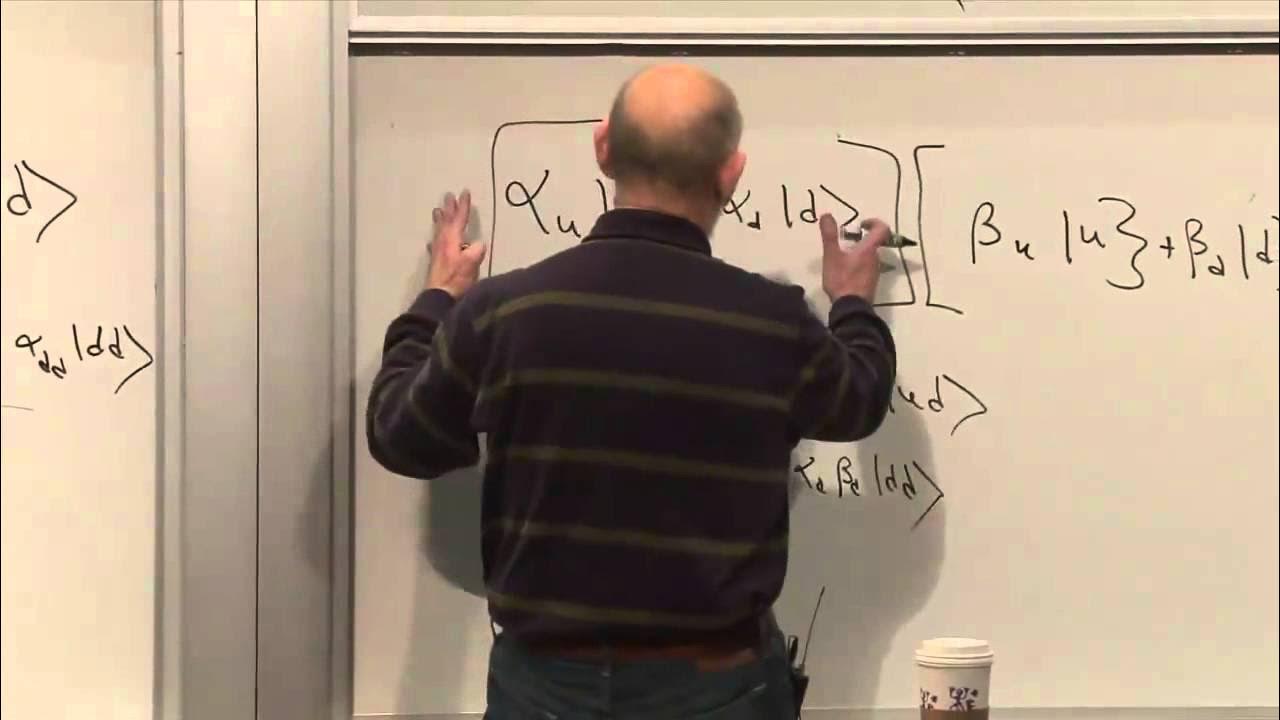Lecture 5 | The Theoretical Minimum
TLDRThe transcript appears to be a lecture on quantum mechanics, focusing on the Schrödinger equation, the concept of uncertainty, and the behavior of a single spin in a magnetic field. The lecturer delves into the time evolution of quantum systems, explaining how states change over time through the Schrödinger equation, which is fundamental to quantum mechanics. The uncertainty principle is discussed, highlighting that certain pairs of observables cannot be simultaneously measured with precision. The lecture also explores the Hamiltonian operator, its role in generating time evolution, and its relationship with energy in a quantum system. The讲师 (lecturer) uses the example of a spin in a magnetic field to illustrate these concepts, discussing the Hamiltonian for such a system and how it leads to the precession of the spin vector. The commutation relations of the sigma matrices are worked out, and the lecturer shows how these relations lead to the equations of motion for the spin components. The lecture concludes with a discussion on the emission of photons by spins in magnetic fields, the probabilities involved, and the behavior of quantum systems under observation.
Takeaways
- 📚 The lecture discusses the concept of uncertainty in quantum mechanics, highlighting that certain pairs of observables cannot be simultaneously measured with precision.
- 🌟 The Heisenberg Uncertainty Principle is mentioned, which states that the more precisely the position of a particle is determined, the less precisely its momentum can be known, and vice versa.
- 🧵 The lecture touches on the Schrödinger equation, which describes how quantum systems evolve over time, and its different versions for various scenarios.
- ⏱️ Time evolution of states is a key topic, with the Schrödinger equation providing a rule for updating the state of a quantum system incrementally.
- 🚫 It is emphasized that measurements in quantum mechanics disturb the system, which is in contrast to classical mechanics where the state can be observed without significant disturbance.
- 🌀 The general solution to the Schrödinger equation is explored, explaining how the coefficients of state vectors change over time, leading to time-dependent expectation values.
- 📈 The expectation value of an observable is calculated using the state vector and its complex conjugate, with the Hamiltonian operator playing a crucial role in determining the time evolution of these values.
- 🤔 The lecture ponders the question of why the magnetic field is not treated as an operator in quantum mechanics, delving into the distinction between quantum systems and classical apparatuses.
- 🧲 The example of a spin in a magnetic field is used to illustrate the calculation of time derivatives of spin components, leading to the understanding of how spin precesses in a magnetic field.
- 🤷♂️ The role of probability and statistics in quantum mechanics is acknowledged, with the lecturer expressing the puzzling nature of why probability works in the context of quantum phenomena.
- ✨ The emission of a photon by an electron in a magnetic field is discussed, noting that the process is probabilistic and the electron may either emit a photon or not, depending on its state.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is quantum mechanics, specifically focusing on the Schrödinger equation, the concept of uncertainty, and the evolution of quantum systems over time.
What is the significance of the Schrödinger equation in quantum mechanics?
-The Schrödinger equation is significant in quantum mechanics as it governs the time evolution of quantum systems. It is used to predict how quantum states change over time and is fundamental to understanding quantum behavior.
What is the concept of uncertainty in quantum mechanics?
-The concept of uncertainty in quantum mechanics refers to the principle that certain pairs of observables, like position and momentum, cannot be simultaneously measured to arbitrary precision. This is often referred to as Heisenberg's Uncertainty Principle.
How does the Hamiltonian operator relate to the energy of a system in quantum mechanics?
-In quantum mechanics, the Hamiltonian operator represents the total energy of a system. It is a Hermitian operator, and its eigenvalues correspond to the possible energy levels of the system.
What is the role of the commutator in quantum mechanics?
-The commutator plays a crucial role in quantum mechanics as it helps determine whether two observables can be simultaneously measured. If the commutator of two operators is zero, it indicates that the observables commute and can be measured at the same time.
How does the time evolution of a quantum state affect the expectation values of observables?
-The time evolution of a quantum state, governed by the Schrödinger equation, affects the expectation values of observables through the change in the state's coefficients. These changes can lead to variations in the expectation values over time.
What is entanglement in the context of quantum mechanics?
-Entanglement is a phenomenon in quantum mechanics where the states of two or more particles become correlated in such a way that the state of one particle cannot be described independently of the state of the other particles, even when the particles are separated by large distances.
What does the speaker mean by 'the next to next simplest system' in the context of quantum mechanics?
-The speaker is referring to the complexity of quantum systems. After the simplest system, which is a single spin with two states, the next simplest system would be a system with three states. However, the speaker mentions that the 'next to next simplest system' is one with two spins, which has more complexity due to the increased number of states resulting from the combination of the two spins.
Why does the Hamiltonian operator need to be Hermitian in quantum mechanics?
-The Hamiltonian operator needs to be Hermitian to ensure that its eigenvalues, which represent the possible energy levels of a quantum system, are real numbers. This is important because the probabilities in quantum mechanics, which are derived from these eigenvalues, must be real and positive.
What is the significance of the speaker's discussion about the measurement process in quantum mechanics?
-The speaker's discussion about the measurement process is significant because it highlights the fundamental differences between classical and quantum mechanics. In quantum mechanics, the act of measurement disturbs the system and can change its state. This is in contrast to classical mechanics, where measurement does not necessarily affect the system's state.
How does the speaker describe the evolution of a quantum system that is not being measured?
-The speaker describes the evolution of an undisturbed quantum system, one that is not being measured, as deterministic in a sense. The state vector of the system evolves in a known and definite way according to the Schrödinger equation. However, this evolution is probabilistic, as the knowledge of the state does not guarantee the outcome of every possible measurement.
Outlines
📚 Introduction to Quantum Mechanics Concepts
The first paragraph introduces the topics to be covered in the lecture, including uncertainty, the Schrödinger equation, and the evolution of quantum systems over time. It emphasizes the general principles of quantum mechanics, such as the role of observables and states, and the concept of distinguishable states. The lecture also hints at exploring systems with multiple spins, highlighting the complexity of states as they increase from single to multiple entities.
🌟 Uncertainty Principle and Observables
The second paragraph delves into the uncertainty principle, discussing how certain pairs of observables cannot be simultaneously measured with precision. It explains the conditions under which observables can be simultaneously measured—namely, when the operators representing these observables commute. The concept of a basis of vectors, which are simultaneous eigenvectors of distinct observables, is also explored, leading to the theorem that commuting observables allow for simultaneous measurability.
🚫 Non-commuting Operators and Uncertainty
The third paragraph contrasts the conditions for simultaneous measurability with the behavior of operators that do not commute, such as the Pauli spin matrices. It reinforces the idea that non-commuting operators cannot be simultaneously measured, which is a core aspect of the uncertainty principle. The paragraph also touches on the classical physics perspective, where observables like position and momentum can be known with certainty, unlike in quantum mechanics.
🕰 Time Evolution of Quantum States
The fourth paragraph discusses the time evolution of quantum states, focusing on the Schrödinger equation's role in governing this process. It covers the conservation of orthogonality in states and the U operator, which projects a state from an initial time to a later time. The concept of continuity in state evolution is introduced, leading to the derivation of the Hamiltonian as a Hermitian operator, which is crucial for the deterministic evolution of quantum states.
⚙️ The Hamiltonian and Quantum Determinism
The fifth paragraph examines the Hamiltonian in more detail, emphasizing its role in the deterministic evolution of a quantum system when no measurements are being made. It distinguishes between the deterministic evolution of the state vector and the probabilistic nature of measurement outcomes. The Hamiltonian is identified as a generator of time evolution, and its hermiticity is linked to the conservation of probability.
🌀 Evolution of Expectation Values
The sixth paragraph explores the evolution of expectation values over time. It explains how the state vector's time dependence leads to changes in expectation values and how these changes can be computed using the time-dependent Schrödinger equation. The paragraph also introduces the concept of the Heisenberg picture of quantum mechanics, where the observables evolve while the states remain constant.
🔍 Commutators and the Heisenberg Equations
The seventh paragraph focuses on commutators and their significance in quantum mechanics. It establishes the rules for commutators, drawing parallels with the rules for Poisson brackets from classical mechanics. The paragraph also introduces the Heisenberg equations of motion, which describe how the average values of observables change over time, and highlights the importance of commutators in these equations.
🧲 Spin in a Magnetic Field
The eighth paragraph applies the concepts discussed to a practical scenario: a single spin in a magnetic field. It outlines the Hamiltonian for a spin in a magnetic field, derives the time evolution of the spin components, and explains how the spin precesses around the magnetic field direction. The solution to the Schrödinger equation for this system is presented, illustrating how expectation values of spin components change over time.
🤔 Quantum Mechanics and Classical Limit
The ninth paragraph contemplates the brittleness of quantum mechanics as a theory and contrasts it with other physical theories that allow for more deformation. It also addresses questions about the real numbers in quantum states, the unitarity of the Hamiltonian, and the connection between quantum mechanics and classical mechanics. The paragraph ends with a discussion on the probabilistic nature of quantum mechanics and its experimental validation.
🔄 Precession of Spin and Angular Momentum
The tenth paragraph further explores the precession of a quantum spin in a magnetic field, drawing analogies with classical angular momentum. It discusses the relationship between the spin operators and their commutation relations, which are reminiscent of the Poisson brackets for angular momentum. The paragraph also touches on the cyclic nature of these commutation relations and their implications for the dynamics of spin.
🧲 General Hamiltonian for a Single Spin
The eleventh paragraph discusses the most general form of the Hamiltonian for a single spin system. It explains that the Hamiltonian can be a linear combination of the Pauli matrices and that adding a magnetic field in any direction results in the spin precession around that direction. The paragraph also addresses questions about the dimensionality of state spaces and the relationship between real space and state space vectors.
🤔 Quantum Measurement and Apparatus
The twelfth paragraph ponders why the magnetic field is treated classically rather than as a quantum operator. It discusses the division between the quantum system and the measurement apparatus, and the justification for treating heavy objects like magnets classically due to their minimal quantum fluctuations. The paragraph also raises questions about the nature of quantum measurement and the probabilistic outcomes of quantum events.
📡 Emission of Photons by a Spin
The final paragraph addresses the possibility of a quantum spin emitting a photon when in a magnetic field. It explains that while the spin can undergo transitions between energy states, the probability of emitting a photon per unit time can be very small, leading to a spin that precesses many times before a photon is emitted. The paragraph concludes with a discussion on the probabilistic nature of quantum mechanics and the role of statistics in understanding experimental outcomes.
Mindmap
Keywords
💡Uncertainty Principle
💡Schrodinger Equation
💡Observables
💡Eigenvalues and Eigenvectors
💡Hamiltonian
💡Spin
💡
💡Commutator
💡Hermitian Operator
💡Time Evolution
💡Entanglement
💡Magnetic Field
Highlights
Discussion on uncertainty and the Heisenberg equation, emphasizing the impossibility of simultaneously measuring certain pairs of observables.
Exploration of the time evolution of quantum systems through the Schrödinger equation and its implications for state vectors.
Introduction to the concept of Hermitian operators and their role in quantum mechanics, particularly in relation to observables and states.
Explanation of how orthogonal vectors signify distinguishable states in quantum mechanics.
Application of quantum mechanical principles to the simplest systems, such as a single spin, and the progression to more complex systems like two spins.
Elaboration on the mathematical framework of quantum mechanics, including the use of bra-ket notation and the importance of linear independence in quantum states.
Discussion on the measurement process in quantum mechanics and how it affects the state of a system, introducing the concept of eigenstates and eigenvalues.
Derivation of the Heisenberg Uncertainty Principle from the properties of commutators and the conditions for simultaneous measurability of observables.
Analysis of the Hamiltonian operator as a generator of time evolution in quantum systems, and its significance in determining the dynamics of a system.
Presentation of the time-dependent Schrödinger equation and its role in describing how quantum states change over time.
Calculation of expectation values and the introduction of the concept of the Heisenberg picture of quantum mechanics.
Illustration of how the Hamiltonian operator, when applied in sequence with other observables, affects the state of a quantum system.
Discussion on the conservation of energy in quantum mechanics and the role of the Hamiltonian in this principle.
Investigation of the commutation relations of the spin operators and their implications for the dynamics of a quantum spin in a magnetic field.
Solution to the problem of a single spin in a magnetic field, demonstrating how the average values of the spin components change over time.
Theoretical prediction that a spin in a magnetic field will precess around the magnetic field direction, analogous to classical gyroscopic precession.
Explanation of the quantum mechanical process of a spin system emitting a photon when transitioning between energy levels.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: