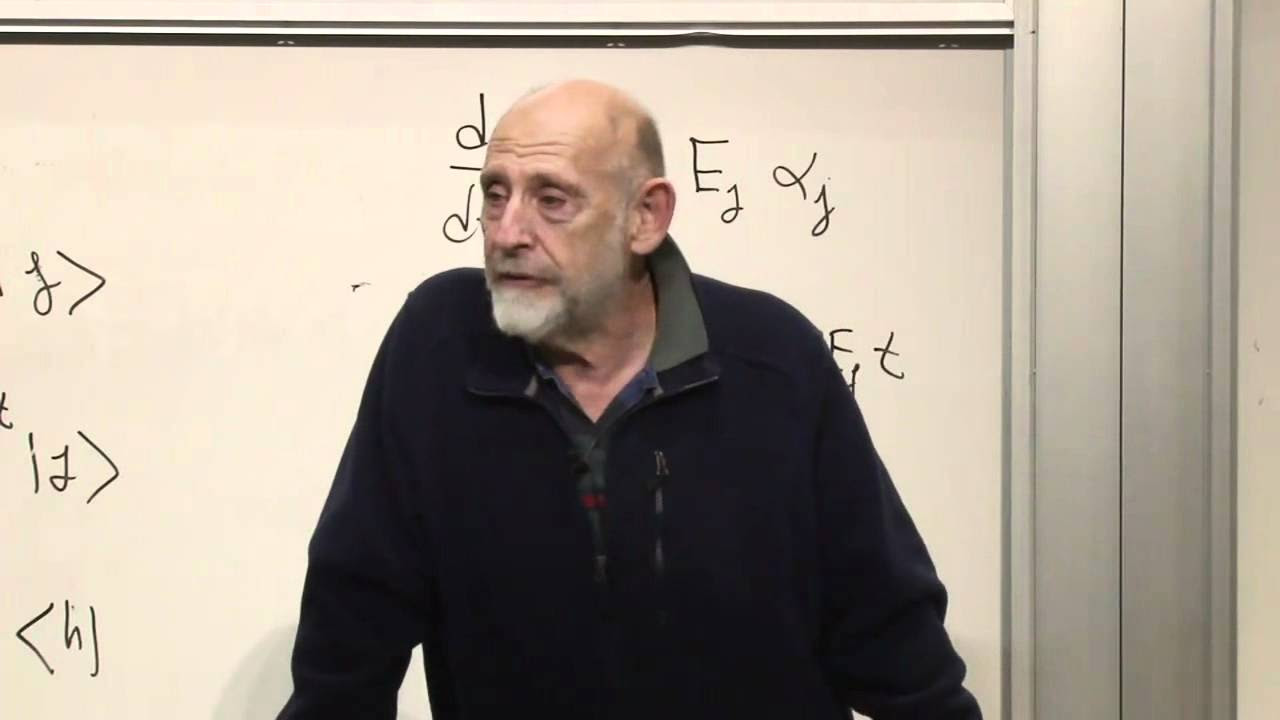Lecture 6 | The Theoretical Minimum
TLDRThe video script is a detailed lecture on quantum mechanics, specifically focusing on the concept of spin in a magnetic field and the phenomenon of quantum entanglement. The lecturer clarifies a student's question about a system emitting a photon when in a superposition of energy states, explaining that the energy of the emitted photon corresponds to the difference between the two energy levels. The discussion then transitions into the behavior of a quantum system when measured, touching on the collapse of the wave function and the difference between the evolution of quantum states via the Schrödinger equation and the outcome of measurements. The lecturer delves into the intricacies of entanglement, using the example of two spins to illustrate how their states cannot be described independently once they have interacted, leading to a statistical correlation that is indicative of entanglement. The script challenges classical intuitions and highlights the unique and non-classical nature of quantum mechanical systems.
Takeaways
- 📚 The lecture discusses quantum mechanics, specifically focusing on the behavior of spins in a magnetic field and the concept of entanglement.
- 🌀 When a spin system emits a photon, it transitions from a higher energy state to a lower one, with the photon's energy matching the difference between the two states.
- 🎓 The Hamiltonian, represented as Ω/2Σz, is used to describe the energy states of a spin system, with two possible energy levels, E1 (-Ω/2) and E2 (+Ω/2).
- 🚫 A spin system cannot emit a photon from a lower energy state as it lacks the necessary energy to do so.
- 🤔 The probability of a spin system emitting a photon depends on its initial state, which can be a superposition of up and down states, represented by α and β coefficients.
- 🧲 The energy emitted through radiation, when a classical spinning object precesses in a magnetic field, is dependent on the angle of orientation and follows a continuous spectrum.
- 💡 Quantum mechanically, a system can only emit a photon with a specific energy, which is discrete and not continuous as in the classical case.
- 🌟 The concept of wave function collapse is introduced, where upon measurement, the system ends up in a definite state corresponding to the observable's eigenvalue.
- 🔬 The lecture touches on the idea of nonlocality in quantum mechanics, suggesting that entangled particles behave in ways that cannot be explained by classical physics alone.
- 🤝 Entangled states, such as the singlet state described (up, down - down, up), have properties where measuring one particle immediately defines the state of the other, regardless of distance.
- ⚖️ The expectation values of certain observables, like Σx * τx, in entangled states can be nonzero, indicating a correlation between the subsystems that is not present in product states.
Q & A
What is the significance of the Hamiltonian in the context of the discussed quantum system?
-The Hamiltonian, denoted as Omega over 2 in the script, is used to describe the total energy of the quantum system. It is particularly important when discussing the energy levels of a system in a magnetic field, as it helps define the transition between states, which is crucial for understanding phenomena such as photon emission.
What is the energy difference between the two eigenvalues (E1 and E2) in the given quantum system?
-The energy difference between the two eigenvalues (E1 and E2) is Omega. E1, the lower energy level, is at -Omega/2, and E2, the upper energy level, is at +Omega/2. This energy difference is significant as it determines the energy of the photon emitted during a transition from the upper to the lower state.
How does the probability of photon emission relate to the initial state of the system?
-The probability of photon emission is not necessarily one, meaning it is not guaranteed to occur even if the system is in an excited state. If the initial state is a superposition of states, the probability of emission is determined by the square of the coefficients of the superposition state. For instance, with probability |Alpha|^2, the system emits a photon, and with probability |Beta|^2, it does not.
What is the classical expectation value of the spin in a magnetic field?
-Classically, the energy of a spinning rotor in a magnetic field is proportional to the cosine of the angle between the axis of spin and the magnetic field. The expectation value of the spin precesses around the magnetic field with frequency Omega, and the amount of radiation emitted depends on the initial angle of the spin.
What is entanglement in quantum mechanics?
-Entanglement is a quantum phenomenon where the quantum states of two or more particles become interlinked so that the state of one particle cannot be described independently of the state of the other particles. This leads to correlations between observable physical properties of the particles, such as position, momentum, spin, etc.
How does the process of measurement affect the state of a quantum system?
-Measurement in quantum mechanics causes the wave function of a quantum system to collapse. This means that prior to measurement, the system is in a superposition of states, but upon measurement, it is found in one of the eigenstates corresponding to the observable being measured. The process is not governed by the Schrödinger equation but rather by the act of measurement itself.
What is the tensor product in the context of combining two quantum systems?
-The tensor product is a mathematical operation that combines the state spaces of two quantum systems to form a new state space for the composite system. It is used to describe the combined system when two subsystems interact. The tensor product space has basis vectors that are labeled by pairs of indices, one from each subsystem.
What is the difference between a product state and an entangled state in a two-particle quantum system?
-A product state is a state in which each particle has a well-defined state independently of the other, requiring only four real parameters to describe. An entangled state, on the other hand, cannot be described independently for each particle and requires six real parameters. Entangled states exhibit correlations between the particles that are not classically explainable.
How does the concept of superposition relate to the expectation values of spin components in a quantum state?
-In quantum mechanics, a superposition state is a linear combination of basis states. The expectation value of a spin component in a superposition state is not necessarily zero. However, for a state to be a product state, the expectation values of all three spin components cannot simultaneously be zero, as this would imply the existence of a definite direction in space for the spin, which contradicts the nature of a superposition.
What is the significance of the singlet state in the context of two interacting spins?
-The singlet state is a maximally entangled state of two spins where the total spin is zero. It is characterized by a perfect anti-correlation between the two spins, meaning that if one spin is measured to be in an up state, the other is guaranteed to be in a down state, and vice versa. This state is significant because it cannot be factored into a product state and represents a strong form of quantum entanglement.
How does the concept of entanglement entropy measure the strength of entanglement in a quantum system?
-Entanglement entropy is a measure used in quantum information theory to quantify the amount of entanglement in a quantum system. It is calculated from the reduced density matrix of a subsystem and is invariant under changes of basis. A higher entanglement entropy indicates a stronger degree of entanglement between the subsystems.
Outlines
🤔 Spin, Magnetic Fields, and Photon Emission
The paragraph discusses a question raised in a class about the behavior of a spin system in a magnetic field. It explores the concept of energy levels associated with spin states and how a transition between these states can result in photon emission. The energy of the emitted photon corresponds to the energy difference between the two states. The lecturer also addresses a hypothetical scenario where the spin is not aligned with the magnetic field but at an angle, and clarifies that the energy of the emitted photon remains the same.
🌌 Quantum Mechanics and Emission of Radiation
This section delves into the classical and quantum mechanical aspects of a spinning object in a magnetic field. It explains how the energy and radiation emitted by such an object depend on its orientation. In the quantum realm, the system can only emit photons with specific energy levels, and the probability of emission is influenced by the initial state of the system. The average energy emitted is likened to the classical energy, and the concept of a superposition of states is introduced.
📉 Wave Function Collapse and Quantum Measurements
The lecturer introduces the concept of wave function collapse during the measurement process in quantum mechanics. The wave function, which evolves according to the Schrödinger equation, is said to collapse to a definite state when a measurement is made. This collapse is not governed by the Schrödinger equation but by the nature of the measurement process itself. The lecturer also raises questions about the need for a combined system approach when considering measurements and the implications of this for quantum mechanics.
🧬 Entanglement and the Combination of Quantum Systems
The paragraph explores the idea of entanglement and the process of combining two quantum systems into one. It explains the mathematical concept of a tensor product, which is used to describe the combined state space of multiple quantum systems. The lecturer discusses the construction of a new space of states by pairing basis vectors from each individual system and emphasizes that the resulting space is independent of the chosen basis.
🔬 Tensor Product and the Space of States for Two Spins
This section provides a concrete example of the tensor product by considering two spins. The basis vectors for the combined system of two spins are outlined, and it is shown that any state in the combined system can be represented as a linear combination of these basis vectors. The paragraph also discusses how the interaction between the two spins can change the coefficients of the linear combination, but not the basis vectors themselves.
🌐 Product States and the Independence of Subsystems
The lecturer discusses product states, which are states where each subsystem can be described independently. It is explained that if experiments are conducted on only one half of a combined system, the results should match those obtained when considering the subsystem in isolation. The concept of a product state is contrasted with entangled states, where the subsystems cannot be described independently.
🔍 Observables and the Action of Spin Operators
This paragraph examines the observables for a composite quantum system made up of two spins. It explains how the spin operators for each subsystem act on the states of the combined system. The讲师 clarifies that the action of one spin's operator on the combined system only affects its corresponding spin and leaves the other unchanged. This demonstrates that the subsystems behave independently unless they interact.
🤓 Commutators and the Independence of Observables
The lecturer discusses the commutator properties of the spin operators for two separate subsystems. It is shown that the order of operations for the spin components of different subsystems does not matter, indicating that the observables for one subsystem do not interfere with the measurements of the other. This supports the idea that the subsystems can be measured independently.
🌀 Entanglement and Non-Product States
The concept of entanglement is further explored with the introduction of a maximally entangled state, which cannot be described as a product state. The lecturer explains that in an entangled state, the subsystems are correlated in such a way that the state of one subsystem directly influences the state of the other, regardless of the distance between them. This leads to the idea that entanglement is a fundamental aspect of quantum mechanics that cannot be replicated by classical reasoning.
📚 Entanglement Entropy and Invariance of Entanglement
The paragraph concludes with a discussion on the entanglement entropy, a measure of the degree of entanglement in a quantum system that is independent of the chosen basis. The lecturer confirms that entanglement is a robust concept that remains consistent across different bases, and touches on the idea that entanglement cannot be simulated by classical computers unless they are connected in a non-local manner.
Mindmap
Keywords
💡Quantum Mechanics
💡Spin
💡Magnetic Field
💡Photon
💡Energy Levels
💡Entanglement
💡Wave Function Collapse
💡Tensor Product
💡Observables
💡Superposition
💡Schrodinger Equation
Highlights
The lecturer revisits a question from the previous class about a spin in a magnetic field emitting a photon, emphasizing its importance for understanding quantum mechanics.
Discussion on the Hamiltonian setup with two energy levels, E1 and E2, and the possibility of a system emitting a photon when transitioning between these levels.
Explanation that the energy of the emitted photon corresponds to the energy difference between the upper and lower states, denoted by Ω (Omega).
Addressing a hypothetical scenario where a spin is not aligned with the magnetic field axis and the implications for photon emission energy.
Clarification that a spin pointed in an arbitrary direction will not emit a photon of half the energy (Ω/2), counter to the initial hypothetical question.
Introduction to the concept of spin precession around a magnetic field with frequency Ω, and its classical and quantum mechanical interpretations.
The lecturer explains that quantum mechanically, a system can only emit a photon with a specific energy, contrasting with classical radiation emission.
Discussion on the probability of photon emission based on the initial state of the system, and how it relates to the superposition of states.
Calculation of the average energy of the system, highlighting the difference between individual quantum events and the classical expectation.
The lecturer touches on the topic of quantum entanglement and the collapse of the wave function, a fundamental concept in quantum mechanics.
Exploration of the measurement process in quantum mechanics and how it differs from the evolution of quantum states governed by the Schrödinger equation.
Introduction of the tensor product as a method to combine the states of two quantum systems into a single quantum system.
Explanation of how to combine systems by creating a new space of states, where the basis vectors are labeled by pairs of values from each individual system.
The concept of product states within the tensor product space, and how they differ from entangled states.
Calculation of the number of parameters needed to describe a general state of a two-spin system, highlighting the difference between product and entangled states.
The lecturer provides a concrete example of two entangled spins, demonstrating the mathematical formalism behind their combined state.
Discussion on the observables for the combined system and how they relate to the individual subsystems' observables.
Explanation of the commutation relations between the components of different spins and the implications for simultaneous measurements.
The lecturer concludes with a thought experiment involving two entangled spins and the challenges of simulating quantum mechanics classically.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: