Lecture 9 | Quantum Entanglements, Part 1 (Stanford)
TLDRThe video script is an in-depth exploration of quantum mechanics, focusing on the time evolution of quantum states. It begins by discussing the description of a system's state by a ket vector and the concept of time dependence. The lecturer emphasizes the linearity of state vector changes and introduces the postulate that systems change with time through linear operators. The role of the Hamiltonian operator in governing the time evolution of quantum states is highlighted, leading to the derivation of the Schrödinger equation. The script delves into the solution of the Schrödinger equation for eigenvectors of the Hamiltonian, illustrating how these states evolve over time. The Hamiltonian's significance is further discussed in terms of observables and expectation values, with a clear explanation of the conservation of energy and the concept of degenerate energy levels. The lecturer uses the example of a spin in a magnetic field to demonstrate these principles, showing how expectation values of spin components change with time. The script concludes with a detailed analysis of a two-electron system, including the triplet and singlet states, and how their probabilities evolve over time. The summary underscores the fundamental principles of quantum mechanics, the Hamiltonian's role, and the application of these concepts to specific quantum systems.
Takeaways
- 📚 The state of a quantum system is described by a ket vector, which can be influenced by time, leading to the concept of the time-dependent Schrödinger equation.
- ⏱️ Time evolution of quantum states is governed by a linear operator, which is a postulate in quantum mechanics, ensuring probability conservation.
- 📐 The Hamiltonian operator, denoted by 'H', is a Hermitian operator that represents the total energy of the system and is fundamental to describing how quantum states change over time.
- 🌀 The Schrödinger equation is a differential equation that describes the time evolution of quantum systems and is central to quantum mechanics.
- 🚀 For a small time interval, the system's evolution is characterized by an expression involving the Hamiltonian, leading to the concept of the Hamiltonian as the generator of time translations.
- 🧲 In the presence of a magnetic field, the energy of a spin system is given by the dot product of the spin vector and the magnetic field, represented by the Hamiltonian.
- 🎭 The expectation values of observables change over time due to the time evolution of the state vector, which can be calculated using the time derivative of the expectation value.
- 🔄 The time derivative of the average of an operator is related to the average of the commutator with the Hamiltonian, showcasing the Hamiltonian's significance in physics.
- 🤝 Non-interacting systems have Hamiltonians that are the sum of the individual Hamiltonians, and if they are interacting, the energy eigenvalues are not simply additive.
- 🌟 Eigenvectors of the Hamiltonian evolve over time by acquiring a phase factor, which is a complex exponential involving the eigenvalue and the Hamiltonian.
- ⚖️ The conservation law associated with the Hamiltonian implies that the expectation value of the energy (Hamiltonian) does not change with time, reflecting the conservation of energy.
Q & A
How does the state of a quantum system change with time?
-The state of a quantum system changes with time through the application of a linear operator, which is time-dependent. This is based on the postulate that state vectors change linearly with time.
What is the significance of the Hamiltonian in quantum mechanics?
-The Hamiltonian is a hermitian operator that represents the total energy of the system. It is significant because it governs the time evolution of the quantum state and is used to calculate expectation values and probabilities of measurements.
What is the role of the unitary operator U in the time evolution of quantum states?
-The unitary operator U ensures the conservation of probability and the preservation of the inner product structure of the state space. It describes how the state vector changes with time while maintaining the norm of the state vector.
Why is the Hamiltonian considered to be a conserved quantity?
-The Hamiltonian is considered conserved because its eigenvalues, which correspond to the energy levels of the system, do not change over time. This is reflected in the fact that the expectation value of the Hamiltonian remains constant as the system evolves.
How does the expectation value of an observable change with time?
-The expectation value of an observable changes with time according to the time derivative of the observable's average value, which is related to the average of the commutator of the Hamiltonian with the observable.
What is the Schrodinger equation?
-The Schrodinger equation is a differential equation that describes how the quantum state of a physical system changes with time. It is represented as iħ(d/dt)|ψ(t)⟩ = H|ψ(t)⟩, where i is the imaginary unit, ħ is the reduced Planck constant, |ψ(t)⟩ is the state vector, and H is the Hamiltonian operator.
What is the difference between a bra and a ket in quantum mechanics?
-A bra is a type of quantum state that is dual to a ket. While a ket is represented as a column vector, a bra is represented as a row vector. The bra is associated with the complex conjugate transpose of a ket, and together they are used to form inner products in the state space.
How does the energy of a quantum system relate to its Hamiltonian?
-The energy of a quantum system is represented by the eigenvalues of its Hamiltonian. The Hamiltonian operator, when acting on an energy eigenstate, simply returns the eigenstate multiplied by its corresponding energy value.
What is the concept of degeneracy in quantum mechanics?
-Degeneracy in quantum mechanics refers to the situation where there are two or more than two linearly independent state vectors corresponding to the same eigenvalue. This means that there is more than one state with the exact same energy.
How does a spin in a magnetic field evolve over time?
-A spin in a magnetic field precesses around the magnetic field direction. The component of the spin along the magnetic field direction remains constant due to energy conservation, while the components in the plane perpendicular to the magnetic field rotate, resulting in a precessional motion.
What is the principle behind the addition of angular momenta in quantum mechanics?
-The principle behind the addition of angular momenta in quantum mechanics is that the total angular momentum of a system is the vector sum of the individual angular momenta. This is relevant when considering systems with multiple particles, each having its own intrinsic spin and orbital angular momentum.
Outlines
😀 Introduction to Quantum Systems and Time Evolution
The paragraph begins with an introduction to the topic of quantum systems and their evolution over time. It emphasizes the importance of revisiting previous material to ensure a solid understanding. The lecturer discusses the state of a quantum system, described by a ket vector, and the concept of time dependence. The central role of linear operators in the time evolution of quantum states is introduced, with an explanation of the postulate that state vectors change linearly. The paragraph also covers the complex conjugate rule for bra vectors and the assumption of probability conservation, leading to the introduction of unitary operators.
🧐 Probing the Inner Product and Time Invariance
This section delves into the inner product of vectors and its time invariance, which is a consequence of the assumption that the length of every vector remains unchanged. The lecturer explains how the inner product between any pair of vectors remains constant over time. The concept of the total probability and its conservation is also discussed, leading to the introduction of the general statement involving the product of state vectors and the inner product.
📚 Unitary Operators and the Hamiltonian
The paragraph introduces the concept of unitary operators, which are crucial for maintaining the probability conservation in quantum mechanics. It explains that the product of a unitary operator and its conjugate transpose results in the unit operator. The lecturer then explores the idea of allowing time to evolve for a very short amount and the concept of an infinitesimal change. The Hamiltonian is introduced as a hermitian operator representing the total energy of the system and is shown to be related to the observables that can be measured in a laboratory.
🔍 The Hamiltonian and Energy Conservation
The focus of this paragraph is on the Hamiltonian and its role in quantum mechanics. It discusses the Hamiltonian as an operator that corresponds to energy and how it is derived from the condition that the expectation value of the Hamiltonian does not change with time. The conservation of energy is highlighted as a fundamental principle, and the Hamiltonian's role in describing the energy of a system is emphasized.
🤔 The Schrodinger Equation and Eigenvectors
This section introduces the Schrodinger equation, which describes how the state vector of a quantum system changes with time. The lecturer explains the process of solving the Schrodinger equation for eigenvectors of the Hamiltonian and discusses the time dependence of these eigenvectors. The concept of energy eigenstates and their evolution with time is also covered, providing insight into the general solution of the Schrodinger equation.
🌀 Time Evolution of Quantum States
The paragraph discusses the time evolution of quantum states, particularly focusing on eigenvectors of the Hamiltonian. It explains that each eigenvector evolves with its own frequency, leading to a general solution for the time evolution of any quantum state. The lecturer also touches on the Fourier series and the concept of superposition of energy eigenstates, illustrating how the Hamiltonian allows for the expansion of any state of a system in terms of its eigenvectors.
📉 Derivatives and Expectation Values
This section explores the time derivative of expectation values of observables in quantum mechanics. The lecturer derives the equation for the time derivative of the expectation value of an observable and relates it to the commutator of the Hamiltonian with the observable. The importance of the Hamiltonian in determining the rate of change of observables is emphasized, and the concept of conserved quantities is introduced.
🧲 A Spin in a Magnetic Field
The paragraph presents a detailed example of a quantum mechanical problem involving a single spin in a magnetic field. It discusses the Hamiltonian for a spin in a magnetic field and calculates the time dependence of the averages of the three components of the spin. The lecturer shows that the spin component along the magnetic field direction remains constant, while the components in the plane perpendicular to the field undergo precession, illustrating the motion of the spin vector.
🤹 Two Electrons in a Magnetic Field
This section deals with the problem of two electrons providing a magnetic field for each other. The Hamiltonian for this scenario is introduced, and the energy eigenvalues and eigenvectors are discussed. The concept of degenerate energy levels is explained, and the states are categorized into singlet and triplet states. The time evolution of the system is explored, showing how the probabilities of the up-down and down-up states change over time.
🔄 Oscillation and Energy Difference
The final paragraph focuses on the oscillation between up-down and down-up states and how it is related to the difference in energies of the singlet and triplet states. The lecturer demonstrates how to calculate the frequency of this oscillation and emphasizes that the probabilities depend only on the difference in energies, not the overall sum. The general approach to solving quantum mechanical problems is summarized as a ritual that involves expanding in terms of energy eigenvectors, evolving with their respective phases, and then recombining in the original basis.
Mindmap
Keywords
💡Quantum State
💡Linear Operator
💡Unitary Operator
💡Hermitian Operator
💡Hamiltonian
💡Schrödinger Equation
💡Eigenvector and Eigenvalue
💡Expectation Value
💡Commutator
💡Conservation Law
💡Spin in a Magnetic Field
Highlights
The state of a quantum system is described by a ket vector, which evolves over time under the influence of a linear operator.
The time evolution of quantum states is postulated to be linear, a concept rooted in experimental evidence and theoretical consistency.
The total probability of a quantum system is conserved over time, which is ensured by the system's state vectors satisfying the condition that their inner product equals 1.
The time derivative of the inner product of any two state vectors is shown to be time-independent, a fundamental property for quantum state evolution.
The operator governing the time evolution of quantum states, denoted as U, is unitary, ensuring the preservation of the probability norm.
For an infinitesimal time interval, the evolution operator U can be approximated, leading to the introduction of the Hamiltonian H, a Hermitian operator representing the system's energy.
The Hamiltonian is identified as the operator associated with the energy of the system, a concept that is conserved and central to the dynamics of quantum systems.
The Schrödinger equation is derived, which describes how the quantum state of a system changes with time, represented as d/dt |ψ> = -iħH |ψ>.
Eigenvectors of the Hamiltonian evolve over time by acquiring a phase factor, which is a function of the eigenvalue and the time elapsed.
The expectation value of an observable A changes over time according to the equation d/dt <A> = iħ <[H, A]>, where [H, A] is the commutator of the Hamiltonian and the observable.
The Hamiltonian's role in physics is highlighted as it allows for the calculation of how observables evolve over time through their commutators with H.
The expectation value of the Hamiltonian itself does not change with time, reflecting the conservation of energy in quantum systems.
The concept of degeneracy in quantum mechanics is introduced, where multiple states share the same energy eigenvalue.
The problem of a spin in a magnetic field is explored, revealing that the spin vector precesses around the magnetic field direction.
The time evolution of a quantum state can be computed by expanding it in the energy eigenbasis of the Hamiltonian, applying the phase factor to each eigenvector, and recombining them.
An example of two entangled electrons is discussed, illustrating how their spins can oscillate between different states due to their interaction energy differences.
The overall phase of a quantum state is shown to be unimportant in the calculation of probabilities, as it does not affect the observable outcomes.
The program concludes with a demonstration of how to solve quantum mechanical problems by following a standard ritual of expansion, phase application, and recombination.
Transcripts
Browse More Related Video
Lecture 5 | The Theoretical Minimum

Lecture 4 | The Theoretical Minimum

24. Quantum Mechanics VI: Time-dependent Schrödinger Equation

Lecture 9 | The Theoretical Minimum

Lecture 8 | Quantum Entanglements, Part 1 (Stanford)
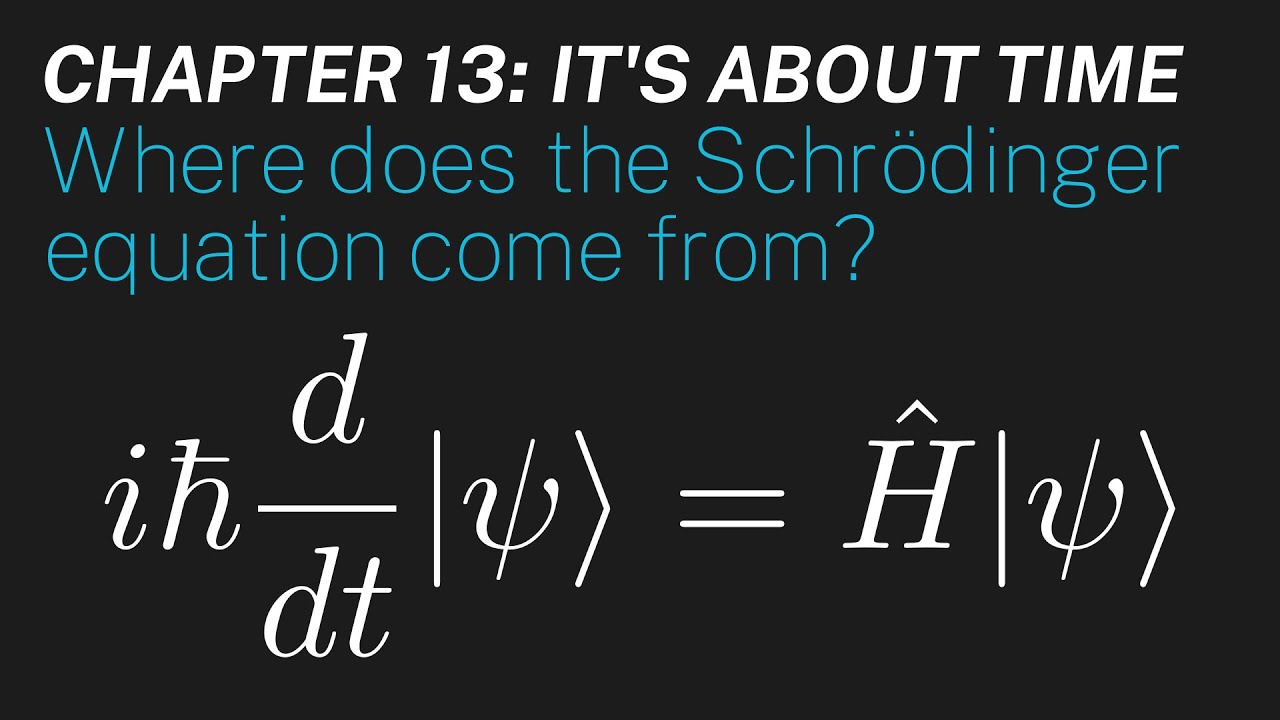
Ch 13: Where does the Schrödinger equation come from? | Maths of Quantum Mechanics
5.0 / 5 (0 votes)
Thanks for rating: