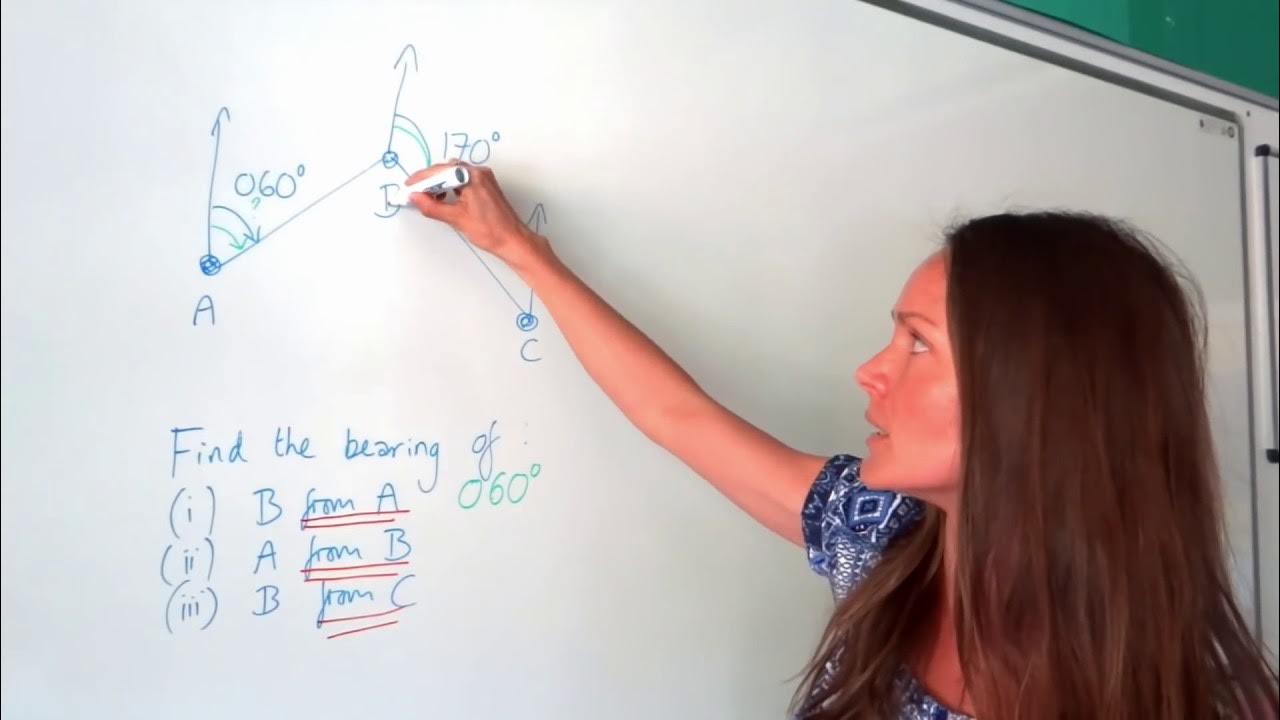
Drawing Bearings Using a Protractor
TLDRThe video script offers a clear guide on how to draw bearings, which are directions measured from a specific point. It emphasizes that bearings are always measured clockwise from a north line. The video demonstrates two methods for drawing bearings, including a 90-degree bearing by aligning a protractor with the north line and a 225-degree bearing using either an extension of the north line to add 45 degrees or by subtracting the desired bearing from 360 degrees to find the complementary angle. The script also mentions that bearings are typically represented with three figures and suggests that viewers will learn to draw scale drawings in a subsequent video, which will help with questions involving both direction and distance.
Takeaways
- 📐 **Protractor Essential**: A protractor is needed to measure angles when drawing bearings.
- 📍 **Fixed Point**: Bearings are always measured from a specific point, which should be marked on the paper with plenty of space around it.
- ↗️ **North Line**: Draw a north line straight up from the chosen point to establish the reference for clockwise measurements.
- 🔄 **Clockwise Measurement**: Bearings are measured clockwise from the north line.
- 🔢 **Three-Figure Bearings**: Bearings are typically represented by three digits.
- 📐 **90-Degree Bearing**: To draw a 90-degree bearing, align the protractor so that the zero degree mark is on the north line and measure 90 degrees around to mark the point.
- 🤔 **Large Bearings**: For bearings greater than what the protractor shows directly, extend the north line and calculate the remaining degrees needed.
- 🔄 **180-Degree Extension**: If the bearing is over 180 degrees, find the 180-degree mark and then measure the additional degrees required to reach the desired bearing.
- 🛤️ **Alternative Method**: For large bearings, measure the angle that is not needed (360 - bearing degrees) to find the desired direction.
- 📏 **Scale Drawings Next**: After bearings, the video will cover scale drawings, which will include both direction and distance.
- ✍️ **Marking Bearings**: Once the bearing line is drawn, it should be labeled with the bearing degree for clarity.
Q & A
What is a bearing and how is it typically described?
-A bearing is a direction of travel or orientation relative to a reference point, typically measured in degrees clockwise from true north. It is used to describe the direction of movement, such as an airplane's flight path or a person's walking direction from a starting point.
What tool is required to measure the angles for bearings?
-A protractor is required to measure the angles for bearings, as it allows for precise angle measurements which are essential in determining the correct bearing.
How do you start drawing a bearing on a piece of paper?
-To start drawing a bearing, first choose a point on the paper that represents the reference point. Then, leave plenty of space around it and draw a north line straight up from that point.
In which direction are bearings measured from the north line?
-Bearings are measured clockwise from the north line. This means you start at the north line and move around the protractor in a clockwise direction to the desired degree.
How do you draw a bearing of 90 degrees?
-To draw a bearing of 90 degrees, align the center of the protractor with the reference point, ensure the zero line of the protractor is on the north line, and then find the 90-degree mark on the protractor to mark point B and draw a line to it.
What is the standard format for writing down a bearing?
-Bearings are typically written with three figures, for example, '090' for a bearing of 90 degrees. This format helps to maintain precision and clarity.
How can you approach drawing a bearing that is greater than what your protractor can directly measure, such as 225 degrees?
-For bearings greater than what the protractor can directly measure, you can extend the north line and measure the remaining degrees needed to reach the total bearing. For a 225-degree bearing, you would measure 45 degrees from the 180-degree line extended from the north line.
What is an alternative method to measure a large bearing like 225 degrees?
-An alternative method is to measure the angle that you don't want, which is 360 degrees minus the desired bearing. For a 225-degree bearing, you would measure 135 degrees clockwise from the north line using the inside scale on the protractor.
Why is it important to understand the context when discussing bearings?
-Understanding the context is important because bearings are always measured from a specific point, such as an airport or a tent, and the context provides the necessary reference for the bearing's starting point.
What is the next step after learning to draw bearings?
-The next step after learning to draw bearings is to learn how to incorporate scale drawings, which will involve not only direction (bearings) but also distances, to answer a broader range of questions.
How can you ensure accuracy when drawing bearings?
-To ensure accuracy, always use a protractor for measuring angles, start from a clearly defined reference point, and make sure to measure clockwise from the north line. Double-check your measurements before marking the final bearing on the paper.
What is the significance of using three figures for bearings?
-Using three figures for bearings provides a standardized and precise way to communicate the direction, which is especially important in navigation where small errors can lead to significant deviations from the intended path.
Outlines
📐 Understanding and Drawing Bearings
This paragraph explains the concept of bearings and how to draw them. Bearings are always measured from a point and are expressed in degrees, clockwise from a north line. To draw a bearing, you need a protractor for measuring angles. The video demonstrates how to draw a bearing of 90 degrees by aligning the protractor's center with the point, setting the zero line on the north line, and marking the 90-degree position. For larger bearings, such as 225 degrees, which cannot be directly measured with a standard protractor, the video shows two methods: extending the north line and measuring the remaining degrees from there, or calculating the difference from a full circle (360 degrees minus the bearing angle) and measuring that angle instead. The importance of using the correct scale on the protractor is emphasized, and the video concludes with a teaser for the next topic: drawing bearings with a scale, which will include both direction and distance.
🧮 Alternative Method for Drawing Bearings
The second paragraph delves into an alternative method for drawing bearings that are not directly measurable with a standard protractor, such as a bearing of 225 degrees. The video suggests calculating the difference from a full circle (360 degrees) to find the angle that is not wanted and then measuring from the north line. For instance, if the bearing is 225 degrees, one would measure 135 degrees (360 - 225) using the inner scale of the protractor. This method provides an alternative way of thinking about the problem and offers a different approach to finding the correct bearing. The video assures viewers that both methods will yield the same result, and they can choose the one they find more intuitive or easier to understand.
Mindmap
Keywords
💡Bearings
💡Protractor
💡North Line
💡Clockwise Measurement
💡Degrees
💡Point of Origin
💡Context
💡Three-Figure Bearings
💡Bearing Calculation
💡Scale Drawing
💡Direction and Distance
Highlights
A video tutorial is provided to explain how to draw bearings.
Bearings are always measured from a point and are contextual, such as an airplane's direction from an airport.
A protractor is required for measuring angles when drawing bearings.
Bearings are measured clockwise from a north line drawn on the paper.
The north line is a straight vertical line on the paper, representing the starting point for measuring bearings.
A bearing of 90 degrees is demonstrated by aligning the protractor's center with the point and the zero line on the north line.
Bearings are typically marked with three figures, for example, 090 degrees for a bearing of 90 degrees.
For larger bearings, such as 225 degrees, the protractor may not directly measure the angle, requiring alternative methods.
One method for larger bearings involves extending the north line and measuring the additional degrees needed to reach the desired bearing.
An alternative approach for bearings over 180 degrees is to measure the angle that is not needed by subtracting the desired bearing from 360 degrees.
The bearing of 225 degrees can be found by measuring 135 degrees counterclockwise from the extended north line.
Different methods for drawing bearings are presented to accommodate varying levels of understanding and preference.
The importance of measuring bearings clockwise from the north line is emphasized, regardless of the method used.
The tutorial suggests that the easiest method of measuring bearings should be used based on personal preference and understanding.
The next step in the tutorial is to address scale drawings, incorporating both direction and distance.
Scale drawings will help answer more complex questions involving bearings and distances.
The video tutorial aims to simplify the process of drawing bearings and understanding their context and measurement.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: