Bearings - Corbettmaths
TLDRThis educational video script delves into the concept of bearings, which are directions of travel measured clockwise from north. It explains how to calculate bearings in degrees, emphasizing the use of a protractor and the importance of a north line for accurate measurements. The script covers various scenarios, including finding the bearing from one location to another and determining locations given a bearing and distance. It also addresses how to represent bearings with three-figure numbers, using leading zeros when necessary. Practical examples are provided, such as calculating the bearing between Antrim and Belfast as 104 degrees, and the distance between two points on a map given a scale. The video concludes with a demonstration of marking a location on a map using a bearing and distance, specifically finding Boston's position relative to Redville. The script is an informative guide for understanding and applying bearings in navigation and geography.
Takeaways
- 🧭 A bearing is a direction of travel, measured clockwise from north.
- 📏 Bearings are given as three-figure numbers, with a leading zero if less than 100 degrees.
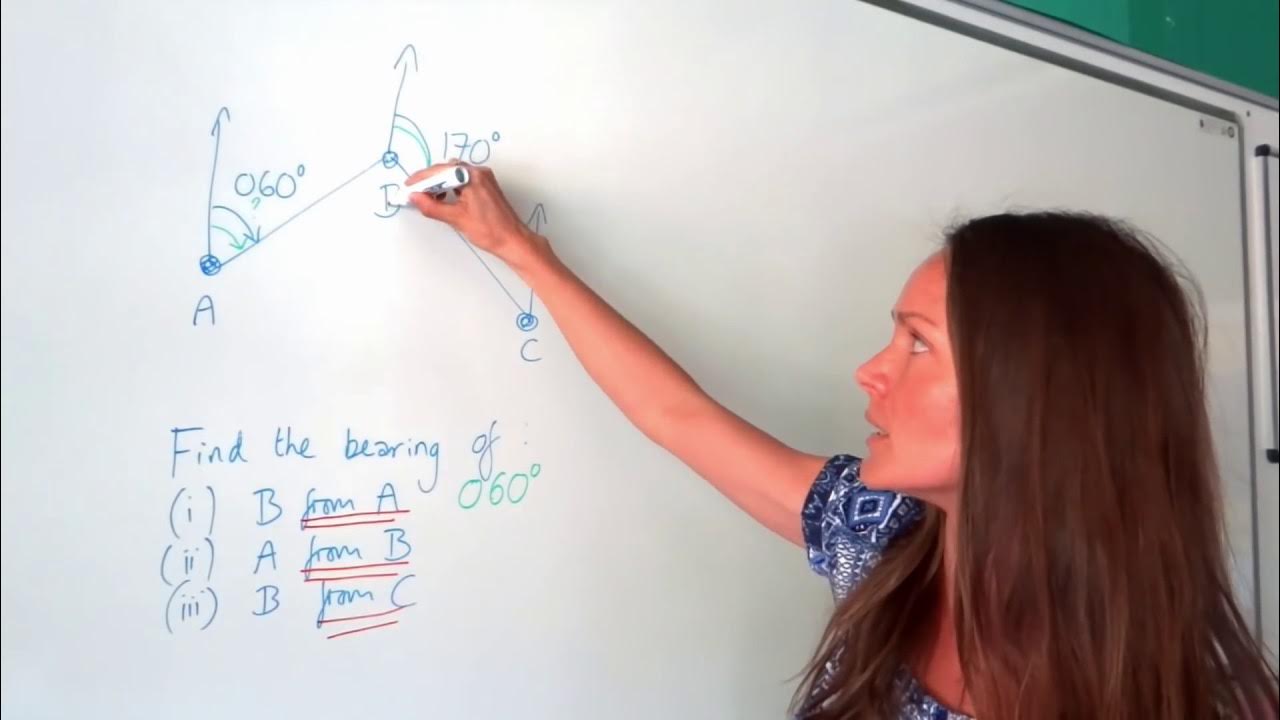
- 👉 To find the bearing from one point to another, draw a line between the points and measure the angle from the north line to this line.
- 📐 Use a protractor to measure the angle, ensuring the zero is at the top and aligned with the north line.
- 🔄 If the angle is greater than 180 degrees (reflex angle), measure the angle with the protractor and add it to 180, or subtract the acute angle from 360.
- 🌐 For large angles, a 360-degree protractor can be useful for directly reading the bearing.
- 📏 When given a scale on a map, use it to calculate the actual distance between two points by multiplying the scale factor by the measured distance on the map.
- 🏠 To find the distance between two points on a map with a scale, measure the distance on the map in centimeters and multiply by the scale factor to get the real-world distance.
- 📍 To mark a location on a map given a bearing and distance, draw the direction from the starting point using the bearing and then measure the distance to find the exact location.
- 🔢 Always ensure to present bearings as three-figure bearings, even if the direction is north, east, south, or west, using 000, 090, 180, and 270 respectively.
- 🤝 The process of finding bearings and distances involves both mathematical calculation and geographical understanding of direction and scale.
Q & A
What is a bearing and how is it measured?
-A bearing is the direction of travel, measured clockwise from north. It is typically given as a three-figure number, where if the bearing is less than 100, a zero is placed in front.
If you are traveling in a direction that is 130 degrees clockwise from north, what is your bearing?
-If you are traveling in a direction that is 130 degrees clockwise from north, your bearing is 130 degrees.
What bearing would you have if you were traveling directly north?
-If you were traveling directly north, your bearing would be 000 degrees.
How do you calculate the bearing of one location from another on a map?
-To calculate the bearing of one location from another, you first join the two locations with a straight line. Then, you draw a north line at the starting location and measure the angle clockwise from the north line to the line connecting the two locations.
What is the bearing of Belfast from Antrim according to the script?
-The bearing of Belfast from Antrim is 104 degrees, as measured by drawing a north line at Antrim and measuring the angle clockwise to the line connecting Antrim and Belfast.
How do you measure a reflex angle, which is an angle greater than 180 degrees, to find the bearing?
-To measure a reflex angle, you can either measure the angle clockwise from north to the line and then add any additional angle to reach 360 degrees, or you can measure the acute angle directly opposite the reflex angle and subtract it from 360 degrees.
What is the bearing of Castletown from Milton in the script?
-The bearing of Castletown from Milton is 044 degrees, which is a three-figure bearing calculated by measuring the angle from the north line at Milton to the line connecting Milton and Castletown.
How do you find the actual distance between two points on a map when given a scale?
-To find the actual distance between two points on a map with a given scale, you measure the distance on the map in the units provided by the scale (e.g., centimeters), and then multiply that measurement by the conversion factor given by the scale (e.g., how many meters or kilometers each unit on the map represents).
What is the actual distance between point C and point D on the map, given a scale where one centimeter represents 200 meters and the measured distance is six centimeters?
-The actual distance between point C and point D is 1200 meters, calculated by multiplying the measured distance of six centimeters by the scale factor of 200 meters per centimeter.
If the bearing from Redville to Boston is 110 degrees and the actual distance is 30 kilometers, how would you mark Boston's location on a map with a scale of one centimeter representing five kilometers?
-You would draw a line from Redville in the direction of 110 degrees and mark a point six centimeters away from Redville on that line, since 30 kilometers is equivalent to six centimeters on the map (30 km / 5 km per cm = 6 cm).
What bearing and distance would you calculate for the house relative to the shop on the island, given a scale of one centimeter representing 250 meters?
-The bearing of the house from the shop is 117 degrees, measured clockwise from the north line at the shop to the line connecting the shop and the house. The distance between the house and the shop is 2000 meters, calculated by multiplying the measured distance of eight centimeters by the scale factor of 250 meters per centimeter.
Outlines
🧭 Introduction to Bearings
This paragraph introduces the concept of bearings, which are directions of travel measured clockwise from north. It explains how to calculate bearings using angles and provides examples of bearings for different cardinal directions. The paragraph also discusses how to measure the bearing from one location to another using a diagram, a north line, and a protractor. It concludes with an example of finding the bearing of Belfast from Antrim.
📐 Measuring Bearings and Distances
This section delves into the methods for measuring bearings, specifically when dealing with reflex angles, which are angles greater than 180 degrees. It outlines two approaches: measuring the angle with a protractor and adding it to 180 degrees or subtracting an acute angle from 360 degrees. The paragraph also covers how to use a scale to find the actual distance between two points on a diagram, as demonstrated with points C and D. Additionally, it explains how to find the bearing from one point to another using the same techniques, as shown with the bearing from D to C.
🌎 Locating Points on a Map
This part of the script focuses on how to mark the location of a place on a map when given a bearing and distance. Using Redville as a starting point, the video shows how to calculate the position of Boston based on a bearing of 110 degrees and a distance of 30 kilometers. It demonstrates the process of drawing the line of bearing from Redville, measuring the distance on the map using a given scale, and marking the location of Boston accordingly.
🏠 Finding Bearings and Distances on a Local Scale
The final paragraph deals with finding both the bearing and the distance between two local points, specifically a shop and a house on an island. It explains how to join the two points and draw a north line from the starting point to measure the bearing using a protractor. The bearing from the shop to the house is determined to be 117 degrees. To find the distance between the two points, the script describes measuring the distance on the diagram, applying the given scale—where one centimeter represents 250 meters—and calculating the actual distance, which in this case is 2000 meters.
Mindmap
Keywords
💡Bearing
💡North Line
💡Three-Figure Bearing
💡Protractor
💡Acute and Reflex Angles
💡Scale
💡Actual Distance
💡Map Location
💡Direction of Travel
💡Diagram
💡Distance Measurement
Highlights
A bearing is defined as the direction of travel, measured clockwise from north.
Bearings are given in three figures, with a leading zero for angles less than 100 degrees.
If traveling north, the bearing is 000 degrees; east is 090 degrees; south is 180 degrees; and west is 270 degrees.
To find the bearing between two points, join them and measure the angle clockwise from north.
When calculating bearings, use a protractor to measure the angle and ensure accuracy.
For bearings greater than 180 degrees, measure the angle as a reflex angle or subtract from 360 degrees.
A 360-degree protractor can simplify the measurement of large angles by directly reading off the bearing.
When given a scale on a map, use it to convert distances on the diagram to real-world measurements.
To find the actual distance between two points on a scaled diagram, multiply the diagram distance by the scale factor.
When marking a location on a map given a bearing and distance, use a protractor to align with the bearing and a ruler for the distance.
For finding the bearing of one location from another, ensure you start from the correct point and measure the angle to the line connecting the two locations.
When the bearing angle is less than 100 degrees, a leading zero is added to maintain the three-figure format.
In the context of a diagram, the north line is crucial for establishing the starting point for bearing measurements.
To measure the bearing of a location, draw a line from the starting point to the location and measure the angle clockwise from north.
When calculating the distance between two points on a map with a given scale, measure the distance on the map and multiply by the scale to get the real-world distance.
For bearings over 180 degrees, one method is to measure the smaller angle and subtract it from 360 degrees to find the bearing.
A 360-degree protractor can be a useful tool for directly measuring and reading bearings without additional calculations.
When given a bearing and distance, you can plot a point on a map by using the bearing to find the direction and the distance to find the scale.
In summary, bearings are measured clockwise from north and are always expressed in three figures, with leading zeros where necessary.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: