Bearings In Maths
TLDRIn this engaging Minty Maths video, viewers are introduced to the concept of bearings, which are measurements of direction from one point to another, expressed as angles between 0 and 360 degrees. The video explains that bearings are crucial for navigation, such as guiding a ship to its destination or finding one's way in the woods with just a compass and a map. The script outlines the process of calculating bearings by starting from the north and turning clockwise, often using a protractor for precise measurements. It also addresses scenarios where a protractor is not available, illustrating how to apply geometry rules to find bearings when given certain angles, such as alternate angles in parallel lines. The video concludes with a method for determining the exact location of an object using two known bearings, by drawing out the angles and finding the point of intersection. This comprehensive guide is designed to help viewers understand and apply bearings in various navigational contexts.
Takeaways
- 🧭 A bearing is a measure of direction from one point to another, expressed as an angle between 0 and 360 degrees.
- 📐 Bearings are measured starting from north and turning clockwise.
- 🚢 Bearings are crucial for navigation, helping ships and other vehicles determine the direction to their destination.
- 🏞️ In situations like being lost in the woods, a compass, map, and protractor can be used with bearings to find one's way.
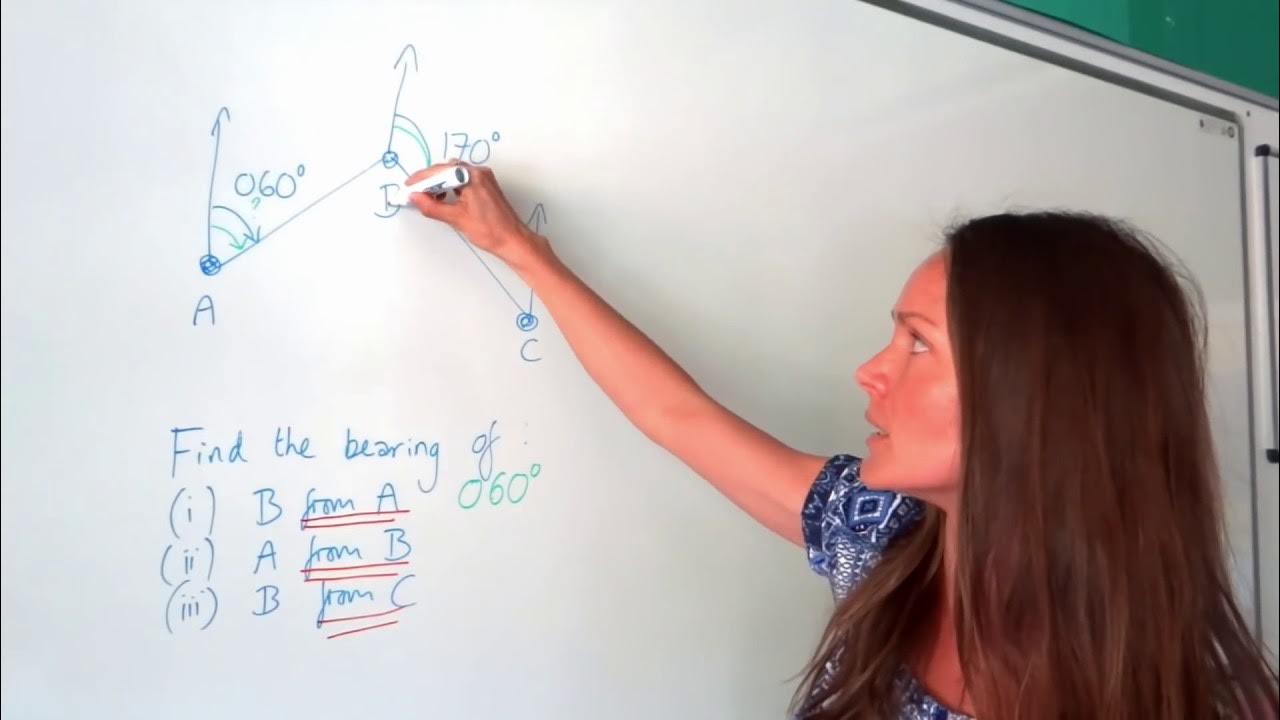
- 📌 The term 'from' in a question indicates the starting point for calculating the bearing.
- 📏 To find the bearing, draw a line from the starting point towards north and then to the destination point, measuring the angle clockwise from north.
- 📐 A protractor is often used to measure the angle for bearing calculations.
- 🔢 Bearings are typically written with three figures, even if the angle is usually expressed with two.
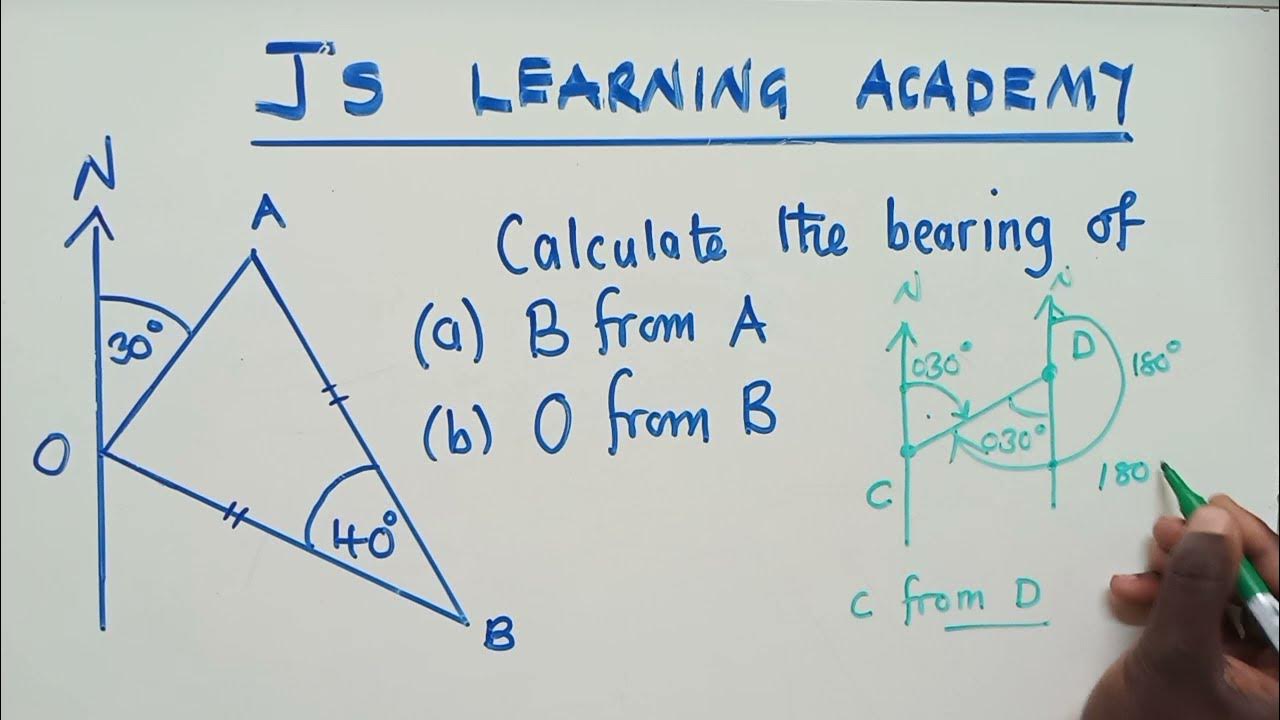
- 🔁 If given the bearing from a boat to an island, you can find the reverse bearing by subtracting 180 degrees from the given angle due to parallel line geometry rules.
- 🔍 To find the exact location of an object with two bearings, draw out each bearing from the respective points and find where the lines intersect.
- 👤 When drawing bearings from multiple points to a location, extend the lines far enough to ensure they cross at the correct point.
- 🎓 Understanding geometry rules, such as alternate angles being equal in parallel lines, can help in calculating bearings without a protractor.
Q & A
What is a bearing and how is it measured?
-A bearing is a measure of direction from one point to another, expressed as an angle between 0 and 360 degrees. It is measured starting from the north and turning clockwise.
Why are bearings important in navigation?
-Bearings are crucial for navigation as they help determine the direction in which a ship or any other vehicle should travel to reach its destination.
What is the significance of the word 'from' in a bearings question?
-The word 'from' in a bearings question indicates the starting point for measuring the bearing.
How do you use a protractor to measure a bearing?
-To measure a bearing with a protractor, place the zero-degree mark on the line facing north and align the protractor so that the line between the two points of interest intersects the scale on the protractor, indicating the bearing angle.
What should be the format for writing down a bearing?
-Bearings are always written with three figures, even if the angle is usually only two figures.
How can you find the reverse bearing from the given boat to the island?
-If you know the bearing of the boat from the island, you can find the reverse bearing by subtracting 180 degrees from the given angle because the lines are parallel and alternate angles are equal.
What is the role of geometry rules in bearings calculations?
-Geometry rules are applied when you need to find bearings without a protractor by using the properties of parallel lines and the relationships between angles.
How do you find the exact location of an object given two bearings?
-To find the exact location, draw out the bearings from each given point and extend each line until they cross. The point of intersection is the location of the object.
What is the first step in drawing a bearing from a starting point?
-The first step is to draw a line going north from the starting point since all bearings are measured from north.
Why do you extend the line quite far when drawing a bearing?
-Extending the line far ensures accuracy in finding the point of intersection, especially when dealing with bearings from multiple points.
How can you practice finding bearings?
-You can practice by attempting the provided practice questions in the script and pausing the video to work through the calculations on your own.
What additional resources are available for learning about angles in parallel lines?
-For a reminder of angles in parallel lines, you can watch the video linked above in the script, which is part of the Minty Maths series.
Outlines
🧭 Introduction to Bearings
This paragraph introduces the concept of bearings, which are measurements of direction from one point to another, expressed as angles between 0 and 360 degrees. It emphasizes that bearings are measured starting from the north and turning clockwise. The importance of bearings in navigation is highlighted, particularly for ships finding their way to a destination. The paragraph also suggests that bearings can be crucial for personal navigation, such as when one is lost in the woods with only a compass, a map, and a protractor.
Mindmap
Keywords
💡Bearing
💡North
💡Clockwise
💡Navigation
💡Compass
💡Protractor
💡Angles
💡Geometry Rules
💡Parallel Lines
💡Practice Question
💡Minty Maths
💡Script
Highlights
Bearings are a measure of direction from one point to another, written using angles between 0 and 360 degrees.
Bearings are measured starting from north and turning clockwise.
Bearings are often used for navigation, such as for ships determining the direction to travel to reach their destination.
In a bearing calculation, the word 'from' indicates the starting point.
A line is drawn going north from the starting point before drawing a line between the two points of interest.
A protractor is commonly used to measure the angle for many bearing questions.
Bearings are written with three figures, even if the angle is typically two figures.
If the bearing of one point from another is known, geometry rules can be applied to find the reverse bearing.
Alternate angles within parallel lines are equal, which can be used to calculate the reverse bearing.
To find the exact location of an object given two bearings, draw out the bearings from each point until the lines cross.
When given bearings from two different people to a point, such as a cafe, the location of the cafe is where the two lines intersect.
For practice, viewers are encouraged to pause the video and attempt a bearing calculation question.
The video provides a link to a reminder of angles in parallel lines for those needing a refresher.
The channel offers weekly math videos, inviting viewers to subscribe for more content.
The video concludes with a call to action, encouraging viewers to try out a practice question related to bearings.
Bearings can be a crucial tool for navigation and are applicable in various real-world scenarios, such as getting out of being lost in the woods.
The video explains how to use a protractor to measure the angle for calculating a bearing, emphasizing the importance of starting from north.
In cases where a protractor is not available, the video demonstrates alternative methods using geometry rules to find bearings.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: