GCSE Maths - What are Bearings? #118
TLDRThis video tutorial delves into the concept of bearings, crucial for navigation. It begins by illustrating how to find the bearing from point A to point B, emphasizing the need to measure angles starting from the north and moving clockwise. The importance of expressing bearings in three digits is highlighted, with an example of converting a 65-degree angle to 065 degrees. The video further explains how to handle bearings greater than 180 degrees, such as a 310-degree bearing, by measuring smaller angles and using subtraction to find the correct bearing. Practical tips are provided for using protractors and dealing with full-circle calculations. The tutorial concludes with a realistic exam-style problem involving two individuals, A and B, trying to locate a pond using bearings from their respective positions. By drawing the bearings on a diagram and finding the intersection, the video demonstrates how to accurately pinpoint the pond's location, marking it with a cross labeled 'P'. The video is an informative guide for those looking to understand and apply bearings in navigation.
Takeaways
- 🧭 Bearings are used in navigation to determine direction from one point to another.
- 📐 To find a bearing, you start measuring angles from the north.
- 🔄 Always measure the angle clockwise from north to find the correct bearing.
- 🔢 Bearings are typically written as three-digit numbers to maintain precision.
- 🚫 Protractors usually measure up to 180 degrees, so for larger angles, you might need to calculate the difference from 360 degrees.
- 📍 When given bearings from two different points, you can find the location of an object where the bearing lines intersect.
- 🔗 Understanding the three key rules of bearings is crucial for accurate navigation.
- 🤝 Practice with different scenarios, including those with extra information or more complex tasks, to improve navigation skills.
- 📉 In exams, bearing questions might include additional complexities, so it's important to be comfortable with the basic principles.
- ✅ Use a protractor to measure the angle and draw the bearing line from the starting point.
- ⚙️ For real-world applications, bearings can be used to locate objects, such as a pond in the given example.
- 🎓 The video provides a step-by-step guide on how to use bearings, which is beneficial for educational purposes.
Q & A
What is the primary purpose of using bearings in navigation?
-Bearings are used in navigation to determine the direction one must travel to reach a specific point from a known starting point.
What are the three important rules to remember when working with bearings?
-The three rules are: 1) Always measure the angle starting from north, 2) Always measure the angle clockwise from north, and 3) Always write bearings using three digits.
How do you express a bearing of 65 degrees in the three-digit format?
-A bearing of 65 degrees is expressed as 065 degrees in the three-digit format.
What is the bearing of point P from point Q if the angle measured clockwise from north is 310 degrees?
-The bearing of point P from point Q is 310 degrees.
Why might one need to measure a smaller angle when dealing with a protractor that only goes up to 180 degrees?
-One might need to measure a smaller angle and then use mathematical operations to find the bearing because a protractor that only goes up to 180 degrees cannot measure angles greater than 180 degrees directly.
How can you find the bearing of 310 degrees if your protractor only measures up to 180 degrees?
-You can measure the smaller angle, which is 50 degrees in this case, and then use the calculation 360 - 50 to find the bearing of 310 degrees.
What is the practical implication of measuring a bearing in a real-world exam scenario?
-In real-world exam scenarios, bearing questions often involve more complex tasks, such as interpreting additional information or performing calculations beyond simply finding a bearing.
How do you determine the position of a pond if you know the bearing from two different people?
-You determine the position of the pond by drawing the bearings from both people on a diagram. The pond's position is where the two bearing lines intersect.
What is the bearing of the pond from person A if it is given as 56 degrees?
-The bearing of the pond from person A is 56 degrees, which means you would measure a 56-degree angle clockwise from north to find the pond's location.
What is the bearing of the pond from person B if it is given as 260 degrees?
-The bearing of the pond from person B is 260 degrees, which means you would measure a 260-degree angle clockwise from north to find the pond's location.
How do you mark the position of the pond on a diagram when given bearings from two different points?
-You mark the position of the pond on a diagram by drawing the bearings from both points and finding the point where the two bearing lines cross. You then label this point with a cross and the label 'P'.
Outlines
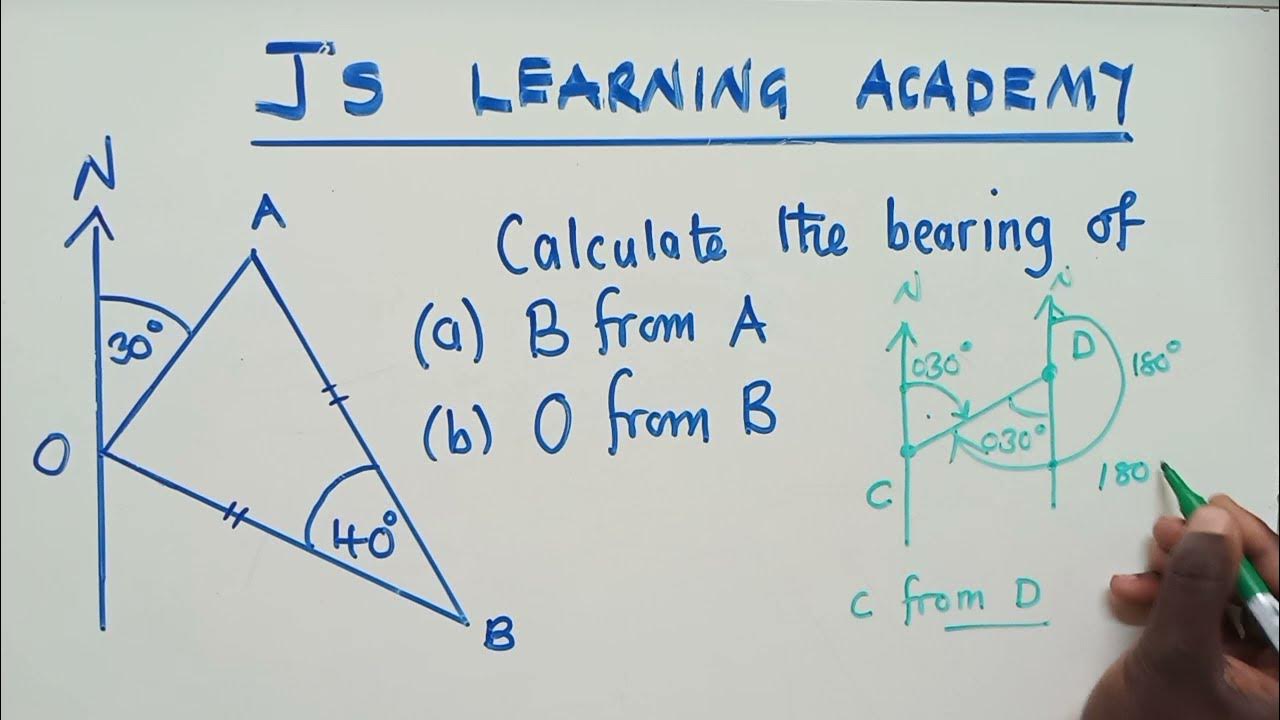
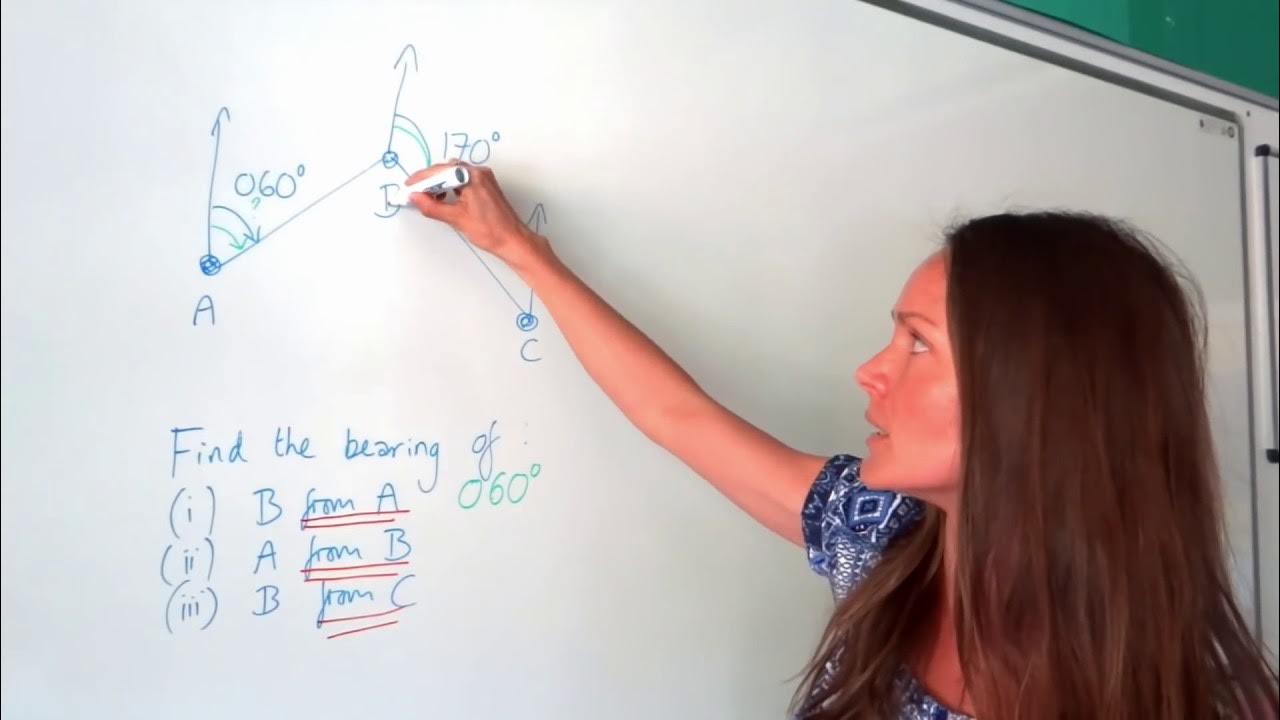
🧭 Understanding Bearings in Navigation
This paragraph introduces the concept of bearings, which are crucial for navigation. It explains that bearings help determine the direction one must travel from a starting point (Point A) to reach a destination (Point B). The content emphasizes three key rules for working with bearings: 1) angles are measured starting from the north, 2) angles are measured clockwise from north, and 3) bearings are written as three-digit numbers to ensure precision. The paragraph also demonstrates how to calculate bearings with examples, including how to deal with angles greater than 180 degrees using a protractor and the concept of a full circle being 360 degrees. Finally, it touches on the complexity of real exam questions, which may involve additional information and more challenging tasks beyond simply finding a bearing.
📍 Marking the Position of a Pond Using Bearings
The second paragraph demonstrates how to apply the concept of bearings to a practical problem. It outlines a scenario where two people, Person A and Person B, are trying to locate a pond. The bearings from both persons to the pond are given (56 degrees from A and 260 degrees from B), and the task is to mark the pond's position with a cross labeled 'P'. The solution involves drawing north arrows, measuring the bearings using a protractor, and plotting them on a diagram. The intersection of the two bearing lines indicates the pond's location. The paragraph also addresses the practicality of using a protractor that measures up to 180 degrees and the method of calculating larger angles by subtracting from 360 degrees. The video concludes with an invitation for viewers to like and subscribe if they found the content useful.
Mindmap
Keywords
💡Bearing
💡Navigation
💡North
💡Clockwise
💡Protractor
💡Three-Digit Bearing
💡Person A and Person B
💡Angle Measurement
💡Complete Circle
💡Examination Style Question
💡Cross
Highlights
The video explains how to use bearings in navigation, specifically finding the direction from one point to another.
Bearing is the direction you need to travel from a starting point to reach a destination.
Three important rules for working with bearings: always measure from north, measure clockwise, and use three digits.
To express a bearing, you must write it with three digits, even if it means leading with zeros.
Practical tip: Most protractors measure up to 180 degrees, so you may need to calculate bearings over 180 degrees.
If a protractor can't measure the full angle, you can measure a smaller angle and subtract it from 360 to find the bearing.
Exam-style questions often include extra information and require more complex problem-solving than just finding a bearing.
In a realistic exam question, you might be given multiple bearings from different points and asked to find the intersection.
To solve such problems, you draw bearings onto the diagram and find the point where they cross to locate the position.
The video demonstrates marking the position of a pond using bearings from two different people's perspectives.
The pond's position is found by drawing bearings from both people's locations and identifying their intersection point.
The video provides a step-by-step guide to drawing bearings and solving for the pond's location.
A north arrow is used to establish the starting direction for measuring bearings.
Angles are measured clockwise from the north arrow to determine the bearing.
The video concludes with an encouragement to like and subscribe for more helpful content.
The video is educational, providing clear instructions on how to use bearings for navigation.
It emphasizes the importance of understanding the rules of bearing measurements for accurate navigation.
The video includes a practical example to illustrate the application of bearings in real-world scenarios.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: