Interpreting Graphs in Chemistry

Melissa Maribel
10 Aug 202005:21
EducationalLearning
32 Likes 10 Comments

TLDRThe video script provides a comprehensive guide on interpreting and graphing data in chemistry labs. It explains the fundamentals of a graph, including the axes, where the x-axis represents the independent variable and the y-axis represents the dependent variable. The importance of labeling axes with units and having a clear title is emphasized. The concept of a 'best fit line' or 'trendline' is introduced, which is a line that approximates a set of data points. The script delves into the equation of a line, 'y = mx + b', where 'm' is the slope and 'b' is the y-intercept, and how understanding this equation can help in determining unknown values. The slope is particularly useful for calculating unknowns and is found using the formula derived from two points. The video also covers how to represent chemistry formulas as line equations and uses an example to illustrate how to find the heat of vaporization from a given data set. It concludes by highlighting the significance of graphing in various chemistry questions and encourages viewers to explore more through provided resources.

Takeaways
  • 📈 **Understanding Graphs**: In chemistry labs, it's crucial to interpret and graph data from experiments to find missing information and determine unknowns.
  • 📊 **Axes and Variables**: The x-axis (horizontal) is the independent variable you control, while the y-axis (vertical) is the dependent variable that changes based on the independent variable.
  • 🔍 **Labeling Axes**: Axes should always be labeled with units of measurement, and there should be a title indicating y versus x.
  • 🧵 **Best Fit Line**: Data points often don't form a perfect line, so a best fit line (or trendline) is used to approximate the data set, which may pass through, none, or all points.
  • 💡 **Graphing Software**: Most graphing software can automatically generate the best fit line for you.
  • 📐 **Slope and Y-Intercept**: The equation of a line is y = mx + b, where 'm' is the slope (rate of change) and 'b' is the y-intercept (point on y-axis).
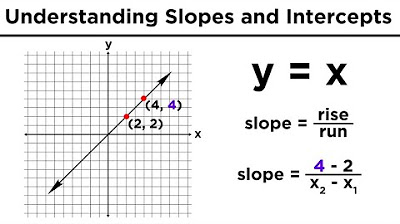
  • 🔢 **Determining Slope**: To find the slope from two points (x1, y1) and (x2, y2), use the formula that involves subtraction and division of the differences in y and x values.
  • 🔬 **Chemistry Formulas**: Some chemistry formulas can represent the equation of a line, which is helpful for understanding the relationship between variables.
  • 🌡️ **Heat of Vaporization Example**: To find the heat of vaporization, you may need to manipulate given data (like taking the natural logarithm of pressure and inverse of temperature), graph it, and use the trendline equation.
  • ✅ **Graph Components**: Ensure your graph has a title, labeled axes with units, a shown best fit line, and the equation of the trendline for lab reports.
  • 📚 **Practice and Application**: Practice different types of graphing questions in chemistry to become proficient in interpreting and using graphs to solve problems.
Q & A

  • What are the two axes of a graph and what are they typically called?

    -The two axes of a graph are the x-axis, which is horizontal, and the y-axis, which is vertical. The x-axis is known as the independent variable, and the y-axis is known as the dependent variable.

  • Why is the x-axis considered the independent variable in an experiment?

    -The x-axis is considered the independent variable because it represents the variable that can be controlled in an experiment. Changes to the x-axis do not depend on other variables.

  • How is the y-axis related to the x-axis in the context of an experiment?

    -The y-axis is known as the dependent variable because its changes are dependent on the independent variable (x-axis). For instance, if time is the independent variable and temperature is the dependent variable, the temperature changes as a result of varying the time.

  • What is the purpose of labeling axes and including units on a graph?

    -Labeling axes and including units is crucial for understanding the graph and the measurements it represents. It provides clarity on what each axis represents and the scale of the measurements.

  • What is a best fit line and why is it used on graphs?

    -A best fit line, also known as a trendline, is a straight line that best approximates a set of data points. It is used because data points often do not form a perfect line, and the best fit line helps to visualize the relationship between variables.

  • How is the equation of a line represented and what does each part signify?

    -The equation of a line is represented as y = mx + b, where 'm' is the slope and 'b' is the y-intercept. The slope (m) signifies the rate of change of y with respect to x, and the y-intercept (b) is the point where the line crosses the y-axis.

  • What is the significance of the slope in the context of a graph?

    -The slope is significant as it represents the rate of change between the dependent and independent variables. It can be used to determine unknown values and understand the relationship between variables.

  • How can you find the slope from two points on a graph?

    -To find the slope from two points, label the points as (x1, y1) and (x2, y2), then use the formula: slope = (y2 - y1) / (x2 - x1). This calculation involves subtracting the y-coordinates and x-coordinates of the two points and then dividing the difference in y by the difference in x.

  • Why is it important to include a title, axis labels with units, and the trendline equation on a graph?

    -Including these elements is important for providing context and clarity to the graph. A title describes the relationship between the variables, axis labels with units indicate the scale and type of measurements, and the trendline equation allows for further analysis and understanding of the data.

  • How can graphing and determining the equation of a trendline help in finding the heat of vaporization?

    -Graphing and determining the trendline equation allows you to visualize the relationship between variables like vapor pressure (ln P) and temperature (1/T). By understanding the slope of the trendline and its units, you can apply the relevant chemistry formulas to calculate the heat of vaporization.

  • What are the typical units for the heat of vaporization and how do you ensure your answer is in these units?

    -The typical units for the heat of vaporization are kilojoules. To ensure your answer is in these units, you can multiply by the appropriate conversion factor (for example, 1000) to convert from joules to kilojoules.

  • What should be done if you are asked to find the slope by hand in chemistry, and what is typically provided instead?

    -Typically, in chemistry, you won't be asked to calculate the slope by hand. Instead, graphing software or a calculator will provide the coefficient in front of the x in the trendline equation, which represents the slope.

Outlines
00:00
📈 Understanding Graphs in Chemistry Labs

This paragraph introduces the importance of interpreting and graphing data in chemistry labs, where students are often tasked with determining unknown variables. It explains the anatomy of a graph, including the roles of the x-axis (independent variable) and y-axis (dependent variable), and the concept of a best fit line, which is a straight line that approximates a set of data points. The paragraph also covers how to interpret the equation of a line (y = mx + b), where 'm' is the slope and 'b' is the y-intercept. It emphasizes the utility of the slope in determining unknown values and provides a formula for calculating the slope from two points (x1, y1) and (x2, y2). The summary concludes with the reminder to include a title, labeled axes with units, the best fit line, and its equation in lab reports. Additionally, it touches on how chemistry formulas can represent the equation of a line and gives an example involving vapor pressure and temperature to illustrate how to find the heat of vaporization using the slope of the trendline.

05:01
🔍 Further Exploration of Graphing in Chemistry

The second paragraph serves as a transition, encouraging viewers to explore additional types of graphing questions commonly found in chemistry. It prompts the audience to click on a link provided in the description to discover more about these questions. The paragraph also acts as a teaser for the next video in the playlist, which presumably will cover more advanced or varied graphing scenarios in chemistry, thus inviting the viewers to continue their learning journey.

Mindmap
Keywords
💡Graph
A graph is a visual representation of data, consisting of two axes, the x-axis (horizontal) and the y-axis (vertical). In the context of the video, graphs are essential for interpreting experimental data in chemistry labs. They are used to find missing information and determine unknown variables by plotting the relationship between an independent variable (x-axis) and a dependent variable (y-axis).
💡Independent Variable
The independent variable is the factor that can be manipulated or adjusted in an experiment. It is represented on the x-axis of a graph. In the video, the concept is exemplified by time in the context of boiling a substance, where the duration of boiling (time) can be controlled, thus making it the independent variable.
💡Dependent Variable
The dependent variable is the outcome or result that changes in response to the independent variable. It is represented on the y-axis of a graph. In the provided script, temperature is used as an example of a dependent variable, as it changes based on the time a substance is boiled.
💡Best Fit Line
The best fit line, also known as the trendline, is a straight line that closely approximates a set of data points on a graph. It may pass through some, none, or all of the data points. This line is crucial in chemistry for making predictions and determining unknowns, as it represents the overall trend of the data. The video emphasizes that most graphing software can automatically generate this line.
💡Slope
The slope of a line, denoted as 'm' in the equation y = mx + b, represents the rate of change of the dependent variable with respect to the independent variable. It is a fundamental concept in understanding how changes in one variable affect another. In the script, the slope is illustrated by the change in mass over the change in volume, which is directly related to the concept of density.
💡Y-Intercept
The y-intercept, denoted as 'b' in the equation y = mx + b, is the point where the line crosses the y-axis. It represents the value of the dependent variable when the independent variable is zero. In the context of the video, the y-intercept is a key component in the linear equation of a graph and helps in determining the starting point of the graphed line.
💡Linear Equation
A linear equation in the context of the video refers to the mathematical representation of a straight line in the form of y = mx + b, where 'm' is the slope and 'b' is the y-intercept. Understanding the linear equation is vital for interpreting the relationship between variables on a graph and for making calculations based on the graphed data.
💡Density
Density is a physical property that is calculated as mass divided by volume. In the script, it is used as an example to illustrate how the slope of a line on a graph can represent a physical property. The slope in a graph showing volume on the x-axis and mass on the y-axis would represent density, making it a key concept in data interpretation.
💡Graphing Software
Graphing software is a tool used to create visual representations of data. The video mentions that most graphing software can automatically generate a best fit line, which simplifies the process of data analysis. This software is essential in chemistry labs for plotting data and determining trends without manually calculating the best fit line.
💡Heat of Vaporization
The heat of vaporization is the amount of energy required to convert a substance from a liquid to a gas at a given pressure. In the script, it is shown how to calculate this value using the slope of a trendline and the known gas constant 'R'. This concept is used to demonstrate the application of graphing and linear equations in solving chemistry problems.
💡Units
Units are the measurements used to quantify physical properties. The video emphasizes the importance of labeling each axis with the appropriate units when graphing data. Units are crucial for ensuring that the data is interpreted correctly and for making accurate calculations, such as determining the slope or calculating the heat of vaporization.
💡Trendline Equation
The trendline equation is the mathematical formula that represents the best fit line on a graph. It is derived from the data points and is used to predict or calculate unknown values. In the video, the trendline equation is used to find the heat of vaporization by setting the slope equal to a specific term and solving for the unknown.
Highlights

In chemistry labs, understanding how to interpret and graph data is crucial for finding missing information.

Graphs consist of two axes: the horizontal x-axis (independent variable) and the vertical y-axis (dependent variable).

The x-axis represents the variable that can be controlled in an experiment, while the y-axis shows changes dependent on the x-axis.

Graphs should always include labels for both axes with units of measurement and a title indicating y vs. x.

Most chemistry graphs are linear, and data points are approximated using a 'best fit line' or 'trendline'.

Graphing software typically generates the best fit line for a set of data points.

The equation of a line is expressed as y = mx + b, where m is the slope and b is the y-intercept.

The y-intercept is a point on the y-axis, and the slope represents the rate of change of y over x.

The slope is particularly useful for determining unknown values in a chemical experiment.

To find the slope from two points, use the formula: (y2 - y1) / (x2 - x1).

Chemistry often involves using the coefficient in front of x from the trendline to find the slope, rather than manual calculation.

A well-constructed graph should include a title, labeled axes with units, a best fit line, and the trendline equation.

Chemistry formulas can represent the equation of a line, such as ln(P) = y, where P is vapor pressure and x is 1/T (temperature).

Graphing and determining the trendline equation can help find specific values, like the heat of vaporization.

The slope of the trendline can be used to calculate the heat of vaporization with the proper units and constants.

The units of the slope are determined by the x-axis variable, and constants like R (gas constant) are used in calculations.

To find the heat of vaporization, manipulate the trendline equation and solve for the desired value.

The final answer for the heat of vaporization is typically expressed in kilojoules after unit conversion.

Graphing is a fundamental skill in chemistry for solving a variety of problems and should be practiced thoroughly.

Transcripts

Browse More Related Video

4 Steps to Graphing Slope-Intercept Form | 8.EE.B.6 💗

Graphing Lines in Algebra: Understanding Slopes and Y-Intercepts

AP Physics 2023 Exam Solutions|Q2. PART A ( ii) | Complete Step-by-Step Answers and Explanations"

Graphing Lines in Slope-Intercept Form (y = mx + b)

The Main Ideas of Fitting a Line to Data (The Main Ideas of Least Squares and Linear Regression.)

Scatter Plots and Lines of Best Fit By Hand

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Chemistry LabData InterpretationGraph AnatomyBest Fit LineLinear EquationsSlope CalculationDensity FormulaHeat of VaporizationTrendline EquationScientific AnalysisLab TechniquesChemical Unknowns