Graphing Lines in Algebra: Understanding Slopes and Y-Intercepts
TLDRThe script explains the mathematical concepts of slope and y-intercept. It defines slope as the steepness of a line, calculated by rise over run between two points. Slope indicates the rate of change in the vertical direction. The y-intercept is where a line crosses the y-axis. Equations can be put in y=mx+b form, where m is the slope and b is the y-intercept. Slopes range from vertical lines with undefined slopes to horizontal lines with zero slopes. Any two points define a line and its slope. Understanding slopes and intercepts provides the foundation for graphing and analyzing lines.
Takeaways
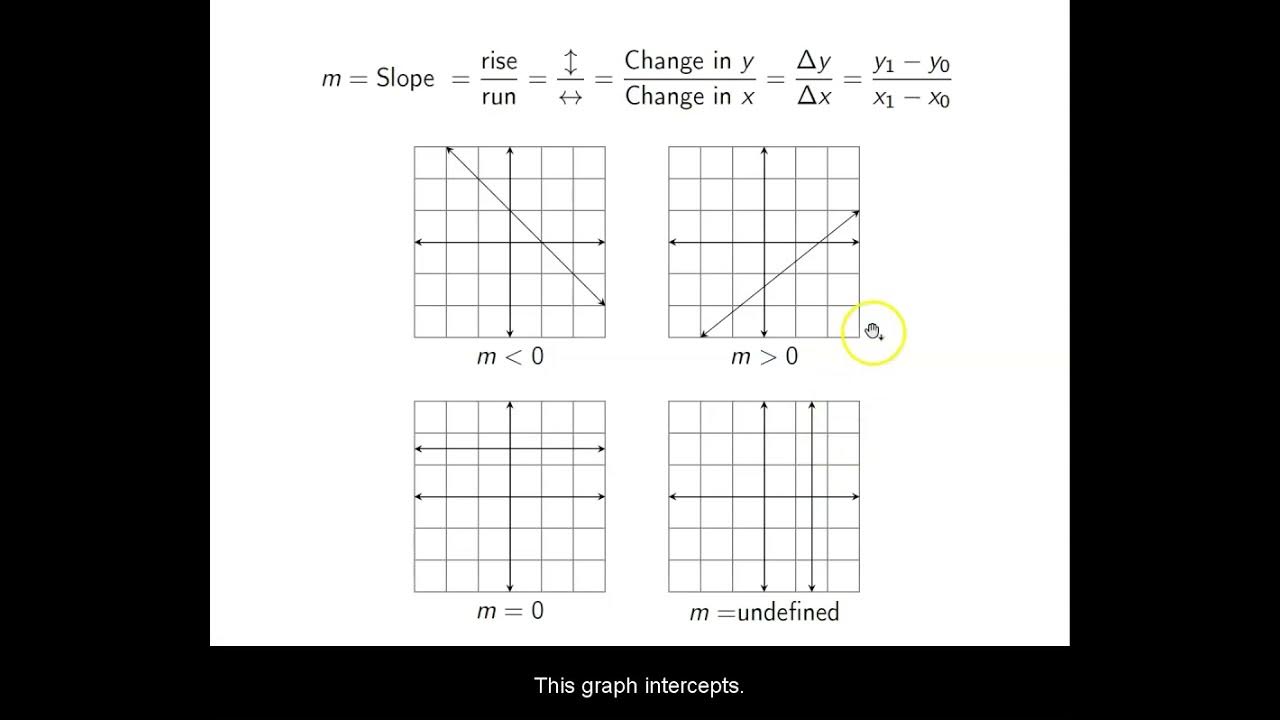
- 😀 Slope represents the steepness of a line and is calculated as rise over run (change in y over change in x).
- 😊 Vertical lines have an undefined slope, horizontal lines have a slope of 0.
- 🤔 Any two points define a line, but all lines contain infinite points between those two points.
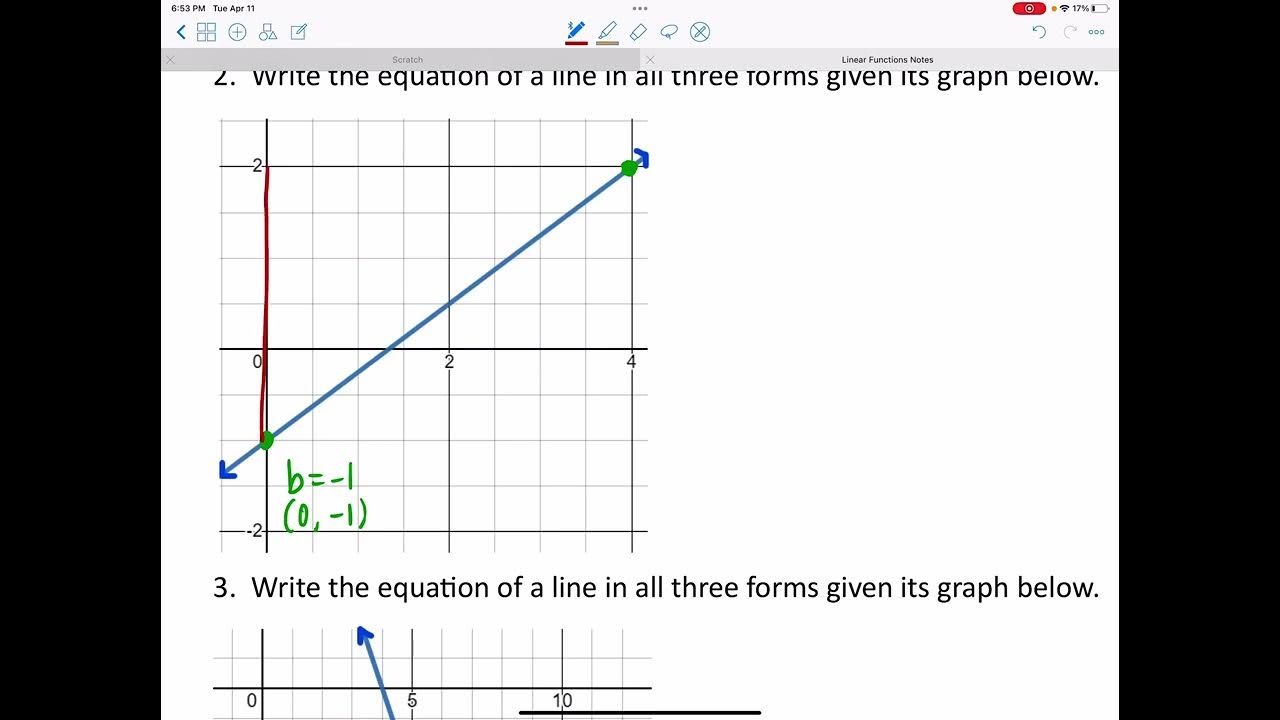
- 😮 The Y-intercept is the y value when x is 0, or where the line crosses the y axis.
- 🧐 To find the equation of a line, identify the slope and y-intercept.
- 👍 The slope remains constant along a given line.
- 😀 A slope greater than 1 indicates the line tilts upwards, less than 1 tilts downwards.
- 😟 When calculating slope, the x and y values for each point must stay together.
- 🤓 Negative slopes indicate the line runs positively but rises negatively.
- 🥳 Understanding slopes and intercepts provides the foundation for graphing linear equations.
Q & A
What does the slope of a line represent in math?
-The slope of a line represents the line's rate of change in the vertical direction. It indicates how steep or shallow the line is.
How is the slope of a line calculated?
-The slope of a line is calculated by finding the rise over the run. The rise represents the change in y-values and the run represents the change in x-values between two points on the line.
What is the slope of a horizontal line?
-A horizontal line has a slope of zero, because it runs infinitely along the x-axis without rising or falling.
What is the slope of a vertical line?
-A vertical line has an undefined slope, because it rises infinitely along the y-axis without any run along the x-axis.
What does the y-intercept represent?
-The y-intercept is the y-coordinate of the point where a line crosses the y-axis. It is represented by the B value in the equation y=mx+b.
What is the equation for a line with a slope of 2 and a y-intercept of 3?
-For a line with a slope of 2 and a y-intercept of 3, the equation would be y=2x+3.
How can you identify the slope and y-intercept from an equation?
-In the equation y=mx+b, m represents the slope and b represents the y-intercept. So you can identify them directly.
Do two points define a unique line?
-Yes, any two distinct points define a unique line that passes through both points.
Why does the order of points not matter when calculating slope?
-When calculating slope as rise over run, the order of the points does not matter because slope represents the rate of change, which is the same regardless of the direction traveled along the line.
What happens to slope as a line approaches vertical?
-As a line approaches being completely vertical, its slope approaches positive or negative infinity, eventually becoming undefined at exactly vertical.
Outlines
😀 Understanding Slope and Linear Equations
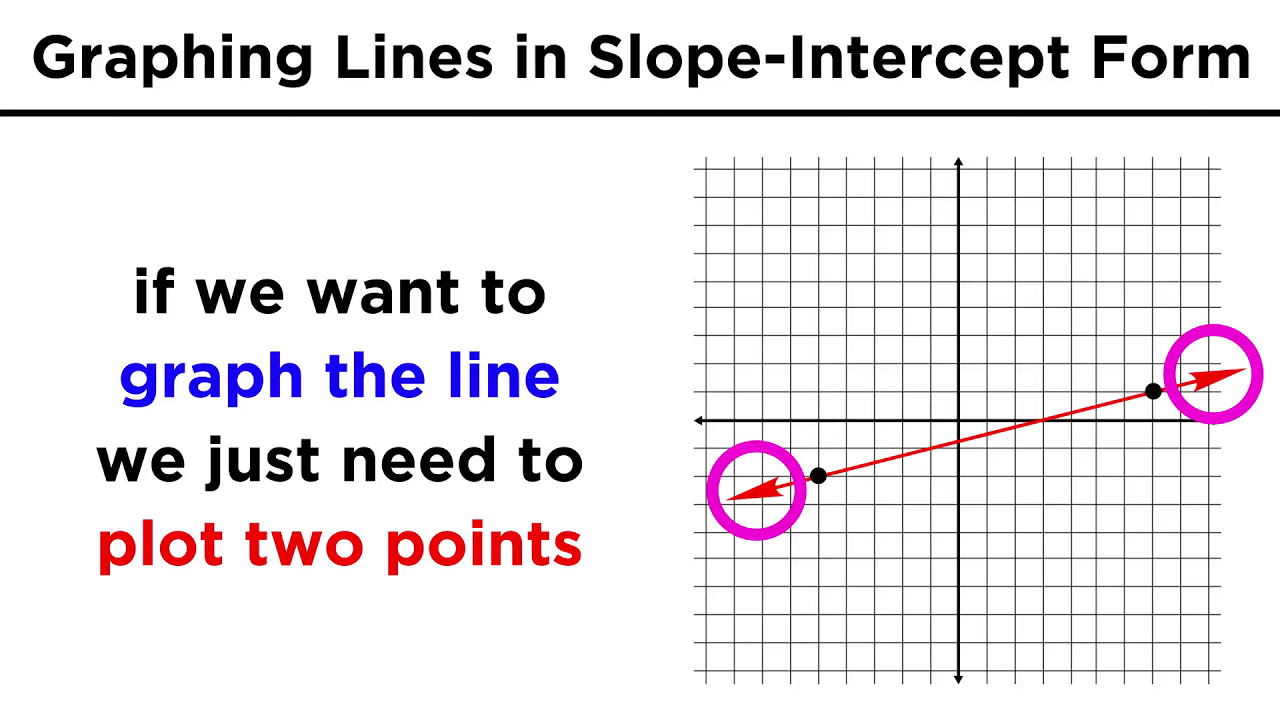
This paragraph introduces slope as the steepness of a line and rate of change in the vertical direction. It explains that slope (M) and y-intercept (B) are characteristics of a linear equation in the form Y=MX+B. Examples are given for lines with slopes of 1 and between 0 and infinity. Any two points define a line but all lines contain infinite points.
😃 Using Slope and Intercept to Graph Lines
This paragraph explains that one point and a slope can define a line. An example is given of graphing a line through (2,4) with slope 3/2. It emphasizes that slope represents the rate of change regardless of direction. The paragraph concludes by checking comprehension of slopes and y-intercepts.
Mindmap
Keywords
💡slope
💡Y-intercept
💡rise over run
💡vertical line
💡horizontal line
💡linear equation
💡coordinate plane
💡infinity
💡rate of change
💡undefined
Highlights
The study found that meditation can reduce stress and improve focus
Participants who meditated for 10 minutes daily saw improvements in attention span within 2 weeks
Meditation activates the prefrontal cortex, improving executive functioning
Mindfulness meditation specifically strengthened attentional stability and control
Meditation reduced anxiety and negative thinking patterns in participants
Regular meditation was linked to lower levels of the stress hormone cortisol
Study limitations include small sample size and reliance on self-reported data
More research is needed on optimal meditation techniques and duration
Meditation is a simple, accessible way to potentially improve cognition and reduce stress
Meditation could be integrated into schools and workplaces to enhance performance
Daily meditation may provide cognitive and mental health benefits for healthy adults
Meditation is not a cure-all but could be a helpful lifestyle practice for many
More randomized controlled trials with active control groups are needed
Future studies should investigate types of meditation and optimal duration/frequency
Meditation shows promise as an accessible and cost-effective intervention for cognition and stress
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: