Scatter Plots and Lines of Best Fit By Hand

pkkirkland
27 Jun 201206:50
EducationalLearning
32 Likes 10 Comments

TLDRThe video script outlines a step-by-step process for manually constructing a scatterplot from a given table of points and determining the line of best fit without the use of a calculator. It emphasizes the importance of identifying and ignoring outliers to ensure a strong correlation among the data points. The script then illustrates how to select two points from the trendline to derive the equation of the line, explaining the calculation of the slope and y-intercept. The final equation is presented in two forms, y = x + 2, demonstrating a practical approach to linear regression and highlighting the consistency of the slope and y-intercept in approximating the trendline.

Takeaways
  • 📊 The process begins with constructing a scatterplot from a table of points.
  • 🎯 After plotting the points, the next step is to find the line of best fit by hand without using a calculator.
  • 📝 Plotting involves placing each point on the coordinate plane according to its given coordinates.
  • 🔍 Identifying outliers is crucial; they should be ignored as they do not follow the general trend of the data.
  • 💪 A strong correlation in the data leads to a clearer line of best fit.
  • 🤔 Approximation is key when finding the line of best fit by hand, as it won't be perfectly accurate.
  • 🔢 The equation of a line is generally given by y = mx + b, where m is the slope and b is the y-intercept.
  • 📌 To find the slope (m), use the formula (y2 - y1) / (x2 - x1) with two selected points from the scatterplot.
  • 📝 Once the slope is determined, find the y-intercept (b) by substituting a point into the equation y = mx + b and solving for b.
  • 📈 The final equation of the line of best fit can be written in slope-intercept form (y = mx + b) or point-slope form.
  • 👀 Verify the equation by plugging in x values and checking if the corresponding y values match the plotted points.
Q & A

  • What is the primary focus of the video?

    -The primary focus of the video is to demonstrate how to construct a scatterplot from a table of points and then find the line of best fit by hand without using a calculator.

  • How does the speaker begin the process of constructing the scatterplot?

    -The speaker begins by plotting the given points on a coordinate plane, using the provided pair of numbers as coordinates for each point.

  • What is the significance of identifying outliers in the data set?

    -Identifying outliers is important because they do not follow the general trend of the data and can skew the line of best fit. In such cases, outliers should be ignored to obtain a more accurate representation of the data's trend.

  • How does the speaker approximate the line of best fit?

    -The speaker approximates the line of best fit by visually estimating a line that roughly goes through the middle of the plotted points, representing the strongest correlation within the data set.

  • What are the two key components needed to write the equation of a line?

    -The two key components needed to write the equation of a line are the slope (M) and the y-intercept (B).

  • How does the speaker choose the two points for finding the equation of the line?

    -The speaker chooses two points that seem reasonable and lie approximately on the visually estimated trend line. The choice can vary, but the goal is to pick points that best represent the overall trend without outliers.

  • What formula does the speaker use to calculate the slope of the line?

    -The speaker uses the slope formula (y2 - y1) / (x2 - x1), employing the values from the two selected points to calculate the slope.

  • How is the y-intercept (B) determined in the process?

    -The y-intercept (B) is determined by plugging one of the selected points into the equation y = mx + b and solving for B when y and x values are known.

  • What is the final equation of the line of best fit derived in the video?

    -The final equation of the line of best fit derived in the video is y = x + 2.

  • How does the speaker verify the approximated line of best fit?

    -The speaker verifies the approximated line of best fit by checking if the slope consistently goes up by 1 for every increase in x by 1, and if the y-intercept is approximately 2 when the x value is 0.

  • What is the main limitation of finding the line of best fit by hand?

    -The main limitation of finding the line of best fit by hand is that it cannot provide an exact or highly precise answer; it is an approximation that gives a reasonable solution without the use of a calculator.

Outlines
00:00
📊 Constructing a Scatterplot and Finding the Line of Best Fit

This paragraph explains the process of constructing a scatterplot from a table of points and finding the line of best fit without using a calculator. It begins with plotting the given points on a coordinate plane and then visually approximating a line that goes through the middle of these points to represent the best fit. The speaker acknowledges that this method is an approximation and may not be perfectly accurate. However, it serves the purpose of illustrating the concept and allows the selection of two points to determine the equation of the line. The points chosen are (7, 9) and (3, 5), and using these points, the speaker calculates the slope (M) and y-intercept (B) of the line. The slope is found by using the formula (y2 - y1) / (x2 - x1) and results in a value of 1. To find the y-intercept, one of the points is substituted into the equation y = mx + b, solving for b gives a value of 2. The final equation of the line of best fit is therefore y = x + 2, which is a simple linear equation reflecting a strong correlation between the points.

05:01
🔢 Using the Equation to Find a Specific Value

This paragraph focuses on applying the previously derived line equation to find the value of y when x is 9. The speaker reiterates the equation y = x + 2 and demonstrates how to plug in the x value to calculate the corresponding y value. By substituting x with 9 into the equation, the speaker calculates the y value to be 11, which is a reasonable approximation as it aligns with the trend observed in the scatterplot. The speaker emphasizes that this method is done by hand and is an approximation; more accurate results will be achieved using a calculator in future lessons. This paragraph reinforces the practical application of the line equation and the importance of understanding how to use it to make predictions or find specific values based on the established relationship between variables.

Mindmap
Keywords
💡Scatterplot
A scatterplot is a type of graphical representation used to display values for two variables for a set of data. In the video, the instructor explains how to construct a scatterplot from a table of points, which is essential for visualizing the relationship between two sets of data. The scatterplot is developed by plotting each point on a coordinate plane, allowing for the identification of trends or patterns within the data.
💡Line of Best Fit
The line of best fit, also known as the regression line, is a straight line that best represents the overall trend of a set of data points. It is used to summarize the relationship between two variables and make predictions. In the video, the instructor approximates this line by hand, drawing a line that roughly goes through the middle of the plotted points to represent the trend of the data.
💡Outlier
An outlier is an observation that significantly deviates from the other observations in a dataset. Outliers can skew the analysis and interpretation of data, so they are often identified and either adjusted or discarded. In the context of the video, the instructor mentions that if there was an outlier in the data, it would have to be ignored to accurately determine the line of best fit.
💡Correlation
Correlation refers to a statistical relationship between two variables that determines the strength and direction of the linear association between them. A strong correlation indicates that one variable is likely to change as the other variable changes. In the video, the instructor notes that the data has a strong correlation, which means there is a clear and consistent pattern between the points.
💡Trend Line
A trend line is a line that is drawn through a graph to represent the general trend or direction of the data. It helps in visualizing how the data points are moving and provides insight into future predictions. In the video, the instructor draws a trend line by hand to approximate the line of best fit, which represents the general trend of the data points.
💡Slope
The slope of a line is a measure of its steepness or the rate at which it inclines. It is calculated as the change in the y-values divided by the change in the x-values (rise over run). In the context of the video, the slope is determined by the difference in y-values (5 - 9) over the difference in x-values (3 - 7), which results in a slope of 1, indicating a one-to-one ratio of vertical to horizontal change.
💡Y-Intercept
The y-intercept is the point at which a line crosses the y-axis on a graph. It represents the value of y when x is equal to zero. In the video, the y-intercept is found by plugging in the x-value and the calculated slope into the equation of the line and solving for y. The y-intercept in this case is 2, which means the line crosses the y-axis at the point (0, 2).
💡Equation of a Line
The equation of a line is a mathematical representation that describes the relationship between two variables, typically denoted as y = mx + b, where m is the slope and b is the y-intercept. In the video, the instructor derives the equation of the line of best fit by finding the slope and y-intercept from the scatterplot data points, resulting in the equation y = x + 2.
💡Algebra
Algebra is a branch of mathematics that uses symbols and rules to solve equations and analyze mathematical structures. In the video, the instructor uses algebraic concepts and formulas to find the equation of the line of best fit, specifically employing the slope-intercept form of a linear equation, which is y = mx + b.
💡Calculator
A calculator is an electronic device used to perform mathematical calculations. In the video, the instructor mentions that while the process of finding the line of best fit and its equation is demonstrated by hand, the use of a calculator will be introduced in future lessons to improve the accuracy and efficiency of these calculations.
💡Estimation
Estimation is the process of approximating a value or quantity based on available data or information. In the context of the video, the instructor approximates the line of best fit by hand, which involves estimating where the line should be drawn to represent the data points accurately.
Highlights

The process of constructing a scatterplot from a table of points is discussed.

A method for finding the line of best fit without using a calculator is presented.

The importance of plotting points accurately on the coordinate plane is emphasized.

The concept of outliers and their impact on the line of best fit is introduced.

The strong correlation in the data leads to a clear line of best fit.

The selection of two points from the trendline to find the line's equation is explained.

The equation of a line (y = mx + b) is reviewed, where m is the slope and b is the y-intercept.

The calculation of the slope using the formula (y2 - y1) / (x2 - x1) is demonstrated.

The method for finding the y-intercept (b) by substituting a point into the equation is shown.

The final equation of the line of best fit is determined to be y = x + 2.

The practical application of the line's equation is illustrated by finding the y-value for a given x-value.

The approximation of the line by hand is acknowledged to have limitations.

The use of a calculator for more precise results is mentioned as a topic for future lessons.

The consistency of the slope in the context of the scatterplot is observed.

The approximate nature of the y-intercept is discussed in relation to the graph.

The process of finding the line of best fit is presented as a valuable tool for understanding data relationships.

Transcripts

Browse More Related Video

Calculating the equation of a regression line | AP Statistics | Khan Academy

Interpreting Graphs in Chemistry

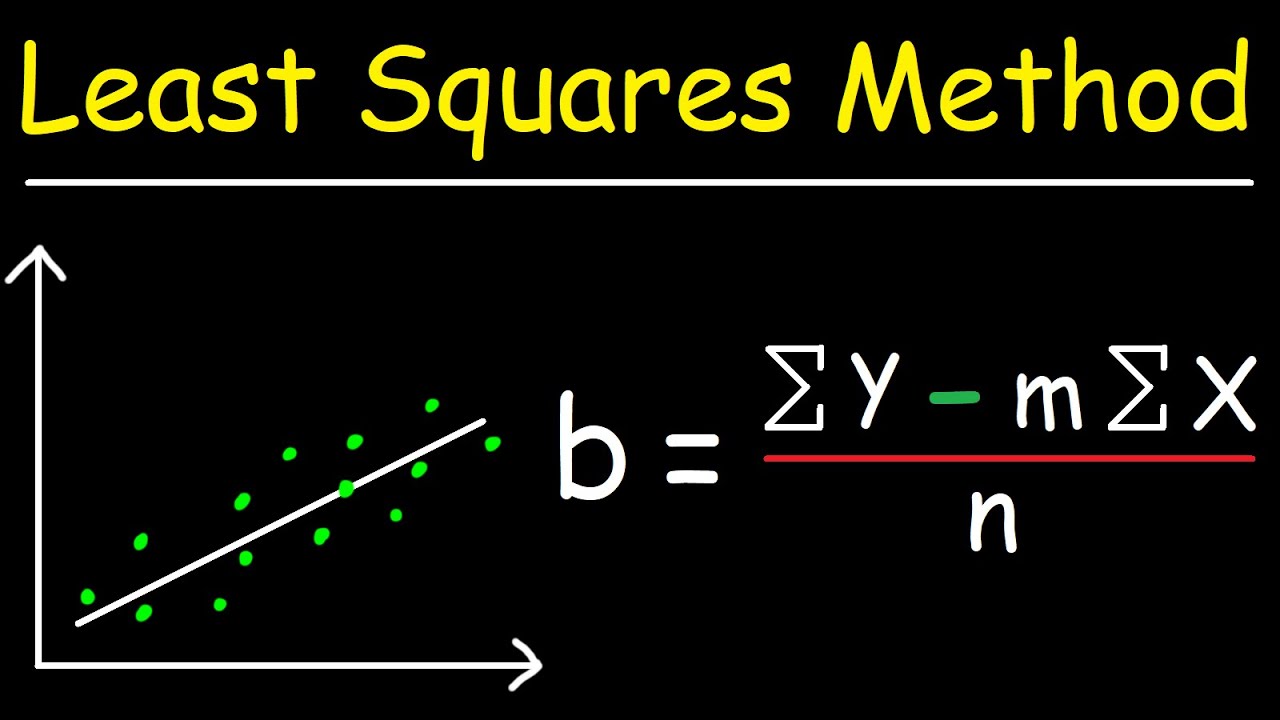
Linear Regression Using Least Squares Method - Line of Best Fit Equation

Graphing Lines in Slope-Intercept Form (y = mx + b)

Regression and R-Squared (2.2)

The Main Ideas of Fitting a Line to Data (The Main Ideas of Least Squares and Linear Regression.)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DataVisualizationScatterplotConstructionLineOfBestFitAlgebraMethodsMathematicsTutorialHandPlottingTrendlineEstimationCorrelationAnalysisBasicStatisticsEducationalContent