Intro to Derivatives, Limits & Tangent Lines in Calculus | Step-by-Step
TLDRThe video script delves into the application of calculus in determining the instantaneous velocity of an object, using the example of a rocket's ascent. It contrasts basic arithmetic problems involving constant speed with calculus's ability to handle varying velocities. The concept of average velocity is introduced as a starting point, showing how it's calculated over a period of time. However, the focus quickly shifts to finding the exact velocity at a specific point in time, which is where the power of limits in calculus becomes evident. The script guides through the process of progressively narrowing the time interval to get closer to the instantaneous velocity at a precise moment, T=2 seconds, for instance. This is achieved by taking the limit as T approaches the point of interest. The script concludes with a practical example using a simple function, f(T) = T^2, to find the velocity at T=1 second, illustrating the derivative concept and its relation to the slope of the tangent line on a position graph, which represents velocity. The lesson emphasizes the foundational role of limits and derivatives in calculus, essential for advanced problem-solving in fields like rocketry.
Takeaways
- 📈 The concept of velocity in calculus is different from basic arithmetic as it deals with the rate of change at a specific point in time, not an average over a period.
- 🚀 When analyzing the motion of an object like a rocket, calculus allows us to determine its velocity at any given moment, accounting for acceleration.
- 📊 The graph of an object's height versus time can show how the velocity changes, with a steeper curve indicating a higher velocity and a shallower curve indicating a lower velocity.
- 🔢 Average velocity is calculated by finding the distance traveled over a certain time period and is a starting point for understanding instantaneous velocity.
- 📌 The instantaneous velocity can be estimated by taking a very short time interval around the point of interest, which gives a more accurate approximation of the velocity at that point.
- 🤔 Calculus uses limits to find the exact velocity at a specific point in time, which is a concept that allows us to get infinitely close to the exact moment we're interested in.
- 🧮 The limit definition of the derivative is used to find the instantaneous velocity, which is the slope of the tangent line to the position function at a given point.
- 📐 In the context of the rocket example, as the rocket gets lighter, it accelerates and thus its velocity increases, which is represented by the steepening of the curve on the position-time graph.
- 🛫 For an object moving at a constant speed, the position-time graph would be a straight line, indicating a constant velocity with no acceleration.
- 💡 Understanding the concept of limits is crucial for grasping calculus, as it enables the calculation of quantities that are constantly changing, such as velocity in motion.
- 📚 The process of finding the instantaneous velocity involves a transition from average velocity to a more precise value by continuously narrowing the time interval around the point of interest.
Q & A
What is the main difference between basic arithmetic and calculus when dealing with velocity?
-In basic arithmetic, we deal with average velocity, which is the total distance divided by the total time. In calculus, we focus on instantaneous velocity, which is the velocity at a specific point in time, taking into account the changing nature of motion.
Why does the velocity of a rocket not remain constant as it ascends?
-The velocity of a rocket does not remain constant because as the rocket burns fuel and loses mass, it accelerates. This results in an increase in velocity as the rocket gets lighter and the thrust provided by the engines remains the same or increases.
How is the concept of a tangent line related to the velocity of an object in calculus?
-The concept of a tangent line in calculus is related to velocity because the slope of the tangent line to the position function of an object at a specific point in time represents the instantaneous velocity of the object at that point.
What is the formula for calculating the instantaneous velocity of an object at a specific time T naught?
-The formula for calculating the instantaneous velocity (v) at a specific time T naught is v = lim (as T approaches T naught) [(f(T) - f(T naught)) / (T - T naught)] where f(T) is the position function of the object.
Why do we use limits in calculus to find the instantaneous velocity?
-We use limits in calculus to find the instantaneous velocity because they allow us to get infinitely close to the exact point in time we are interested in, thus providing an exact value for the velocity at that specific moment, rather than an average over a period of time.
What is the significance of the position function being t squared in the given example?
-The position function being t squared signifies that the object's height with respect to time is directly proportional to the square of the time, indicating a constant acceleration (as in the case of an object in free fall or a rocket under constant thrust).
How does the concept of limits allow us to calculate the velocity of a rocket at a precise moment?
-The concept of limits allows us to calculate the velocity of a rocket at a precise moment by enabling us to take an infinitesimally small time interval around the point of interest. This effectively gives us the instantaneous rate of change of position, which is the definition of velocity at that point.
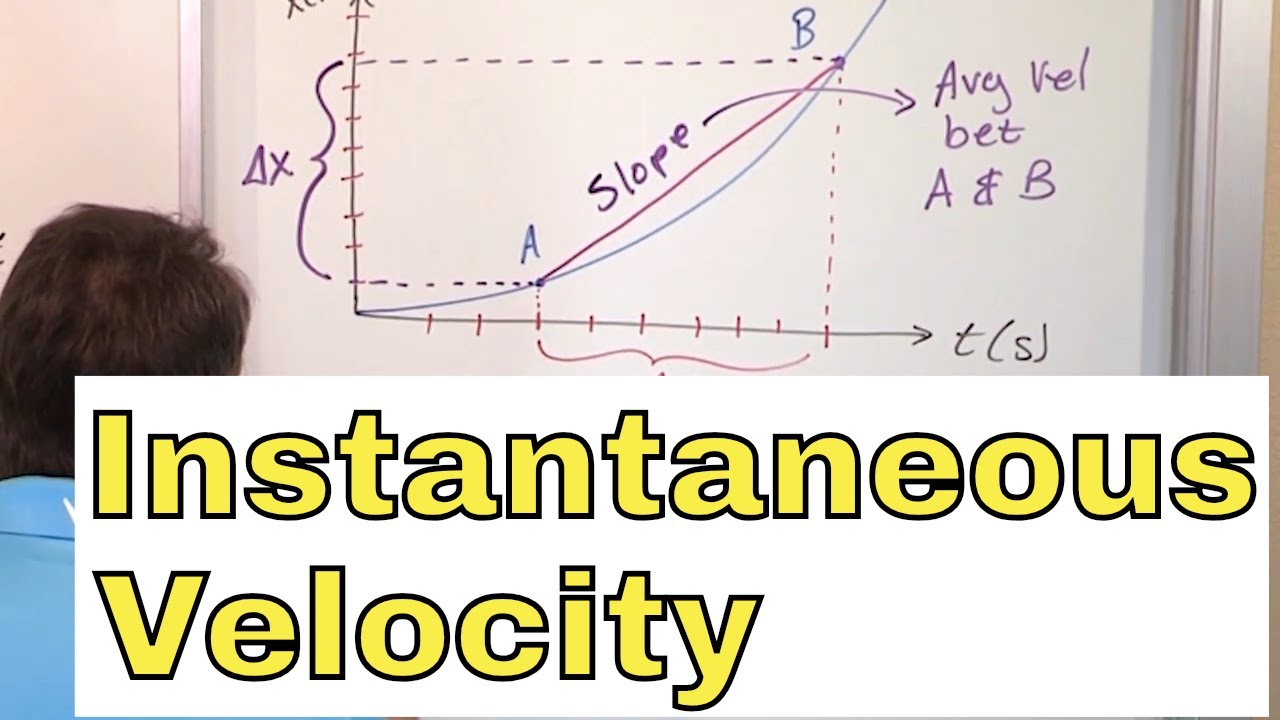
What is the role of the slope in understanding the velocity from a graphical perspective?
-The slope of the line connecting two points on the position-time graph represents the average velocity over that interval. As we narrow down the interval to approach a single point, the slope of the tangent to the curve at that point represents the instantaneous velocity.
Why is calculus essential for designing and understanding the motion of objects like rockets?
-Calculus is essential for designing and understanding the motion of objects like rockets because it provides the mathematical tools to handle variable motion, such as acceleration. It allows for the precise calculation of velocities at any given time, which is crucial for trajectory planning and engine performance analysis.
What is the practical application of finding the instantaneous velocity of a rocket at a specific time?
-The practical application of finding the instantaneous velocity of a rocket at a specific time includes optimizing the burn rate of the fuel, ensuring the rocket reaches the desired speed at critical phases of the launch, and making real-time adjustments for course corrections or to meet mission-specific velocity requirements.
How does the process of taking a limit in calculus help us in real-world scenarios where we deal with continuously changing quantities?
-The process of taking a limit in calculus helps us in real-world scenarios by allowing us to find exact values of quantities that are changing continuously. This is particularly useful in physics and engineering, where we often need to determine rates of change, such as velocities, accelerations, or rates of growth, at specific points in time.
Outlines
🚀 Understanding Velocity in Calculus
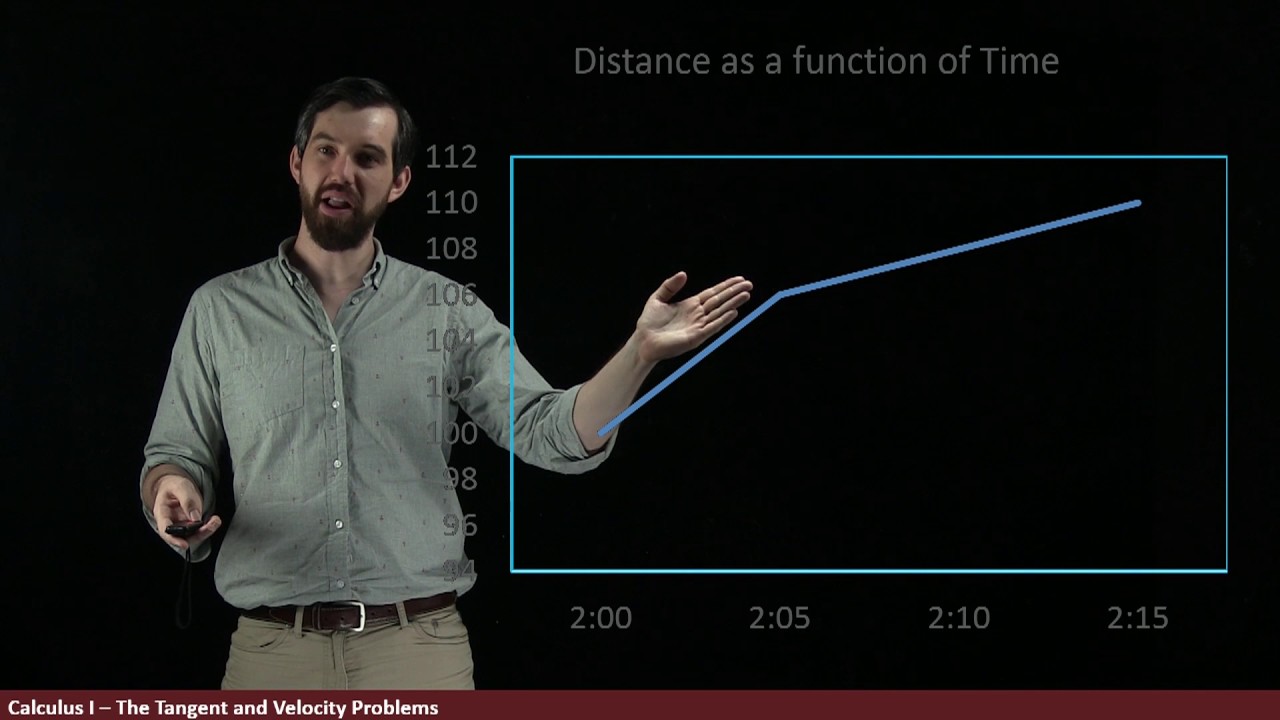
This paragraph introduces the concept of velocity in calculus, contrasting it with basic arithmetic where average velocity is sufficient. It explains that in calculus, we're interested in the instantaneous velocity at a specific point in time, not just an average. The example of a rocket ship is used to illustrate how velocity changes over time as it ascends, getting lighter and thus accelerating. The concept of a position function over time is introduced, and the difference between constant velocity (a straight line graph) and changing velocity (a curved graph) is explained. The paragraph concludes by emphasizing the need to calculate instantaneous velocity at a point, not just an average, which leads into the concept of limits.
📏 Calculating Average and Instantaneous Velocity
This paragraph delves deeper into how to calculate the velocity of an object like a rocket. It starts by explaining average velocity as distance traveled divided by time taken, using the rocket's position function over time as an example. The concept of using two points to estimate velocity is introduced, with the understanding that as the time interval gets smaller, the estimate becomes more accurate. The paragraph also touches on the geometric interpretation of velocity as the slope of the position function graph. It concludes by emphasizing that while these are crude approximations, they serve as a foundation for understanding the more precise concept of limits in calculus.
🎯 Applying Limits to Find Exact Velocity
The paragraph focuses on the application of limits to find the exact velocity of an object at a specific point in time. It discusses the limitations of using only two points to estimate velocity and how using limits allows us to get infinitely close to the exact point of interest. The concept of the instantaneous velocity at a point T is introduced, and the formula for calculating it using a limit is presented and explained. The paragraph emphasizes the importance of limits in calculus and how they enable us to find exact values in continuously changing situations.
🔍 Refining the Velocity Calculation with Closer Points
This paragraph builds on the previous one by showing how to refine the calculation of velocity by choosing points closer and closer to the point of interest. It visually demonstrates how narrowing the time interval between the points used in the calculation results in a better approximation of the instantaneous velocity. The concept of taking a limit as this interval approaches zero is reiterated, highlighting that this process allows us to find the exact velocity at a specific point on the graph, which is a fundamental aspect of calculus.
🧮 Practical Application: Finding Velocity with a Given Function
The paragraph provides a practical example of calculating velocity using the limit concept. It presents a specific function for the rocket's height over time (t squared) and walks through the steps to find the velocity at one second. The process involves substituting the function into the limit formula, simplifying the expression, and solving the limit to find the velocity in meters per second. This example solidifies the understanding of how calculus can be used to solve real-world problems involving changing quantities.
🏗️ The Foundation of Calculus: Limits and Derivatives
In the final paragraph, the broader significance of the limit concept in calculus is discussed. It emphasizes that limits are crucial for dealing with continuously changing quantities, which is a common theme in calculus. The paragraph recaps the process of finding average and instantaneous velocity and connects it to the concept of derivatives, which are the foundation of calculus. It concludes by encouraging students to understand the importance of limits as they move forward in their study of calculus.
Mindmap
Keywords
💡Velocity
💡Average Velocity
💡Instantaneous Velocity
💡Position Function
💡Limit
💡Derivative
💡Tangent Line
💡Rocket Trajectory
💡Slope
💡Calculus
💡Acceleration
Highlights
Calculus is used to determine the velocity of an object at a specific point in time, which is essential for understanding the motion of objects like rockets.
The concept of average velocity is a starting point in calculus, but it is not sufficient for precise calculations at a given moment.
The velocity of an object like a rocket is not constant; it increases as the rocket gets lighter and accelerates.
The position graph of an object's motion can be used to estimate its velocity at different points by examining the slope of the graph.
In calculus, the instantaneous velocity at a specific point is found by taking a limit as the time interval approaches zero.
The slope of the tangent line to the position graph at a given point represents the velocity of the object at that point.
The process of finding the instantaneous velocity involves selecting points closer and closer to the point of interest and calculating the average velocity between them.
The limit concept is fundamental to calculus, allowing for the calculation of exact values at a specific point where direct measurement is not possible.
The velocity of a rocket at a specific time can be calculated using the limit of the position function as time approaches that specific point.
The general formula for finding the instantaneous velocity at a point T naught is given by the limit as T approaches T naught of (f(T) - f(T naught)) / (T - T naught).
An example problem demonstrates the calculation of the velocity of a rocket at one second using the given position function f(T) = T squared.
The technique of using limits to find instantaneous velocity is a foundational concept of calculus and is applicable to various real-world problems.
The concept of a derivative, which is introduced later in calculus, is closely related to finding the slope of the tangent line to a curve, which represents velocity.
The ability to calculate instantaneous velocity is crucial for advanced fields like rocketry, where precise measurements are necessary for success.
The process of using limits to find instantaneous velocity involves a series of approximations that become increasingly accurate as they get closer to the point of interest.
The final calculation of velocity at a specific time involves solving a limit problem, which simplifies to finding the derivative of the position function at that time.
The understanding of limits and their application in calculus is a significant intellectual breakthrough that has wide-ranging implications in mathematics and physics.
Transcripts
Browse More Related Video

Average/Instantaneous Rates of Changes
07 - What is Instantaneous Velocity?, Part 1 (Instantaneous Velocity Formula & Definition)

The Velocity Problem | Part I: Numerically
The Velocity Problem | Part II: Graphically

Understanding Differentiation Part 2: Rates of Change

Worked example: Motion problems with derivatives | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: