The Velocity Problem | Part I: Numerically

Dr. Trefor Bazett
5 Aug 201707:52
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of calculus through the 'velocity problem'. It begins with a scenario where a driver is at a certain mile marker at 2:00 PM and at another mile marker by 2:15 PM, prompting the question of the driver's speed. The script explains the difference between average velocity, calculated over a time interval, and instantaneous velocity, which is the speed at a specific moment. The average velocity is computed as the change in distance divided by the change in time. However, to find the speed at an exact moment, such as 2:15 PM, the concept of instantaneous velocity is introduced. This is illustrated by considering smaller and smaller time intervals, leading to the idea of a limiting process. The script also touches on how modern lidar guns used by police work, which measure speed by calculating the average velocity over very small time intervals. This process is crucial for understanding the instantaneous velocity at a precise moment.

Takeaways
  • πŸš— The concept of 'velocity' is central to the investigation of calculus, with a focus on understanding how fast an object is moving at a given time or over a period.
  • ❓ The question 'how fast am I going?' requires clarification on whether it's about speed at a specific moment or over an interval.
  • πŸ“ 'Average velocity' is calculated by dividing the change in distance (Ξ”D) by the change in time (Ξ”T), providing an overall rate of motion over a period.
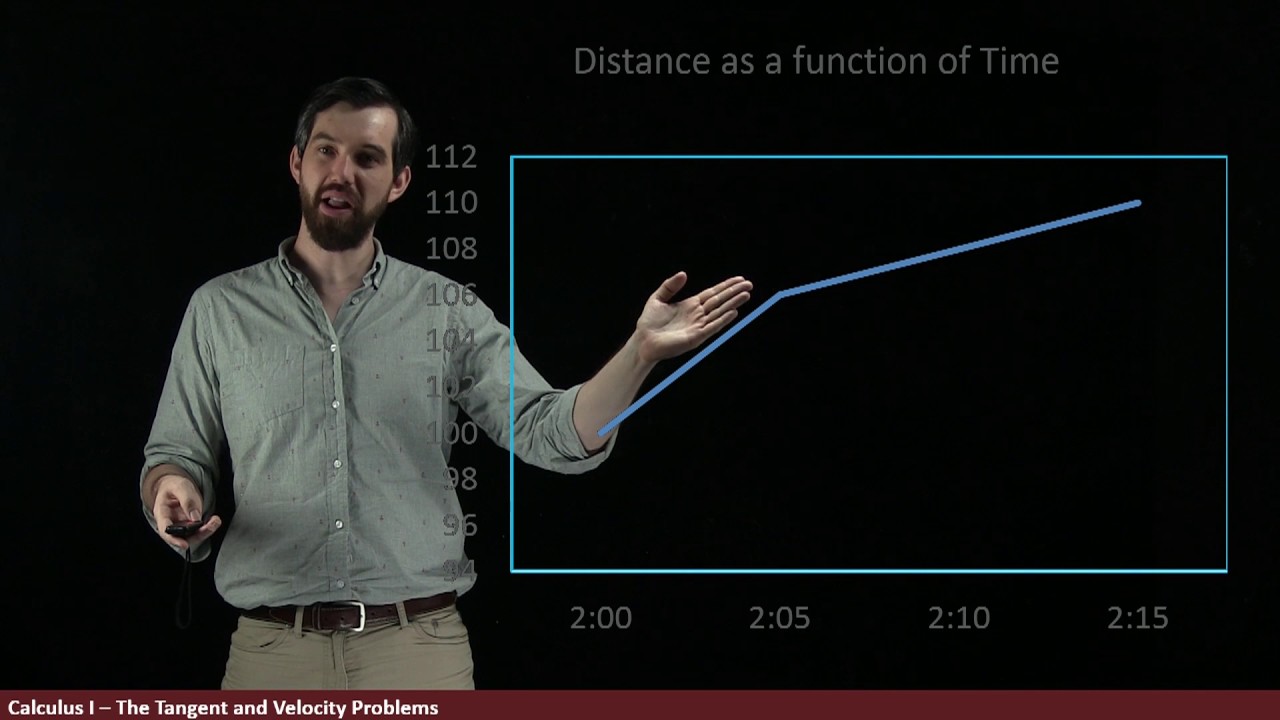
  • πŸ•’ The example given involves driving from a 100-mile marker to a 110-mile marker in 15 minutes, resulting in an average velocity calculation.
  • πŸ”’ After calculating the average velocity as 10 miles in 50 minutes, a unit conversion is applied to express the speed in miles per hour (mph).
  • 🚦 The average velocity of 40 mph over 15 minutes doesn't necessarily reflect the speed at any given second, such as at 2:15 precisely.
  • 🚨 A police officer measuring speed is interested in 'instantaneous velocity', which is the speed at a specific moment, not an average over a period.
  • πŸ“‰ The idea of 'limiting process' is introduced to find the instantaneous velocity by considering smaller and smaller time intervals.
  • πŸ”¬ Modern lidar guns used by police measure speed by taking rapid, successive measurements of the distance between the officer and the car, effectively calculating the average velocity over very small time intervals.
  • 🏎️ The instantaneous velocity can be understood as the limit of the average velocities as the time intervals approach zero.
  • πŸ’‘ The importance of computing average velocities in the limit of very small time intervals is emphasized for accurately determining instantaneous velocity.
Q & A

  • What is the 'velocity problem' in the context of calculus?

    -The 'velocity problem' is a scenario used to introduce the concept of velocity in calculus. It involves a person driving down a highway and provides a situation to explore the difference between average velocity and instantaneous velocity.

  • How is average velocity calculated?

    -Average velocity is calculated as the change in distance (Ξ”d) divided by the change in time (Ξ”t). It represents the total distance traveled divided by the total time taken over a specific interval.

  • What is the formula for average velocity in mathematical notation?

    -The formula for average velocity in mathematical notation is Ξ”V = Ξ”d / Ξ”t, where Ξ”V is the change in velocity, Ξ”d is the change in distance, and Ξ”t is the change in time.

  • Why might the speed given in miles per minute not be typical for everyday use?

    -Speeds are typically given in miles per hour because it is a more conventional unit of time for measuring speed over longer distances or durations, which is common in everyday driving scenarios.

  • How can you convert the average velocity from miles per minute to miles per hour?

    -To convert the average velocity from miles per minute to miles per hour, you multiply the velocity in miles per minute by 60, since there are 60 minutes in an hour.

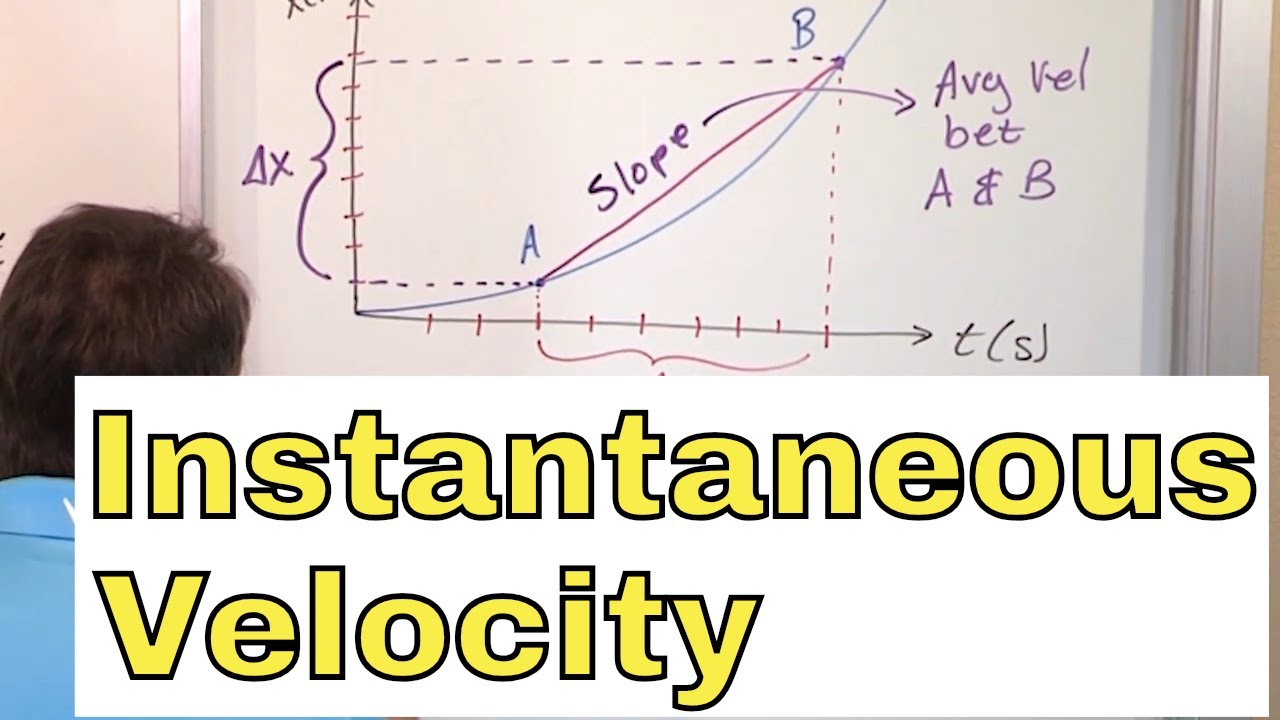
  • What is the difference between average velocity and instantaneous velocity?

    -Average velocity is the total distance traveled divided by the total time taken over an interval, while instantaneous velocity is the speed of an object at a specific moment in time. Instantaneous velocity can be thought of as the limit of the average velocity as the time interval approaches zero.

  • How does a police officer measure instantaneous velocity using a radar gun?

    -A police officer can measure instantaneous velocity using a radar gun by sending out pulses of light and measuring the time it takes for the light to reflect back from the car. By calculating the distance the car has traveled between two very close time intervals, they can determine the instantaneous velocity.

  • What is the concept of a limiting process in the context of instantaneous velocity?

    -The concept of a limiting process in the context of instantaneous velocity involves taking the average velocity over smaller and smaller time intervals, approaching the specific moment in time for which the instantaneous velocity is desired. As the time interval approaches zero, the average velocity approaches the instantaneous velocity.

  • How do modern lidar guns work to measure a vehicle's speed?

    -Modern lidar guns work by sending out rapid pulses of light and measuring the time it takes for the light to reflect back from the vehicle. By calculating the distance traveled by the vehicle between these very short time intervals, the gun can compute an average velocity that approximates the instantaneous velocity.

  • Why is it important to calculate average velocities over very small time intervals when measuring instantaneous velocity?

    -Calculating average velocities over very small time intervals allows for a more accurate approximation of the instantaneous velocity. As the time interval decreases, the average velocity over that interval becomes a better estimate of the speed at a specific moment in time.

  • What is the practical application of understanding the difference between average and instantaneous velocity?

    -Understanding the difference between average and instantaneous velocity is crucial in various fields, including physics, engineering, and everyday scenarios like driving. It helps in accurately measuring speed at a specific moment, which is important for traffic enforcement, race car performance, and scientific experiments.

  • How can the concept of instantaneous velocity be applied in physics to describe the motion of objects?

    -In physics, the concept of instantaneous velocity is applied to describe the motion of objects at a precise point in time or space. It is a fundamental concept in deriving equations of motion and understanding phenomena such as acceleration, projectile motion, and the behavior of particles in a system.

Outlines
00:00
πŸš— Understanding Average and Instantaneous Velocity

The first paragraph introduces the concept of calculus through a real-world scenario known as the velocity problem. It explores the question of how to determine the speed of a car at a specific time, emphasizing the difference between average velocity over a time interval and instantaneous velocity at a precise moment. The average velocity is calculated by dividing the change in distance by the change in time, which in this case is found to be 40 miles per hour over a 15-minute interval. The paragraph also discusses how a police officer might measure velocity at a specific time, which would be the instantaneous velocity. It concludes with the idea that to find the instantaneous velocity, one would look at increasingly smaller time intervals, a concept that modern lidar guns used by police employ to measure speed.

05:03
πŸ” Instantaneous Velocity and Limiting Processes

The second paragraph delves deeper into the concept of instantaneous velocity by using the analogy of a limiting process. It describes how by examining average velocities over smaller and smaller time intervals, one can approximate the instantaneous velocity at a specific time, such as 2:15 PM. The paragraph provides an example of how a police officer might use data from a table of average velocities to determine that a car is traveling at a speed close to 60 miles per hour at a particular second. It explains that modern lidar guns function by sending out rapid pulses of light to measure the change in distance over an extremely small time interval, allowing for the calculation of average velocity and thus obtaining an accurate measurement of the car's speed. The paragraph concludes by emphasizing the importance of computing average velocities as the time intervals approach zero to determine the instantaneous velocity.

Mindmap
Keywords
πŸ’‘Velocity Problem
The velocity problem is a scenario used in the video to introduce the concept of calculus. It involves a driver who is at a certain location at a specific time and is expected to be at another location at a later time. The problem is to determine the driver's speed. This scenario is central to the video's theme as it sets the stage for discussing the difference between average velocity and instantaneous velocity.
πŸ’‘Average Velocity
Average velocity is defined as the total distance traveled divided by the total time taken. In the context of the video, it is calculated by the change in distance (from mile marker 100 to 110) divided by the change in time (from 2:00 to 2:15). This concept is crucial as it is the first method introduced for determining how fast the driver is going over a given time interval.
πŸ’‘Instantaneous Velocity
Instantaneous velocity refers to the speed of an object at a specific moment in time, as opposed to the average velocity over a period. The video illustrates this by considering smaller and smaller time intervals around the time of interest (2:15). This concept is key to understanding how a police officer might measure speed using a radar gun, which takes very short time intervals to calculate velocity.
πŸ’‘Time Interval
A time interval is a span of time between two points. In the video, the time interval is initially 15 minutes (from 2:00 to 2:15) for calculating average velocity. As the discussion progresses, the concept of taking increasingly smaller time intervals is introduced to approach the concept of instantaneous velocity. This is vital for the narrative as it bridges the gap between average and instantaneous velocity.
πŸ’‘Mile Marker
A mile marker is a sign or marker along a road that indicates the distance traveled. In the script, the driver is said to be at the 100-mile marker at 2:00 and expected to be at the 110-mile marker at 2:15. Mile markers are used in the video to establish the distance traveled, which is necessary for calculating both average and instantaneous velocity.
πŸ’‘Unit Conversion
Unit conversion is the process of changing the units of measurement. In the video, the average velocity initially calculated in miles per minute is converted to miles per hour by multiplying by 60 (the number of minutes in an hour). This conversion is important because it provides the speed in a more conventional unit, making it easier to understand and compare to speed limits.
πŸ’‘Limiting Process
A limiting process in calculus involves taking a mathematical sequence or function to its limit as an input approaches a certain value. In the context of the video, the limiting process is used to describe how to find the instantaneous velocity by considering average velocities over smaller and smaller time intervals approaching the specific time of interest.
πŸ’‘Lidar Guns
Lidar guns, or Light Detection and Ranging devices, are used by police to measure the speed of vehicles. The video explains that these devices work by sending out pulses of light and calculating the time it takes for the light to reflect back from the vehicle, which allows for the determination of speed. Lidar guns are an example of how the concept of instantaneous velocity is applied in real-world scenarios.
πŸ’‘Speed Limit
The speed limit is the maximum legal speed at which vehicles are permitted to travel on a road. The video uses the concept of the speed limit to illustrate the practical implications of calculating instantaneous velocity, particularly when a driver might be ticketed for speeding if the measured velocity exceeds the speed limit.
πŸ’‘Distance Change
Distance change refers to the difference in distance between two points. In the video, the distance change is from the 100-mile marker to the 110-mile marker, which is used to calculate the average velocity. Understanding distance change is fundamental to the concept of velocity, as it represents the 'space' component in the space-time relationship.
πŸ’‘Time Change
Time change is the difference in time between two events. In the context of the video, the time change is from 2:00 to 2:15, which is used to calculate the average velocity. Time change is essential in calculus and physics as it represents the 'time' component in the space-time relationship and is necessary for determining rates of change, such as velocity.
Highlights

Investigation of calculus begins with the velocity problem, a practical scenario involving driving and speed.

The concept of 'how fast' is explored, emphasizing the need for precision in defining the term 'speed'.

Introduction to average velocity, calculated as the change in distance divided by the change in time.

Mathematical notation is used to express the formula for average velocity (Ξ”V/Ξ”T).

A 15-minute time interval is used to compute the average velocity, resulting in 40 miles per hour.

Unit conversion from miles per minute to miles per hour is demonstrated for practical speed measurement.

The difference between average velocity over an interval and instantaneous velocity at a specific time is discussed.

A hypothetical scenario where a police officer measures speed at a specific time, raising questions about the nature of velocity measurement.

The concept of instantaneous velocity is introduced as a limiting process of average velocities over increasingly smaller time intervals.

Modern lidar guns used by police are explained as a practical application of measuring instantaneous velocity.

Lidar technology operates by sending out pulses of light to measure the distance between the cop and the car over tiny time intervals.

The process of computing average velocities over very small time intervals is key to achieving an accurate speed measurement.

The transcript explores the theoretical underpinnings of how speed is measured in real-world applications.

The importance of precise measurement in understanding the difference between average and instantaneous velocity is emphasized.

The practical implications of velocity measurement are highlighted, especially in the context of traffic enforcement.

The discussion provides a clear understanding of the mathematical and physical principles behind speed calculations.

The use of real-world examples helps to contextualize the abstract concepts of calculus within a familiar scenario.

The transcript concludes with an emphasis on the importance of the limiting process in calculating instantaneous velocity.

Transcripts

Browse More Related Video

Understanding Differentiation Part 2: Rates of Change

Intro to Derivatives, Limits & Tangent Lines in Calculus | Step-by-Step

07 - What is Instantaneous Velocity?, Part 1 (Instantaneous Velocity Formula & Definition)

The Velocity Problem | Part II: Graphically

Average/Instantaneous Rates of Changes

Lecture 02: Stop Sign Crime The First Idea of Calculus The Derivative

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusVelocityAverage VelocityInstantaneous VelocityDriving ScenarioSpeed MeasurementLimiting ProcessLidar TechnologyPhysicsMathematicsEducational Content