Limits of Inverse Trigonometric Functions | Calculus

The Organic Chemistry Tutor
5 Jan 202013:16
EducationalLearning
32 Likes 10 Comments

TLDRThis transcript delves into the concept of limits in calculus, specifically focusing on inverse trigonometric functions. It explains how the graph of the inverse tangent function has two horizontal asymptotes and demonstrates that the limit of the inverse tangent function approaches pi/2 as x approaches positive infinity and -pi/2 as x approaches negative infinity. The transcript further explores the limits of other inverse trigonometric functions, such as arc cosine and arc sine, and provides examples of how to evaluate them. It emphasizes the importance of understanding the graph's behavior and the concept of one-sided limits in solving these problems.

Takeaways
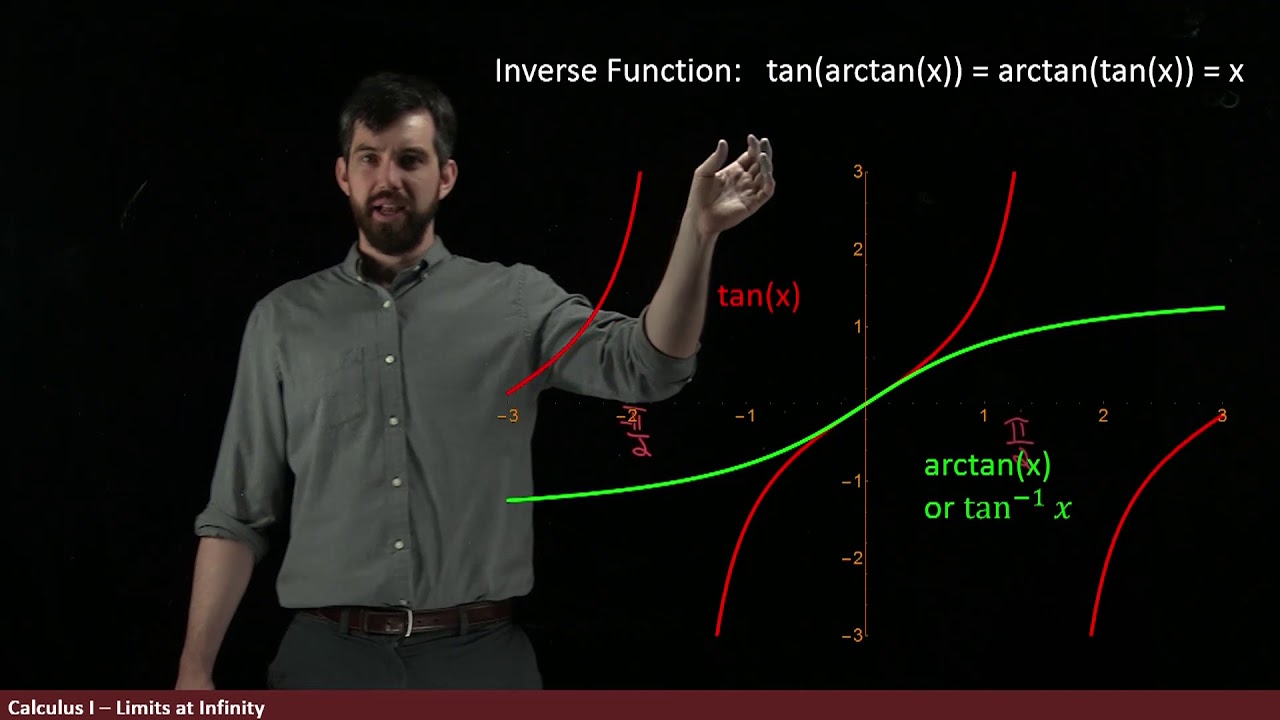
  • ๐Ÿ“ˆ Understanding the graph of the inverse tangent (arctan) is crucial for determining limits as x approaches infinity or negative infinity, with the function approaching ฯ€/2 and -ฯ€/2 respectively.
  • ๐Ÿšซ When evaluating limits of inverse trigonometric functions, direct substitution may not always be possible, and one-sided limits or alternative methods may be required.
  • ๐Ÿ”ข For the function arctan(x) as x approaches 2 in the example given, the limit does not exist because the left-sided limit approaches negative infinity and the right-sided limit approaches positive infinity.
  • ๐Ÿ“Š The graph of 1/x has a vertical asymptote at x=0 and a horizontal asymptote of y=0, leading to the limit of arccos(1/x) as x approaches infinity being 0, or equivalently, arccos(0) which is ฯ€/2.
  • ๐Ÿฅ‡ The domain and range of arc cosine (arccos) are from -1 to 1 and 0 to ฯ€, respectively, which helps in understanding the behavior of the function as x approaches its limits.
  • ๐Ÿงฎ For the expression arcsin(5 + 2x^3 / (4x^3 - 8)), simplifying the limit as x approaches infinity involves multiplying the numerator and denominator by 1/x^3 and results in the arc sine of 1/2, which is ฯ€/6.
  • ๐Ÿ“ The domain of arcsine (arcsin) is -1 to 1, and the range is -ฯ€/2 to ฯ€/2, which is important for determining the validity of the function's output.
  • ๐ŸŒ When dealing with inverse trigonometric functions, it's beneficial to visualize the graphs and understand their asymptotic behavior for solving limit problems.
  • ๐Ÿ”„ The process of finding limits often involves breaking down expressions and analyzing their behavior as they approach specific values or infinity.
  • ๐Ÿ“– Memorizing the shapes of the graphs of inverse trigonometric functions can greatly simplify the process of evaluating limits in calculus problems.
Q & A

  • What is the limit of the inverse tangent function as x approaches infinity?

    -The limit of the inverse tangent function as x approaches infinity is pi/2.

  • What are the two horizontal asymptotes for the graph of the inverse tangent function?

    -The two horizontal asymptotes for the graph of the inverse tangent function are y = pi/2 and y = -pi/2.

  • How does the graph of the inverse tangent function behave as x approaches negative infinity?

    -As x approaches negative infinity, the graph of the inverse tangent function approaches the horizontal asymptote y = -pi/2.

  • Why can't direct substitution be used to find the limit of arc tangent of (1/x - 2) as x approaches 2?

    -Direct substitution cannot be used because it results in an undefined expression with a 0 in the denominator when x equals 2.

  • What do one-sided limits indicate in the context of the function arc tangent of (1/x - 2) as x approaches 2?

    -One-sided limits indicate the behavior of the function as it approaches the given value from either the left or the right, which can differ in this case, leading to the conclusion that the original limit does not exist.

  • What is the limit of the expression 1/x as x approaches infinity in the context of the function arc cosine of (1/x)?

    -The limit of the expression 1/x as x approaches infinity is 0, which corresponds to the arc cosine of 0, yielding a result of pi/2.

  • How does the graph of the function 1/x behave as x approaches infinity?

    -As x approaches infinity, the graph of the function 1/x approaches a y-value of zero, following the horizontal asymptote y = 0.

  • What is the domain and range of the arc sine function?

    -The domain of the arc sine function is from -1 to 1, and the range is from -pi/2 to pi/2.

  • What is the value of the arc sine of 1/2?

    -The value of the arc sine of 1/2 is pi/6.

  • Why is it important to consider the domain and range when evaluating the arc sine of a given value?

    -It is important to consider the domain and range because the arc sine function is only defined within those specific intervals, and values outside of these intervals do not have a corresponding arc sine value.

  • How can the limit of a rational function involving inverse trigonometric functions be evaluated as x approaches infinity?

    -The limit can be evaluated by multiplying the numerator and denominator by 1/x^3 and then determining the limit of the resulting expression, considering that terms involving 1/x^3 will approach zero.

Outlines
00:00
๐Ÿ“š Understanding Limits of Inverse Trigonometric Functions

This paragraph introduces the concept of evaluating limits of inverse trigonometric functions, specifically focusing on the inverse tangent function. It explains the graphical representation of the arc tangent function, highlighting its two horizontal asymptotes at y = pi/2 and y = -pi/2. The discussion includes how the value of the function approaches pi/2 as x approaches positive infinity and -pi/2 as x approaches negative infinity. The paragraph emphasizes the importance of understanding the graph of a function when evaluating its limits and provides a method for finding the limit of the arc tangent function as x approaches a specific value, demonstrating the process with an example.

05:01
๐Ÿ”ข Analyzing Limits with One-Sided Approaches

This paragraph delves into the technique of evaluating limits using one-sided approaches, especially when direct substitution is not possible. The example given involves the limit of arc tangent of (x - 2)/(x - 2) as x approaches 2. The explanation shows how to break down the problem into left-sided and right-sided limits, highlighting the behavior of the function as it approaches the vertical asymptote at x = 2 from both directions. The paragraph also discusses the concept of vertical and horizontal asymptotes and how they can be used to determine the behavior of the function near the point of interest. The conclusion is that the original limit does not exist due to the discrepancy between the left and right-sided limits.

10:02
๐ŸŒ Evaluating Limits of Arc Cosine and Arc Sine Functions

This paragraph explores the limits of arc cosine and arc sine functions as x approaches infinity. It begins with the graph of 1/x and its behavior near the vertical asymptote at x = 0, explaining that the limit of this expression as x approaches infinity is zero, which corresponds to the arc cosine of zero, evaluated as pi/2. The paragraph then moves on to discuss the arc sine function, detailing its domain and range, and how to find the arc sine of specific values. An example is provided, calculating the limit of a more complex expression involving arc sine as x approaches positive infinity. The explanation includes a step-by-step breakdown of the process, leading to the conclusion that the limit is pi/6. The paragraph emphasizes the importance of understanding the domain and range of trigonometric functions when solving these types of problems.

Mindmap
Keywords
๐Ÿ’กlimit
In the context of the video, a limit refers to the value that a function approaches as the input (x) gets arbitrarily large or approaches a certain point. It is a fundamental concept in calculus for understanding the behavior of functions, especially at infinity or when approaching undefined points. For instance, the video discusses the limit as x approaches infinity of the arc tangent of x, which is equal to pi/2, illustrating how the graph of the function behaves as x becomes very large.
๐Ÿ’กinverse trigonometric functions
Inverse trigonometric functions, such as the inverse tangent (arctangent) or inverse cosine (arc cosine), are mathematical functions that reverse the process of the original trigonometric functions. They are used to find the angle when the value of the trigonometric function is known. In the video, the graph of the inverse tangent function is described, with its behavior around the horizontal asymptotes y = pi/2 and y = -pi/2, which are crucial for understanding the limits as x approaches infinity or negative infinity.
๐Ÿ’กhorizontal asymptotes
A horizontal asymptote is a horizontal line that a graph of a function approaches as the input (x) becomes very large or very small. It represents the limit of the function's y-values. In the video, the graph of the inverse tangent function has two horizontal asymptotes, y = pi/2 and y = -pi/2, which provide insight into the behavior of the function at extreme values of x and are essential for evaluating limits.
๐Ÿ’กarctangent
The arctangent, or inverse tangent function, is the inverse of the tangent function and is used to find the angle whose tangent is a given value. It is one of the primary inverse trigonometric functions discussed in the video, where the behavior of the arctangent graph and its limits as x approaches infinity or negative infinity are explained in detail.
๐Ÿ’กone-sided limits
One-sided limits refer to the value that a function approaches as the input (x) gets close to a certain point from either the left or the right side. The video highlights the importance of considering one-sided limits when the function is not defined at a point, such as when evaluating the limit as x approaches 2 for the function arc tangent of (1/x - 2).
๐Ÿ’กrational function
A rational function is a function that can be expressed as the quotient of two polynomial functions. In the video, the behavior of a rational function at infinity is discussed, explaining how the degree of the denominator relative to the numerator determines the presence of horizontal asymptotes. The rational function 1/x has a horizontal asymptote at y=0 as x approaches infinity because the degree of the numerator (0) is less than the degree of the denominator (1).
๐Ÿ’กarc cosine
The arc cosine function, also known as the inverse cosine, is used to find the angle whose cosine is a given value. It is another inverse trigonometric function discussed in the video, where the limit as x approaches 2 of arc cosine of (1/x) is evaluated by considering the behavior of the cosine function and its inverse.
๐Ÿ’กvertical asymptote
A vertical asymptote is a vertical line that the graph of a function approaches but never reaches as the input (x) gets close to a certain value. In the video, the vertical asymptote at x=0 for the function 1/x is mentioned, which is a key feature in understanding the behavior of the function near the asymptote and in evaluating limits.
๐Ÿ’กdomain and range
The domain of a function is the set of all possible input values (x-values), and the range is the set of all possible output values (y-values). In the context of the video, understanding the domain and range of inverse trigonometric functions like arc sine is crucial for determining the limits and the behavior of these functions. For example, the domain of arc sine is from -1 to 1, and the range is from -pi/2 to pi/2.
๐Ÿ’กarc sine
The arc sine function, or inverse sine, is used to find the angle whose sine is a given value. It is an inverse trigonometric function with a domain from -1 to 1 and a range from -pi/2 to pi/2. In the video, the arc sine function is used to evaluate the limit as x approaches infinity of the expression (arc sine of 5 + 2x^3/4) / (x^3 - 8), which simplifies to pi/6 due to the behavior of the function at infinity.
๐Ÿ’กsine function
The sine function is a fundamental trigonometric function that relates the angle of a right triangle to the ratio of the length of the side opposite the angle to the length of the hypotenuse. In the video, the sine function is discussed in relation to the arc sine function, where the sine of pi/6 is equal to 1/2, which is used to determine the value of the limit in the given example.
Highlights

The limit of the inverse tangent of x as x approaches infinity is pi/2.

The graph of the inverse tangent function has two horizontal asymptotes at y = pi/2 and y = -pi/2.

The limit of the inverse tangent of x as x approaches negative infinity is -pi/2.

Evaluating limits of inverse trigonometric functions is simplified by understanding their graphs.

The limit of arc tangent of (1/x - 2) as x approaches 2 does not exist due to differing left and right sided limits.

The limit of arc tangent from the left side as x approaches 2 is negative infinity.

The limit of arc tangent from the right side as x approaches 2 is positive infinity.

The graph of 1/x has a vertical asymptote at x=0 and a horizontal asymptote of y=0.

The limit as x approaches infinity for the expression 1/x is 0, which is equal to the arc cosine of zero.

Arc cosine of zero is pi/2, as cosine of pi/2 is 0.

The limit as x approaches infinity for the expression arcsin(5 + 2x^3)/(x^3 - 8) is pi/6.

The domain of arcsine is -1 to 1, and the range is -pi/2 to pi/2.

Sine of pi/6 is 1/2, thus the arc sine of 1/2 is pi/6.

When dealing with limits at infinity, rational functions can be manipulated by multiplying the numerator and denominator by 1/x^3.

The arc sine function only exists in quadrants III and IV of the unit circle.

Sine of 5pi/6 is 1/2, but arc sine of 1/2 does not equal 5pi/6 due to the limited range of arc sine.

This video provides a comprehensive guide on solving limits involving inverse trigonometric functions.

Transcripts

Browse More Related Video

Math 133 Lecture 2 6

Limits "at" infinity

AP Calculus AB - 1.15 Connecting Limits at Infinity and Horizontal Asymptotes

Introduction to infinite limits | Limits and continuity | AP Calculus AB | Khan Academy

Finding limits at infinity using squeeze theorem | Squeeze or Sandwich Theorem - Calculus

Limits at Infinity & Horizontal Asymptotes

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Inverse TrigonometryLimits CalculationAsymptotesGraph AnalysisTrigonometric FunctionsMathematics TutorialEducational ContentAdvanced MathOnline LearningInverse Tangent