Which are the Three Functions in Trigonometry? | Don't Memorise

Infinity Learn NEET
19 Dec 201405:21
EducationalLearning
32 Likes 10 Comments

TLDRThis educational video script introduces the three fundamental trigonometric functions—sine, cosine, and tangent—using a right triangle. It explains that sine (sin) is the ratio of the opposite side to the hypotenuse, cosine (cos) is the ratio of the adjacent side to the hypotenuse, and tangent (tan) is the ratio of the opposite side to the adjacent side. The script also demonstrates a key trigonometric identity, sin(θ)/cos(θ) = tan(θ), and offers a mnemonic 'SOA' to remember the formulas. It concludes with an example using a triangle with sides of 3, 4, and 5 units to calculate these functions, emphasizing the practical application of trigonometry.

Takeaways
  • 📚 The script introduces the three fundamental trigonometric functions: sine (sin), cosine (cos), and tangent (tan), all based on a right-angled triangle.
  • 📐 The sine function is defined as the ratio of the length of the side opposite to the angle (Theta) to the length of the hypotenuse.
  • 📏 Cosine is the ratio of the length of the side adjacent to the angle (Theta) to the length of the hypotenuse.
  • 🔄 The tangent function is the ratio of the length of the side opposite to the angle (Theta) to the length of the side adjacent to the angle.
  • 🔄 The term 'tangent' is derived from the geometric concept where a line touches the circle at exactly one point, but the script clarifies that the circle is not directly involved in the trigonometric function.
  • 🧩 The script demonstrates a key trigonometric identity: sin(Theta) / cos(Theta) equals tan(Theta), showing how these functions are interrelated.
  • 🔢 To illustrate the functions, the script provides an example using a right triangle with sides of lengths 3, 4, and 5 units, where 5 is the hypotenuse.
  • 📉 The script shows the calculation of sin(Theta), cos(Theta), and tan(Theta) for the given triangle, using the lengths of the sides.
  • 📝 The script suggests a mnemonic device, 'SOA', to remember the order of the trigonometric functions: sine (S), cosine (O), and tangent (A).
  • 🔑 The script emphasizes the importance of understanding how these trigonometric functions vary with angles and suggests watching another video for a deeper understanding.
  • 🎶 The script ends with a reference to music, indicating that it is part of a video with an accompanying soundtrack.
Q & A

  • What are the three primary trigonometric functions discussed in the script?

    -The three primary trigonometric functions discussed in the script are sine (sin), cosine (cos), and tangent (tan).

  • How is the sine function of an angle Theta defined in the context of a right triangle?

    -The sine function of an angle Theta, denoted as sin Theta, is defined as the ratio of the length of the side opposite to Theta to the length of the hypotenuse.

  • What does the cosine function represent in a right triangle?

    -The cosine function, represented as cos Theta, is the ratio of the length of the side adjacent to Theta to the length of the hypotenuse.

  • Can you explain the definition of the tangent function in the script?

    -The tangent function, denoted as tan Theta, is the ratio of the length of the side opposite to Theta to the length of the side adjacent to Theta.

  • What is the relationship between sin Theta and cos Theta when you divide them?

    -When you divide sin Theta by cos Theta, the result is equal to tan Theta, which is the tangent of the angle.

  • How can the reciprocal of cos Theta be expressed in terms of the sides of a right triangle?

    -The reciprocal of cos Theta can be expressed as the hypotenuse divided by the adjacent side.

  • What mnemonic is provided in the script to help remember the trigonometric functions' formulas?

    -The mnemonic provided in the script is 'SOA', which stands for Sine Opposite by Hypotenuse, Cosine Adjacent by Hypotenuse, and Tangent Opposite by Adjacent.

  • In the script, how is the value of sin Theta calculated for a right triangle with sides of length 3, 4, and 5 units?

    -For a right triangle with sides of length 3 (opposite) and 5 (hypotenuse), the value of sin Theta is calculated as 3 divided by 5.

  • What is the approximate value of cos Theta for the same triangle mentioned in the previous question?

    -For the same triangle with a side of length 4 (adjacent) and a hypotenuse of length 5, the value of cos Theta is approximately 0.8.

  • How is tan Theta calculated for the triangle with sides of length 3 and 4 units?

    -Tan Theta is calculated by dividing the length of the opposite side (3 units) by the length of the adjacent side (4 units), resulting in a value of 3/4 or 0.75.

  • What does the script suggest for understanding how trigonometric functions vary with angles?

    -The script suggests watching another video that is based on unit circles to understand how the trigonometric functions vary with angles.

Outlines
00:00
📚 Introduction to Trigonometry Functions

This paragraph introduces the fundamental trigonometric functions within the context of a right-angled triangle. It explains the sine (sin), cosine (cos), and tangent (tan) functions, defining them as ratios of the lengths of the sides relative to an angle, Theta. The paragraph also demonstrates a key trigonometric identity, sin(Theta)/cos(Theta) = tan(Theta), by simplifying the expression and highlighting the reciprocal relationship between the sine and cosine functions. A mnemonic, 'SOA', is introduced to help remember the formulas: sin Theta is 'opposite by hypotenuse', cos Theta is 'adjacent by hypotenuse', and tan Theta is 'opposite by adjacent'. The paragraph concludes with an example using a triangle with sides of lengths 3, 4, and 5 units to calculate the values of these trigonometric functions.

05:01
🎥 Further Exploration of Trigonometric Functions

The second paragraph serves as a transition, encouraging viewers to watch additional videos for a deeper understanding of how trigonometric functions vary with different angles. It mentions the importance of the unit circle in the study of trigonometry, hinting at more advanced concepts that will be covered in subsequent educational content. The paragraph is concluded with background music, creating an engaging and inviting tone for the audience to continue their learning journey.

Mindmap
Keywords
💡Trigonometry
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles, particularly right-angled triangles. In the video script, trigonometry is the main theme, as the presenter discusses the fundamental trigonometric functions in the context of a right-angled triangle. The script uses trigonometry to explain the sine, cosine, and tangent functions, which are essential for understanding the relationships between the angles and sides of a triangle.
💡Theta (θ)
Theta, often represented by the symbol θ, is the Greek letter used in trigonometry to denote an angle within a triangle. In the script, theta is the angle of interest in a right-angled triangle, and the trigonometric functions are defined in relation to this angle. The sine, cosine, and tangent are all ratios that involve theta and are used to find unknown sides or angles in a triangle.
💡Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, which is opposite the right angle. In the script, the hypotenuse is used as the denominator in the definitions of sine and cosine functions. It is a critical component in trigonometric calculations and is the reference for the other two sides in the triangle.
💡Adjacent Side
Adjacent side refers to the side of a right-angled triangle that is next to the angle being considered but not the hypotenuse. In the script, the adjacent side is used in the definition of the cosine function, where it is the numerator in the ratio that defines cosine as 'adjacent by hypotenuse'.
💡Opposite Side
The opposite side is the side of a right-angled triangle that is across from the angle being considered. In the script, the opposite side is used in the definition of the sine function, where it is the numerator in the ratio that defines sine as 'opposite by hypotenuse'.
💡Sine Function (sin)
The sine function, represented as sin, is one of the primary trigonometric functions. It is defined as the ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle. In the script, the presenter explains that sin θ equals 'opposite by hypotenuse' and provides an example with a triangle where the opposite side is 3 units and the hypotenuse is 5 units.
💡Cosine Function (cos)
The cosine function, denoted as cos, is another fundamental trigonometric function. It is the ratio of the length of the adjacent side to the length of the hypotenuse. The script illustrates this by stating that cos θ equals 'adjacent by hypotenuse', and an example is given with an adjacent side of 4 units and a hypotenuse of 5 units, resulting in a cosine value of approximately 0.8.
💡Tangent Function (tan)
The tangent function, symbolized as tan, is the ratio of the length of the opposite side to the length of the adjacent side in a right-angled triangle. The script explains that tan θ equals 'opposite by adjacent'. It is also highlighted that the tangent function can be derived from the sine and cosine functions, as tan θ is sin θ divided by cos θ.
💡Reciprocal
A reciprocal is a number which, when multiplied by the original number, results in a product of one. In the context of the script, the reciprocal of the cosine function is used to derive the sine function divided by the cosine function, which simplifies to the tangent function. This is an important concept in understanding the relationship between the trigonometric functions.
💡SOHCAHTOA
SOHCAHTOA is a mnemonic used to remember the definitions of the trigonometric functions sine, cosine, and tangent. In the script, it is introduced as a way to remember that 'sin theta equals opposite by hypotenuse', 'cos theta equals adjacent by hypotenuse', and 'tan theta equals opposite by adjacent'. The acronym is derived from the first letters of each part of the definitions and is a common tool for students learning trigonometry.
💡Right-Angled Triangle
A right-angled triangle is a triangle that has one angle that is exactly 90 degrees. In the script, the right-angled triangle is the basis for explaining the trigonometric functions sine, cosine, and tangent. The triangle with sides of lengths 3, 4, and 5 units is used as an example to demonstrate how to calculate these trigonometric ratios.
Highlights

Introduction to the three fundamental trigonometric functions using a right triangle.

Definition of sine function as sin(θ) = opposite/hypotenuse.

Explanation of cosine function as cos(θ) = adjacent/hypotenuse.

Description of tangent function as tan(θ) = opposite/adjacent.

Clarification on the absence of the word 'ine' in the cosine function.

Mnemonic 'SOA' to remember the trigonometric functions: Sine, Opposite, Hypotenuse; Cosine, Adjacent, Hypotenuse; Tangent, Opposite, Adjacent.

Demonstration of the trigonometric identity sin(θ)/cos(θ) = tan(θ).

Explanation of how to derive the tangent function from the sine and cosine functions.

Illustration of the reciprocal relationship between cosine and tangent functions.

Cancellation of the hypotenuse in the derivation of the tangent function.

Introduction of a right triangle with sides 3, 4, and 5 units to demonstrate the application of trigonometric functions.

Calculation of sin(θ) using the side opposite to θ and the hypotenuse.

Calculation of cos(θ) using the side adjacent to θ and the hypotenuse, resulting in approximately 0.8.

Calculation of tan(θ) using the side opposite to θ and the side adjacent to θ.

Emphasis on the importance of understanding how trigonometric functions vary with angles.

Encouragement to watch additional videos for a deeper understanding of trigonometric functions.

End of the video with a reminder of the core concepts covered.

Transcripts

Browse More Related Video

Trig - 0.6 Trig Functions of Acute Angles

When Do I use Sin, Cos or Tan?

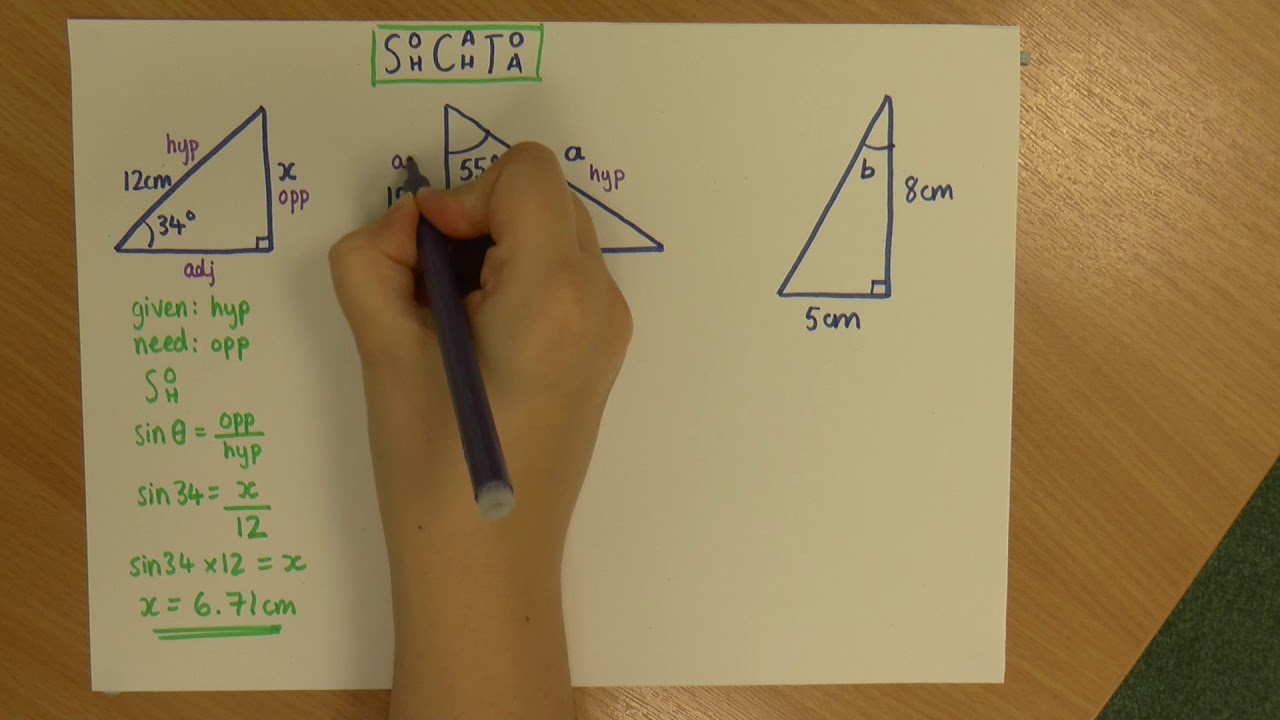
Trigonometry: Finding missing sides and angles

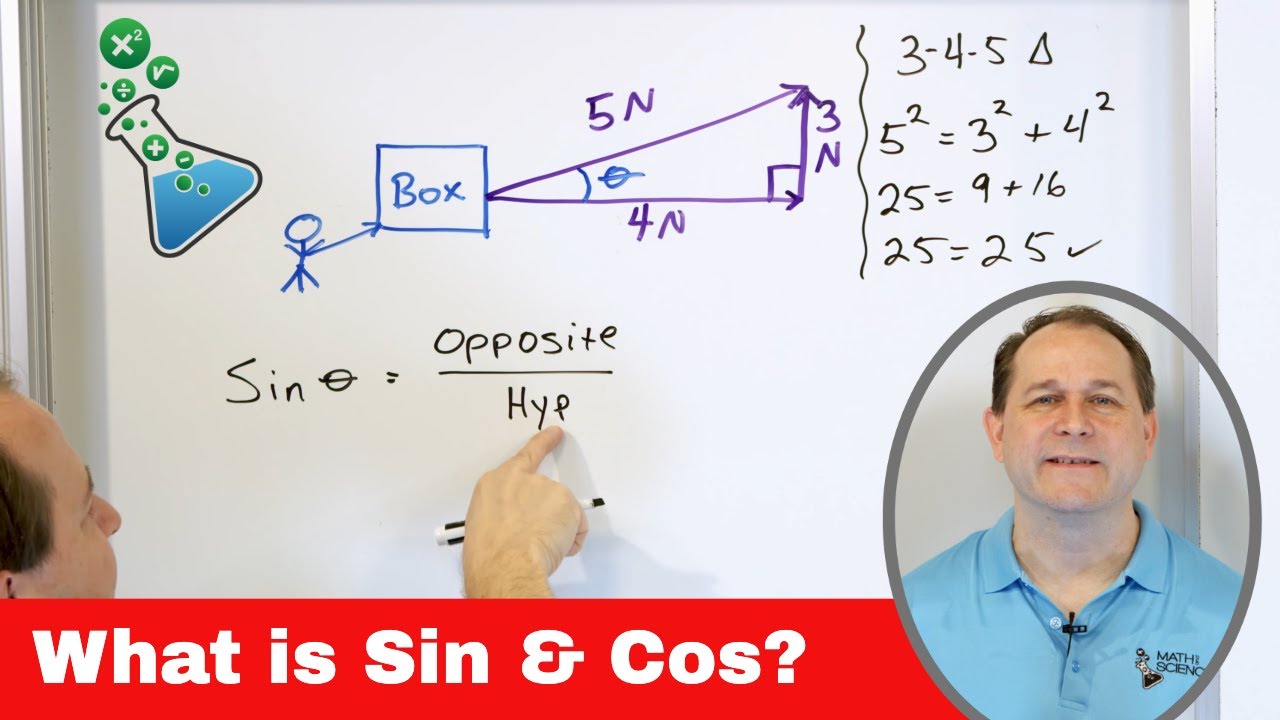
05 - Sine and Cosine - Definition & Meaning - Part 1 - What is Sin(x) & Cos(x) ?

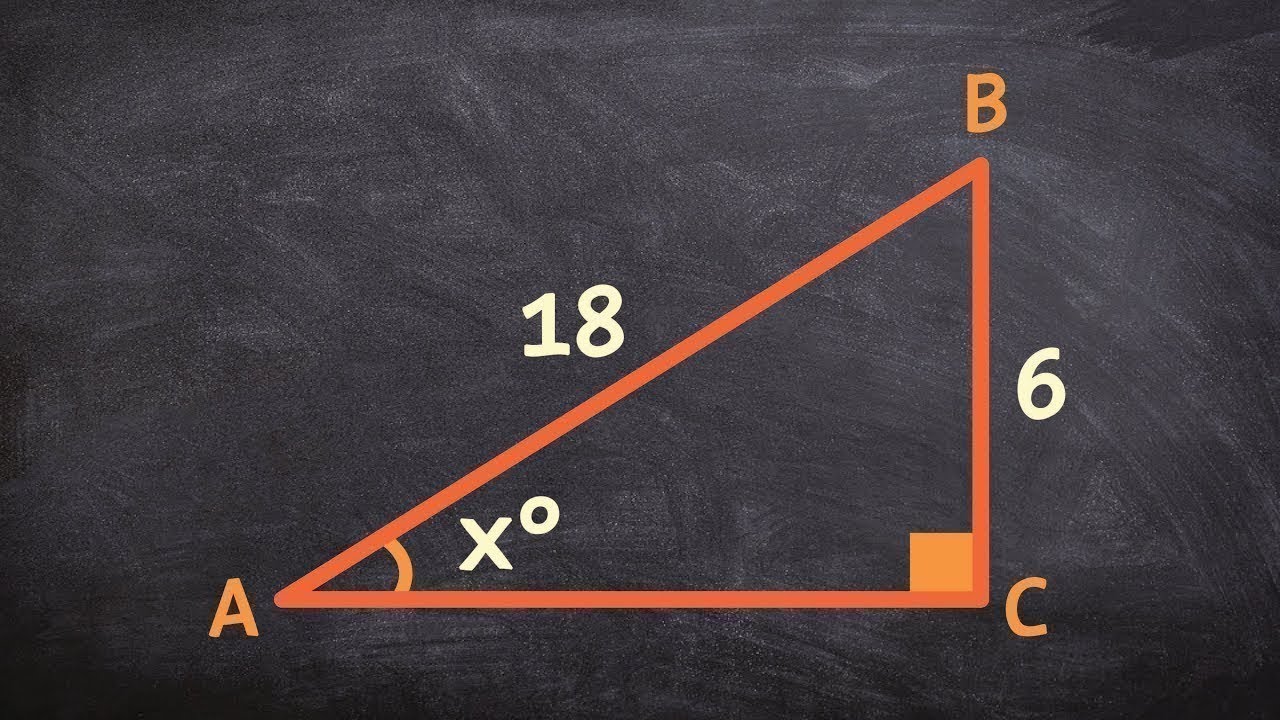
Learn to find the missing angles for a triangle using inverse trig functions

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Trigonometry BasicsRight TriangleSine FunctionCosine FunctionTangent FunctionMath EducationFormula MemorizationSOH-CAH-TOARatios in TrianglesTrigonometric RatiosGeometry Tutorial