Basic Trigonometry: Sin Cos Tan (NancyPi)
TLDRIn this educational video, Nancy introduces the basics of trigonometric functions, focusing on sine, cosine, and tangent, using the mnemonic SOH-CAH-TOA. She explains the roles of the hypotenuse, adjacent, and opposite sides in relation to a given angle, theta, in right triangles. Nancy demonstrates how to calculate these functions with a sample triangle, and extends the discussion to cosecant, secant, and cotangent by finding their values through the reciprocals of sine, cosine, and tangent, respectively. She also addresses common confusions related to triangle orientation and emphasizes the importance of correctly writing trigonometric expressions.
Takeaways
- 📐 **Basic Trigonometric Functions**: The video introduces sine (sin), cosine (cos), and tangent (tan) as the primary trigonometric functions.
- 🔢 **Memory Trick**: SOH-CAH-TOA is a mnemonic to remember the relationships between sides of a right triangle and the trigonometric functions.
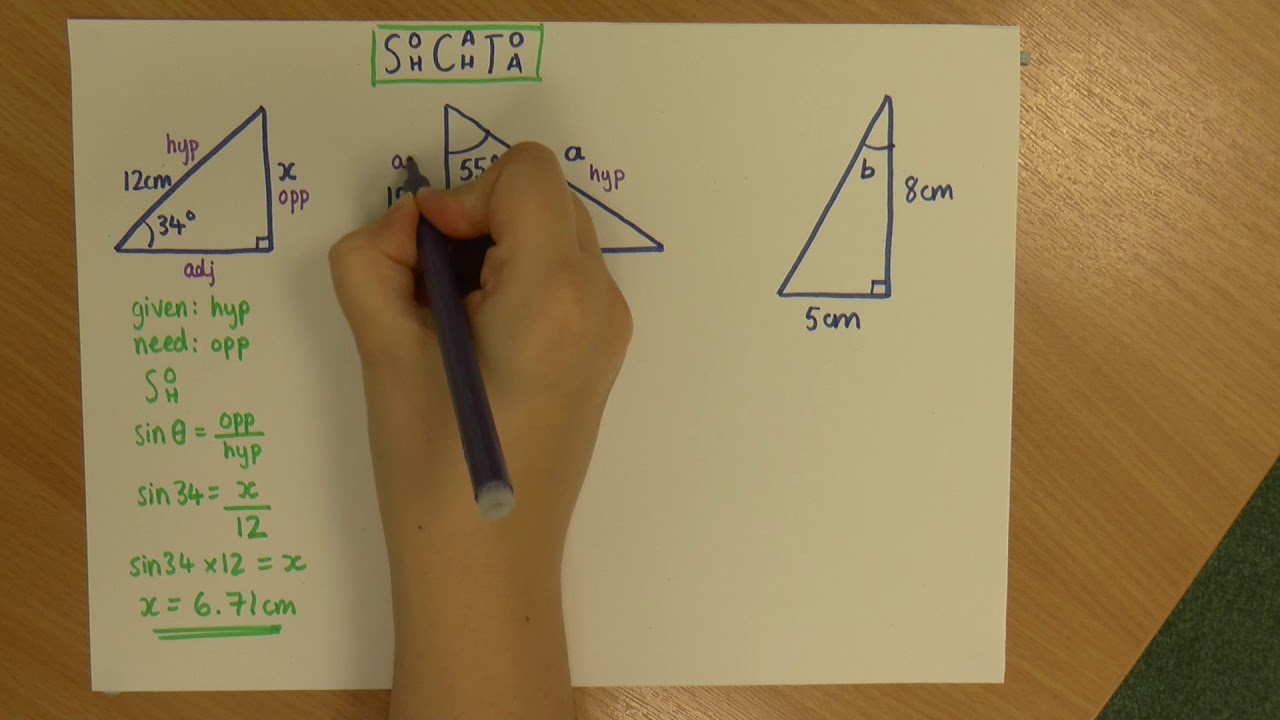
- 📐 **Right Triangles**: All six trigonometric functions are based on right triangles, which have a 90-degree angle.
- 📏 **Sides of a Triangle**: The sides in relation to an angle (theta) are the hypotenuse (longest side), adjacent (next to theta, not the hypotenuse), and opposite (directly opposite theta).
- 🔑 **Defining sin, cos, and tan**: sin is opposite/hypotenuse, cos is adjacent/hypotenuse, and tan is opposite/adjacent.
- 💡 **Finding Trigonometric Values**: Given a right triangle with side lengths, one can calculate sin, cos, and tan of theta using the SOH-CAH-TOA mnemonic.
- 🔄 **Reciprocal Functions**: The reciprocal of sin, cos, and tan gives csc (cosecant), sec (secant), and cot (cotangent) respectively.
- 🔀 **Orientation of Triangles**: Regardless of the orientation of the right triangle, the hypotenuse remains the longest side, and the sides are still classified as opposite, adjacent, and hypotenuse based on their relation to theta.
- 📝 **Writing Final Answers**: When providing the value of a trigonometric function, it is important to include the angle (theta) to give context to the value.
- 📈 **Understanding and Applying**: The video emphasizes the importance of understanding the underlying concepts and applying them correctly to solve trigonometric problems.
- 🌐 **Misconceptions**: Common confusion arises when the right triangle is drawn in different orientations, but the principles remain the same.
- 🎓 **Complete Expressions**: It's crucial to write the full expression of the trigonometric function with the angle (e.g., sin(theta)) to convey the correct meaning.
Q & A
What is the purpose of the mnemonic SOH-CAH-TOA in trigonometry?
-SOH-CAH-TOA is a mnemonic device used to help remember the definitions of the sine, cosine, and tangent functions in trigonometry. 'SOH' stands for Sine equals Opposite over Hypotenuse, 'CAH' for Cosine equals Adjacent over Hypotenuse, and 'TOA' for Tangent equals Opposite over Adjacent.
How are the sides of a right triangle defined in relation to a specific angle?
-In a right triangle, the side opposite the right angle is called the hypotenuse. The side next to the angle of interest, but not the hypotenuse, is called the adjacent side. The side opposite the angle of interest is known as the opposite side.
What are the reciprocal trigonometric functions mentioned in the transcript?
-The reciprocal trigonometric functions mentioned are cosecant (csc), secant (sec), and cotangent (cot). Cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent.
How can you calculate the cosecant of an angle using the sine function?
-To calculate the cosecant of an angle, first find the sine of the angle. Cosecant is the reciprocal of sine. So, if sine of an angle is a/b, then cosecant of the angle will be b/a.
What should be included in the final answer when solving for trigonometric functions?
-When writing the final answer for trigonometric functions, it is important to include the angle. For example, rather than writing 'sin = 3/5', it should be written as 'sin(theta) = 3/5'. This specifies the angle for which the sine value is calculated, providing clarity.
What common mistakes do people make when triangles are oriented differently?
-Common mistakes occur when the orientation of the triangle changes (e.g., upside down or horizontal). People often mislabel the sides relative to the angle of interest. Understanding that the names of the sides (opposite, adjacent, hypotenuse) are relative to the angle being referenced helps avoid these errors.
How do you determine the tangent of an angle from a right triangle?
-To determine the tangent of an angle in a right triangle, use the opposite side length divided by the adjacent side length. This follows from the 'TOA' part of the SOH-CAH-TOA mnemonic.
What is the correct process to find the secant of an angle?
-To find the secant of an angle, first calculate the cosine of that angle. Then, take the reciprocal of the cosine value. For example, if the cosine of theta is 3/5, the secant of theta will be 5/3.
Why is it important to correctly label the sides of the triangle in relation to the angle theta?
-Correctly labeling the sides of the triangle in relation to theta is crucial because the definitions of sine, cosine, and tangent depend on the relative positions of the sides. Mislabeling can lead to incorrect calculations and results.
How do trigonometric functions help in understanding right triangles?
-Trigonometric functions provide a mathematical method to relate the angles of a triangle to its side lengths. This is particularly useful in solving problems involving right triangles, where these functions help in calculating unknown angles or sides based on known values.
Outlines
📐 Introduction to Basic Trigonometry Functions
Nancy introduces the basic trigonometric functions: sine, cosine, and tangent, along with their reciprocals: cosecant, secant, and cotangent. She explains the mnemonic 'SOH-CAH-TOA' to remember how these functions are calculated using the sides of a right triangle. Nancy details the roles of the hypotenuse, adjacent, and opposite sides relative to a given angle, theta. Using a right triangle with sides of lengths 3, 4, and 5, she demonstrates how to find the values of sine, cosine, and tangent for theta.
🔍 Calculating Reciprocal Trigonometry Functions
Nancy explores how to find the values of the cosecant, secant, and cotangent functions by first calculating their corresponding primary trigonometric functions. Using a right triangle from the previous example, she calculates sine, cosine, and tangent of theta, and then finds their reciprocals to determine cosecant, secant, and cotangent. Nancy also discusses common mistakes, such as misidentifying sides based on the triangle's orientation, and provides visual examples of right triangles in various orientations to clarify where the hypotenuse, opposite, and adjacent sides are.
🧐 Importance of Labeling in Trigonometry
In the final segment, Nancy emphasizes the importance of correctly labeling the trigonometric functions with the angle theta to avoid confusion. She revisits the triangle orientations and labels the sides in each scenario to show how the definitions of hypotenuse, opposite, and adjacent change based on theta's position. Nancy wraps up by encouraging viewers to appreciate trigonometry despite its complexities and invites them to like and subscribe if they found the video helpful.
Mindmap
Keywords
💡Trigonometric functions
💡SOH-CAH-TOA
💡Right triangle
💡Hypotenuse
💡Adjacent side
💡Opposite side
💡Cosecant (csc)
💡Secant (sec)
💡Cotangent (cot)
💡Reciprocal
💡Angle notation
Highlights
Nancy introduces the six basic trigonometric functions: sine, cosine, tangent, cosecant, secant, and cotangent.
The memory trick SOH-CAH-TOA is explained to help remember the meaning of sin, cos, and tan.
All trigonometric functions involve right triangles, with the right angle noted by a corner symbol.
Theta is identified as the angle in a right triangle that is not the right angle.
The hypotenuse is the longest side of the triangle and is opposite the right angle.
The adjacent side is the side next to theta that is not the hypotenuse.
The opposite side is the third side of the triangle, directly opposite theta.
sin(theta) is calculated as the ratio of the opposite side to the hypotenuse (SOH).
cos(theta) is calculated as the ratio of the adjacent side to the hypotenuse (CAH).
tan(theta) is calculated as the ratio of the opposite side to the adjacent side (TOA).
Cosecant, secant, and cotangent are found by taking the reciprocal of their respective trigonometric functions.
csc(theta) is found by flipping the numerator and denominator of sin(theta).
sec(theta) is found by flipping the numerator and denominator of cos(theta).
cot(theta) is found by taking the reciprocal of tan(theta).
Different orientations of the right triangle can confuse the identification of sides, but the hypotenuse remains the longest side.
Regardless of orientation, the side next to theta is the adjacent side, and the one opposite theta is the opposite side.
When writing the final answer, it's important to include the angle (theta) to give context to the trigonometric value.
Nancy emphasizes the importance of writing the full answer with the angle to ensure meaning and clarity.
The video aims to make understanding trigonometric functions accessible and engaging for the audience.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: