When Do I use Sin, Cos or Tan?
TLDRThe video script is an informative guide on understanding when to use cosine, sine, or tangent in trigonometry. It explains the basics of right triangles, including the definitions of hypotenuse, opposite, and adjacent sides, and how these relate to the trigonometric functions. The video uses a 30-60-90 triangle to illustrate the concepts and provides examples of how to apply the functions to find missing angles or sides. It also introduces memory aids like 'Soho cahoots and toads' to help remember the functions: sine is opposite/hypotenuse, cosine is adjacent/hypotenuse, and tangent is opposite/adjacent. The script emphasizes the importance of understanding these relationships for solving problems in trigonometry.
Takeaways
- 📐 Understanding the context: The video explains when to use cosine, sine, or tangent in the context of right triangles, focusing on their applications rather than their computation.
- 🔢 Trigonometric functions: Trigonometric functions (sine, cosine, tangent) help in calculating unknown sides and angles in right triangles when given two pieces of information.
- ✅ Right triangle properties: A right triangle has 90 degrees and two acute angles that sum up to 90 degrees, with the hypotenuse being the longest side opposite the right angle.
- 📌 Triangle terminology: The sides adjacent to the right angle are called legs, and the longest side is the hypotenuse. The side opposite a given angle is referred to as the opposite side.
- 📈 Ratios in 30-60-90 triangles: In a 30-60-90 triangle, the ratio of the side lengths is consistent, with the side opposite the 30-degree angle being half the length of the hypotenuse.
- 🔍 Sine function: Sine (sin) is defined as the ratio of the length of the opposite side to the length of the hypotenuse.
- 🌐 Cosine function: Cosine (cos) is defined as the ratio of the length of the adjacent side to the length of the hypotenuse.
- 📐 Tangent function: Tangent (tan) is defined as the ratio of the length of the opposite side to the length of the adjacent side.
- 🤔 Problem-solving strategy: To solve for missing sides or angles, one must identify which trigonometric function corresponds to the known and unknown values.
- 💡 Memory aids: The video suggests using mnemonic devices like 'Soho cahoots and toads' or the traditional 'sohcahtoa' to remember the trigonometric functions: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent).
Q & A
What is the main focus of the video?
-The main focus of the video is to explain when to use cosine, sine, or tangent in the context of right triangles, rather than how to use them.
How many sides and angles are there in a right triangle?
-A right triangle has three sides, with one being the hypotenuse, and two angles, both of which are acute and add up to 90 degrees.
What does the 'D' notation in a right triangle signify?
-The 'D' notation signifies that the triangle contains a right angle, which is 90 degrees or a quarter of a circle.
What is the significance of knowing two things about a right triangle?
-If you know two things about a right triangle, such as the lengths of two sides or the measure of an angle, you can calculate all the other sides, angles, area, and perimeter.
What are the names of the sides in a right triangle relative to an angle θ?
-The side opposite to angle θ is called the opposite side, the side next to angle θ is called the adjacent side, and the longest side opposite the right angle is the hypotenuse.
What is the sine of 30 degrees in a 30-60-90 triangle?
-In a 30-60-90 triangle, the sine of 30 degrees is a pure number equal to 1/2, representing the ratio of the length of the opposite side to the hypotenuse.
How does the video suggest remembering the trigonometric functions?
-The video suggests using a memory device such as associating the first letters of sine, cosine, and tangent with the words 'Soho', 'cahoots', and 'toads' to remember their respective functions.
What is the tangent function in terms of sides and angles in a right triangle?
-The tangent function is the ratio of the length of the opposite side to the length of the adjacent side, represented as tan(θ) = opposite/adjacent.
How can you find the hypotenuse if you know the angle and the length of the opposite side?
-If you know the angle and the length of the opposite side, you can use the sine function to find the hypotenuse. The sine of the angle is equal to the opposite side length divided by the hypotenuse, allowing you to solve for the hypotenuse length.
What is the cosine function used for in a right triangle?
-The cosine function is used to find the length of the adjacent side when you know the angle and the length of the hypotenuse. It is represented as cos(θ) = adjacent/hypotenuse.
How can you determine if your answer in trigonometry makes sense?
-To determine if your answer makes sense, you should check if it aligns with the properties of a right triangle, such as the hypotenuse being the longest side and if the calculated angles sum up to 90 degrees.
Outlines
📚 Introduction to Trigonometry
This paragraph introduces the basics of trigonometry, focusing on the right triangle and its relationship with sine, cosine, and tangent. It emphasizes the importance of understanding when to use each function rather than their application. The concept of right triangles having 90 degrees and two acute angles that sum up to 90 degrees is explained. The paragraph also introduces the notation for right angles and unknown angles (denoted by theta). It explains the terms hypotenuse, opposite, and adjacent sides in the context of right triangles.
📐 Understanding Trigonometric Ratios
The paragraph delves into the concept of trigonometric ratios, specifically sine, cosine, and tangent, in the context of a 30-60-90 triangle. It explains how knowing the length of any two sides allows for the calculation of the third side and the angles. The ratios are described as pure numbers, with examples given for sine, cosine, and tangent at a 30-degree angle. The paragraph also discusses how these ratios can be used to find missing sides or angles in right triangles, given certain information.
🔢 Trigonometric Functions and Their Applications
This section further explores the application of trigonometric functions when the angle or sides are known. It explains how to use sine, cosine, and tangent to find missing lengths or angles in a right triangle. The paragraph uses examples to illustrate how these functions work, emphasizing the importance of understanding the relationships between sides and angles. It also touches on the concept of pure numbers in trigonometry and how they can be found using a calculator or charts.
📊 Using Charts and Algebra for Trigonometric Problems
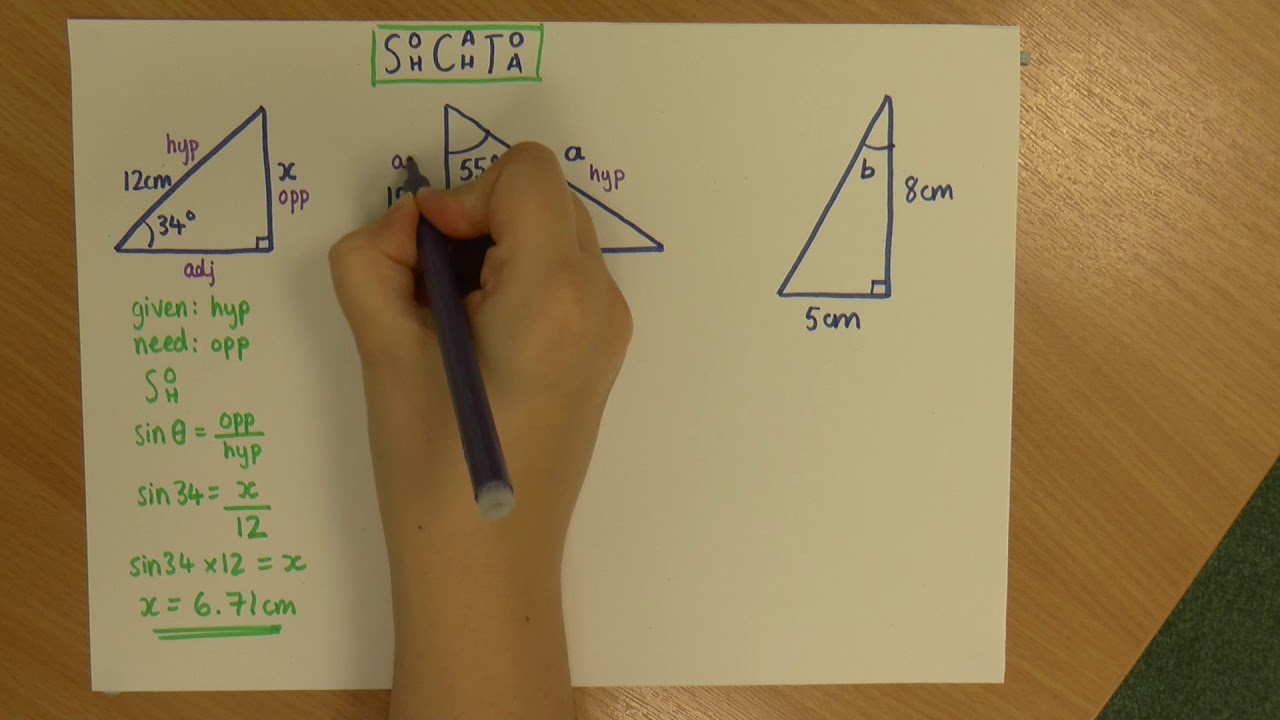
The paragraph discusses the use of charts and algebraic methods to solve trigonometric problems. It explains how to find the hypotenuse or other sides of a right triangle when given an angle and the length of one side, using sine, cosine, or tangent. The process involves looking up values in charts or using a calculator and then applying algebra to find the unknowns. The paragraph also highlights the importance of checking the logic of the answer against the properties of right triangles.
🧠 Mnemonics for Remembering Trigonometric Functions
In this paragraph, the speaker shares a personal mnemonic device to remember the trigonometric functions: sine, cosine, and tangent. The mnemonic 'Soho cahoots and toads' is introduced to help recall that sine is the opposite side divided by the hypotenuse, cosine is the adjacent side divided by the hypotenuse, and tangent is the opposite side divided by the adjacent side. The speaker also mentions the traditional mnemonic 'sohcahtoa' and encourages the audience to find mnemonics that work best for them.
Mindmap
Keywords
💡Trigonometric Functions
💡Right Triangles
💡Hypotenuse
💡Acute Angles
💡Sine (sin)
💡Cosine (cos)
💡Tangent (tan)
💡Theta (θ)
💡Opposite Side
💡Adjacent Side
💡Memory Devices
Highlights
The video explains when to use cosine, sine, or tangent in trigonometry.
Trigonometric functions are useful for calculating unknown sides and angles in right triangles.
A right triangle can be fully calculated with two known values (two sides or one side and an angle).
The symbol 'D' denotes a right angle (90 degrees) in a triangle.
Theta (θ) represents an unknown angle in a right triangle.
The hypotenuse is the longest side and is opposite the right angle in a right triangle.
The words 'opposite' and 'adjacent' refer to the sides next to and opposite the angle in question.
The sine function is the ratio of the length of the opposite side to the hypotenuse.
The cosine function is the ratio of the length of the adjacent side to the hypotenuse.
The tangent function is the ratio of the length of the opposite side to the adjacent side.
A 30-60-90 triangle has specific ratios that remain constant for all such triangles.
The sine, cosine, and tangent values are pure numbers and can be found on charts or calculators.
The video provides a mnemonic device (Soho, cahoots, toads) to remember the trigonometric functions.
Traditional mnemonic device is 'sohcahtoa' to remember the trigonometric functions.
The video includes practice problems and links to additional resources for learning trigonometry.
The interior angles of all triangles in the universe sum up to 180 degrees.
The hypotenuse remains the same regardless of how the triangle is rotated around it.
The video emphasizes the importance of checking if the calculated answer makes sense in the context of the problem.
Transcripts
Browse More Related Video
Trigonometry: Finding missing sides and angles

Trig - 0.6 Trig Functions of Acute Angles

Which are the Three Functions in Trigonometry? | Don't Memorise

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

Finding Sides and Angles with Right Triangle Trigonometry (Precalculus - Trigonometry 31)

Trigonometry made easy
5.0 / 5 (0 votes)
Thanks for rating: