Trigonometry made easy

tecmath
16 Oct 201912:43
EducationalLearning
32 Likes 10 Comments

TLDRThe Tech Math Channel's video offers an insightful introduction to trigonometry, focusing on the study of relationships between the sides and angles of a right-angle triangle. The host explains the fundamental concepts by labeling the sides as opposite, adjacent, and hypotenuse in relation to an angle named Theta. Key trigonometric functions—sine, cosine, and tangent—are introduced as ratios of these sides. The video then demonstrates how to apply these functions to solve for unknown side lengths and angles, using examples and mnemonic devices like 'SOHCAHTOA' to aid understanding. It emphasizes the importance of using a calculator effectively to find both trigonometric values and their inverses. The presenter encourages viewers to practice these techniques and offers further assistance for any difficulties, inviting engagement with the channel.

Takeaways
  • 📐 Trigonometry is the study of the relationships between the sides and angles of a right-angle triangle.
  • 📏 The three main trigonometric functions are sine (sin), cosine (cos), and tangent (tan), which relate the sides of a triangle to its angles.
  • 🔢 To solve trigonometric problems, first label the sides of the triangle as opposite (O), adjacent (A), and hypotenuse (H).
  • 🧮 The sine function is defined as the ratio of the opposite side to the hypotenuse.
  • 📐 The cosine function is the ratio of the adjacent side to the hypotenuse.
  • 📏 The tangent function is the ratio of the opposite side to the adjacent side.
  • 📚 Memorizing the acronym SOH-CAH-TOA can help remember these relationships: Sine = Opposite/Hypotenuse, Cosine = Adjacent/Hypotenuse, Tangent = Opposite/Adjacent.
  • 🔑 To find an unknown side length, use the appropriate trigonometric function based on the given angle and known side lengths.
  • 🧵 To find an unknown angle, use the inverse trigonometric functions available on most calculators (e.g., sin^-1 for the inverse sine function).
  • 💡 When solving for an unknown side, it may be helpful to create a 'friendly' equation alongside the trigonometric equation to assist with the calculation.
  • ✅ Always ensure you know how to use the specific functions and inverse functions on your calculator to solve trigonometric problems.
  • 🌐 The video provides examples of solving for unknown side lengths and angles in right-angle triangles using trigonometry.
Q & A

  • What is trigonometry primarily concerned with?

    -Trigonometry is a branch of mathematics that studies the relationships between the angles and sides of right-angled triangles.

  • How can trigonometry be used in practical scenarios?

    -Trigonometry can be used to calculate unknown side lengths or angles in right-angled triangles, using known side lengths or angles.

  • What are the names of the sides of a right-angle triangle in trigonometry?

    -The sides of a right-angle triangle are called the hypotenuse (the longest side), the opposite (the side opposite the angle of interest), and the adjacent (the side next to the angle of interest).

  • What are the main trigonometric functions and what do they represent?

    -The main trigonometric functions are sine (sin), cosine (cos), and tangent (tan). Sine is the ratio of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side.

  • What mnemonic is used to remember the relationships of trigonometric functions?

    -The mnemonic 'some old hags can't always hack their old age' helps remember the relationships: sine = opposite/hypotenuse, cosine = adjacent/hypotenuse, tangent = opposite/adjacent.

  • How do you solve for an unknown side length in a right-angle triangle using trigonometry?

    -To solve for an unknown side, you first determine which trigonometric function to use based on the given angle and sides. You then set up an equation using the function's formula, substitute the known values, and solve for the unknown side.

  • How do you calculate an unknown angle in a right-angle triangle using trigonometry?

    -To calculate an unknown angle, you set up an equation with the sine, cosine, or tangent function based on the known sides. Then, use the inverse function (sin-1, cos-1, or tan-1) on a calculator to solve for the angle.

  • What are the steps involved in using trigonometric functions to solve problems?

    -The steps involve identifying the known and unknown sides or angles, selecting the appropriate trigonometric function, setting up the equation, substituting the known values, and solving for the unknown quantity.

  • Can you provide an example of solving for a side length using the sine function?

    -For a triangle with a known angle of 35 degrees and a hypotenuse of 12 meters, to find the opposite side, set up the equation sin(35) = opposite/12. Solve for the opposite by multiplying sin(35) by 12, which gives the length of the opposite side.

  • What does the video suggest about learning trigonometry?

    -The video suggests that learning trigonometry can be straightforward with the proper approach, such as using mnemonics and understanding the basic concepts of trigonometric ratios and functions.

Outlines
00:00
📚 Introduction to Trigonometry

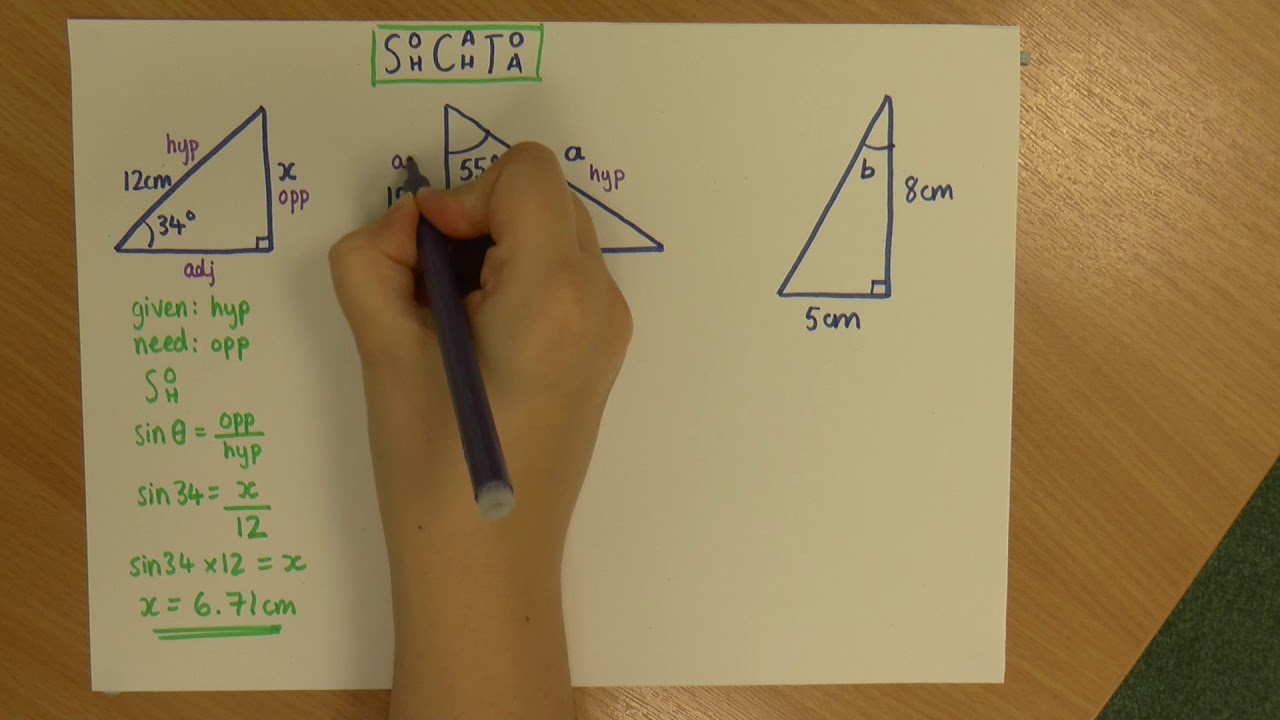
The first paragraph introduces the viewer to the topic of trigonometry, emphasizing its role in studying the relationships between the sides and angles of a right-angle triangle. It explains the fundamental concept that trigonometry allows us to find unknown side lengths or angles by using known values. The paragraph also outlines the three primary trigonometric functions: sine, cosine, and tangent, which are ratios of the sides of a triangle relative to an angle. A mnemonic is provided to help remember these functions: 'SOH CAH TOA', which stands for 'Sine equals Opposite over Hypotenuse, Cosine equals Adjacent over Hypotenuse, Tangent equals Opposite over Adjacent'. The paragraph concludes with the setup for solving a trigonometric problem using these functions.

05:02
🔍 Applying Trigonometry to Solve for Sides

The second paragraph delves into applying trigonometric functions to solve for unknown sides of a right-angle triangle. It begins with an example involving a triangle with a 35° angle and a known side length of 12 meters. The sine function is used to find the length of the opposite side. The process involves setting up the sine equation, substituting the known values, and solving for the unknown side length, which is found to be 6.88 meters. The paragraph then moves on to another example with a 48° angle and a known side length of 15 meters, using the tangent function to find the adjacent side length, which is determined to be 1.51 meters. The explanation includes a trick for solving equations and emphasizes the simplicity of trigonometric calculations.

10:03
📐 Finding Angles from Side Lengths

The third paragraph focuses on how to find an unknown angle in a right-angle triangle when two side lengths are known. It starts with an example where the side lengths are 105 meters and 33 meters, and the goal is to find the angle opposite the 33-meter side. The sine function is used again, and the process involves calculating the ratio of the opposite side to the hypotenuse, which is then used to find the angle using the inverse sine function on a calculator. The result is an angle of 18.3 degrees. The paragraph continues with another example involving a triangle with side lengths of 17 and 12 meters, where the cosine function is used to find the angle. The cosine of the angle is calculated, and the inverse cosine function is applied to find the angle, which is 45.1 degrees. The paragraph concludes with a reminder to be familiar with the calculator's functions for solving trigonometric problems and an invitation for viewers to request more videos on trigonometry if they encounter difficulties.

Mindmap
Keywords
💡Trigonometry
Trigonometry is a branch of mathematics that studies the relationships between the sides and angles of triangles, specifically right-angled triangles. In the video, it is introduced as the main subject and explored through various examples and problems. The presenter uses trigonometry to demonstrate how angles and side lengths can be determined through mathematical ratios derived from the triangle's dimensions.
💡Right Angle Triangle
A right angle triangle is a triangle in which one of the angles is a right angle (i.e., 90 degrees). The video centers around this type of triangle, showing how trigonometric functions apply specifically to its sides and angles. The structure of the right angle triangle allows for the use of trigonometric ratios such as sine, cosine, and tangent to solve problems.
💡Theta
Theta is commonly used in mathematics to denote an unknown angle, particularly in trigonometry and calculus. In the video, Theta is used to represent the angle in the triangle being analyzed. It serves as a placeholder for the angle that viewers learn to calculate using trigonometric functions.
💡Hypotenuse
The hypotenuse is the longest side of a right-angled triangle, opposite the right angle. In the script, it is specifically discussed and labeled as 'H', serving as a critical component in calculating the ratios for sine and cosine functions. Understanding the hypotenuse is crucial for solving trigonometric problems involving right triangles.
💡Opposite
In the context of trigonometry, the 'opposite' side of a triangle refers to the side opposite to the angle Theta being considered. The video explains how to identify the opposite side and use it, along with the hypotenuse or the adjacent side, to calculate trigonometric functions like sine and tangent.
💡Adjacent
Adjacent, in trigonometry, refers to the side of a right-angled triangle that is next to the angle Theta and not the hypotenuse. The video uses the adjacent side to demonstrate calculations involving the cosine and tangent functions. The understanding of which side is adjacent is crucial for applying the correct trigonometric function.
💡Sine, Cosine, Tangent
Sine, cosine, and tangent are fundamental trigonometric functions that relate the angles of a triangle to the ratios of its sides. The video explores these functions extensively, showing how sine is the ratio of the opposite side to the hypotenuse, cosine is the ratio of the adjacent side to the hypotenuse, and tangent is the ratio of the opposite side to the adjacent side. These functions are key to solving the trigonometric problems presented.
💡Mnemonic
A mnemonic is a memory aid used to enhance recall. In the script, a mnemonic 'Some Old Hags Can't Always Hack Their Old Age' is provided to help remember the formulas for sine, cosine, and tangent. This tool is valuable in educational videos like this to help viewers remember complex information more easily.
💡Solving Trigonometric Equations
The process of solving trigonometric equations involves finding the values of unknown angles or side lengths in triangles using trigonometric functions. The video guides viewers through several examples of how to label the sides, choose the appropriate trigonometric function, and manipulate equations to find the desired values.
💡Calculator Use
The use of a calculator is essential in trigonometry for evaluating trigonometric functions at various angles, a point emphasized in the video. Viewers are shown how to input values and use the inverse functions (like sin-1, cos-1) on a calculator to solve for angles, illustrating a practical aspect of learning trigonometry.
Highlights

Introduction to trigonometry and its focus on the relationships between the sides and angles of a right-angle triangle.

Explanation of how trigonometry allows the calculation of unknown side lengths and angles using known values.

Labeling of sides in a right-angle triangle as hypotenuse (h), opposite (o), and adjacent (a).

Description of the three main trigonometric functions: sine (sin), cosine (cos), and tangent (tan).

Memory aid for trigonometric functions using the phrase 'Some old hags can't always hack their old age'.

Process of solving a trigonometric problem by first labeling unknown sides and then choosing the appropriate trigonometric function.

Example problem solving where an angle of 35° and a side length of 12 units are used to find an unknown side length.

Use of the sine function to solve for the unknown side length in a right-angle triangle with a given angle and hypotenuse.

Second example problem involving an angle of 48°, a known side length, and the application of the tangent function to find an unknown side length.

Technique for solving trigonometric equations by creating a 'friendly equation' to assist in isolating the variable.

Method for finding an unknown angle from two known side lengths using the sine function and inverse functions on a calculator.

Calculation of an unknown angle in a right-angle triangle with side lengths of 105 and 33 units.

Explanation of how to use the cosine function to find an angle when the adjacent side and hypotenuse are known.

Final example problem with side lengths of 17 and 12 units, using the cosine function and its inverse to find the angle.

Emphasis on the importance of knowing how to use the calculator for solving trigonometric problems.

Invitation for viewers to ask questions or request more videos on trigonometry if they encounter difficulties.

Encouragement for viewers to like, subscribe, and support the TechMath channel for more educational content.

Transcripts

Browse More Related Video

Trig - 0.6 Trig Functions of Acute Angles

Trigonometry: Finding missing sides and angles

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

When Do I use Sin, Cos or Tan?

Trigonometry For Beginners!

Finding Sides and Angles with Right Triangle Trigonometry (Precalculus - Trigonometry 31)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
TrigonometryMath TutorialRight TriangleSine FunctionCosine FunctionTangent FunctionMath EducationAngle CalculationTriangle SidesEducational Video