Trigonometry
TLDRThis comprehensive video script serves as an educational guide for students preparing to study trigonometry, focusing on the essential concept of SOHCAHTOA. The acronym is a mnemonic device that aids in remembering the trigonometric ratios for sine, cosine, and tangent, which are fundamental for solving problems involving right triangles. The script explains how to apply these ratios to find missing sides of triangles and calculate the values of the trigonometric functions for a given angle. It also delves into the use of the Pythagorean theorem for finding missing sides and introduces special right triangles for quick reference. The video further explores the concept of reference angles and how to evaluate trigonometric functions for angles greater than 90 degrees or those not between 0 and 90 degrees. It concludes with a discussion on the signs of trigonometric functions in different quadrants, using the mnemonic 'all students take calculus' to help students remember which functions are positive in each quadrant. The script is a valuable resource for those looking to enhance their understanding of trigonometry and prepare for exams or coursework in the subject.
Takeaways
- 📚 The acronym SOHCAHTOA helps remember the trigonometric ratios: sine (opposite/hypotenuse), cosine (adjacent/hypotenuse), and tangent (opposite/adjacent).
- 🔢 For a 3-4-5 right triangle, sine of the angle is 4/5, cosine is 3/5, and tangent is 4/3.
- 🔴 To find missing sides of a right triangle, apply the Pythagorean theorem: a² + b² = c², where c is the hypotenuse.
- 📐 Special right triangles to memorize include 3-4-5, 5-12-13, and others which are multiples of these, like 7-24-25 and 9-40-41.
- 🧮 To find the trigonometric ratios without a calculator, use the properties of special triangles or the unit circle.
- 📈 The signs of the trigonometric functions depend on the quadrant of the angle: all positive in Q1, only sine in Q2, only tangent in Q3, and only cosine in Q4.
- 📉 The reference angle is the acute angle formed by the terminal side of the angle and the x-axis, which helps in finding the values of trigonometric functions for angles greater than 90 degrees.
- 🔁 Coterminal angles, which are angles that share the same terminal side, can be found by adding or subtracting multiples of 360 degrees.
- 🤓 The phrase 'all students take calculus' helps to remember the signs of the trigonometric functions in different quadrants.
- ✅ To rationalize a fraction with a square root in the denominator, multiply the numerator and denominator by the square root in the denominator.
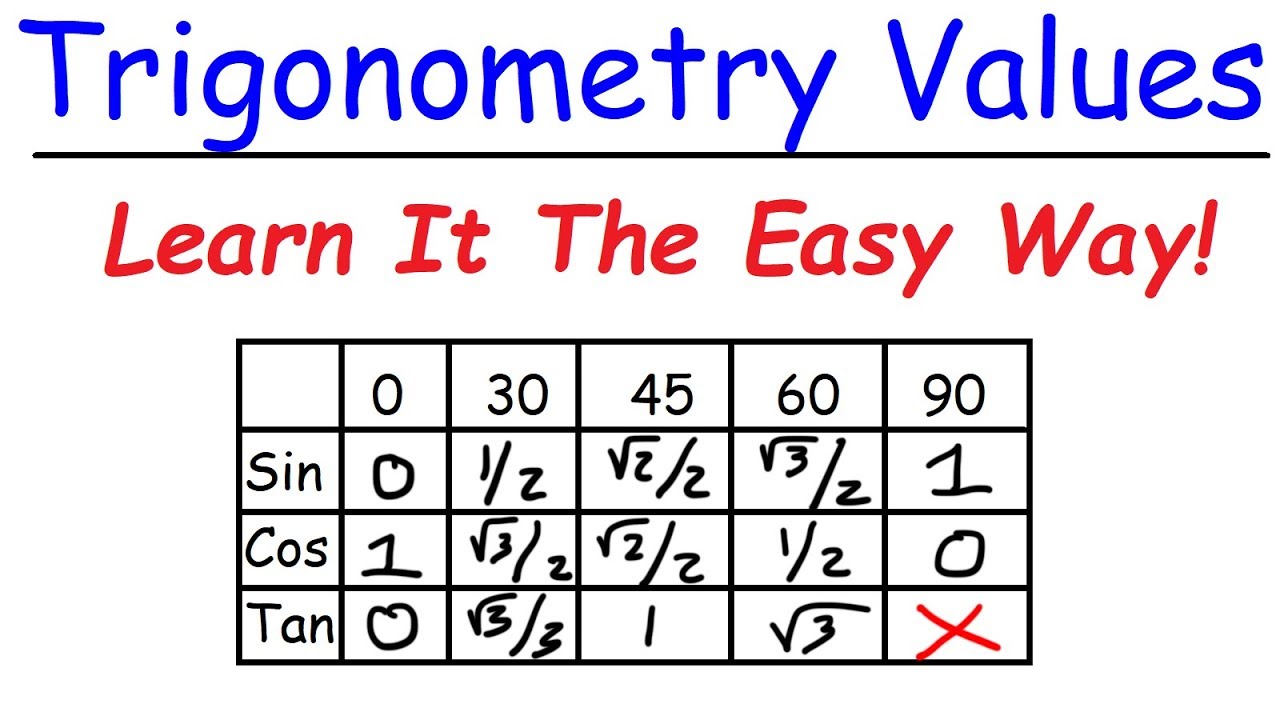
- 🔢 The exact values of common trigonometric functions, like sine of 30 degrees or cosine of 45 degrees, can be found using special triangles and without a calculator.
Q & A
What is the acronym 'sohcahtoa' used for in trigonometry?
-The acronym 'sohcahtoa' is used in trigonometry to help remember the formulas for the three most common trigonometric ratios: sine (SO), cosine (CA), and tangent (TOA).
What does the 'SOH' part of the sohcahtoa acronym stand for?
-The 'SOH' part of the sohcahtoa acronym stands for 'sine is opposite over hypotenuse', which is a way to remember the formula for sine in a right triangle.
How do you find the cosine of an angle in a right triangle?
-To find the cosine of an angle in a right triangle, you use the formula 'cosine is adjacent over hypotenuse', which means you divide the length of the side adjacent to the angle by the length of the hypotenuse.
What is the tangent ratio in a right triangle?
-The tangent ratio in a right triangle is found by dividing the length of the opposite side by the length of the adjacent side, as represented by the 'TOA' part of the sohcahtoa acronym.
How can you find the missing side of a right triangle if you know two sides?
-You can find the missing side of a right triangle using the Pythagorean theorem, which states that the square of the hypotenuse (c) is equal to the sum of the squares of the other two sides (a and b): c² = a² + b².
What are some special right triangles that you should memorize for trigonometry?
-Some special right triangles to memorize include the 3-4-5, 5-12-13, 8-15-17, 7-24-25, and 9-40-41 triangles, as they are commonly used in trigonometric calculations.
How do you find the cosecant, secant, and cotangent of an angle?
-Cosecant is the reciprocal of sine, secant is the reciprocal of cosine, and cotangent is the reciprocal of tangent. So, if you know the values of sine, cosine, and tangent, you can find their reciprocals to get cosecant, secant, and cotangent.
What is the reference angle in a trigonometry problem?
-The reference angle is the acute angle formed by the terminal side of the given angle and the x-axis. It is used to determine the signs of the trigonometric functions when dealing with angles greater than 90 degrees or not between 0 and 90 degrees.
How do you determine the signs of the trigonometric functions in different quadrants?
-The mnemonic 'all students take calculus' can help remember the signs: All (Sine, Cosine, and Tangent) are positive in Quadrant 1; Students (only Sine) is positive in Quadrant 2; Take (only Tangent) is positive in Quadrant 3; and Calculus (only Cosine) is positive in Quadrant 4.
What is the exact value of sine 30 degrees without using a calculator?
-The exact value of sine 30 degrees is 1/2, which can be determined by using the 30-60-90 special right triangle.
How do you convert an angle from radians to degrees?
-To convert an angle from radians to degrees, you multiply the angle in radians by the conversion factor 180/π.
What is the concept of coterminal angles in trigonometry?
-Coterminal angles are angles that share the same terminal side and therefore have the same trigonometric function values. They are found by adding or subtracting full rotations (360 degrees or 2π radians) to the original angle.
Outlines
📚 Introduction to Trigonometry Concepts
This paragraph introduces the audience to trigonometry, specifically for those studying it in high school or college. It explains the acronym SOHCAHTOA, which is a mnemonic for remembering the trigonometric ratios of sine, cosine, and tangent. The paragraph delves into how these ratios relate to the sides of a right triangle, specifically the opposite, adjacent, and hypotenuse with respect to an angle theta. An example using a 3-4-5 triangle is provided to illustrate the calculation of these ratios.
🔢 Applying Trigonometric Ratios in a Right Triangle
The paragraph continues the discussion on trigonometric ratios by showing how to apply them to find the sine, cosine, and tangent of an angle in a right triangle when two sides are given. It explains the use of the Pythagorean theorem to find the missing side of the triangle. The example triangle has sides of length 5 and 12, and the process to find the hypotenuse and subsequently the trigonometric ratios is demonstrated. The paragraph also touches on the concept of special right triangles and their memorization for quick calculations.
📐 Evaluating Trigonometric Ratios with Special Triangles
This section focuses on the use of special right triangles to simplify the evaluation of trigonometric ratios. It provides examples of such triangles, including the 3-4-5, 5-12-13, and others, emphasizing their utility in avoiding the use of the Pythagorean theorem. The paragraph also explains how to handle trigonometry problems where the ratios are given and the angle is between 0 and 90 degrees, using the example of a triangle with a sine ratio of 8/17.
🤔 Dealing with Non-Special Triangles and Quadrants
The paragraph discusses the approach to finding trigonometric ratios when dealing with non-special triangles and angles that fall in different quadrants. It explains the use of the Pythagorean theorem to find missing sides and the importance of considering the quadrant to determine the signs of the ratios. An example is given where sine theta equals 2/5, and the angle is between pi/2 and pi, leading to the use of the Pythagorean theorem and consideration of the triangle's location in quadrant two.
📐 Rationalizing Trigonometric Expressions
This part of the script covers the process of rationalizing trigonometric expressions, particularly when the denominator contains a square root. It explains how to multiply the numerator and denominator by the square root to achieve a rationalized form. The paragraph also covers finding the cosecant, secant, and cotangent ratios for the given triangle, demonstrating the process with examples.
🔢 Exact Values of Trigonometric Functions
The paragraph explores how to find the exact values of trigonometric functions for specific angles without a calculator. It introduces the concept of special right triangles, such as the 30-60-90 triangle, and how to use them to evaluate functions like sine 30 and cosine 60. It also explains how to convert angles from radians to degrees and use the unit circle for such evaluations.
🤔 Evaluating Trigonometric Functions for Larger Angles
This section deals with evaluating trigonometric functions for angles greater than 90 degrees. It explains the concept of a reference angle, which is the acute angle formed between the terminal side of the angle and the x-axis. The paragraph demonstrates how to use the reference angle to find the values of sine, cosine, and tangent for angles in different quadrants, using examples like sine of 240 degrees and cosine of 150 degrees.
📐 Understanding Signs of Trigonometric Functions in Quadrants
The paragraph discusses the signs of trigonometric functions in different quadrants using the mnemonic 'all students take calculus.' It explains which functions are positive in each quadrant and relates the signs to the coordinates of points within those quadrants. The concept of tangent as y/x and its implications for the signs of the functions is also covered, along with an example of evaluating tangent at negative 120 degrees.
🔢 Working with Cosecant and Secant Functions
This section covers the evaluation of cosecant and secant functions for angles in specific quadrants. It explains that secant is the reciprocal of cosine and cosecant is the reciprocal of sine. The paragraph provides examples of finding the secant of 225 degrees and cosecant of negative 13 pi/6, including the process of converting angles from radians to degrees and dealing with negative angles and coterminal angles.
📝 Conclusion and Further Resources
The final paragraph wraps up the video by summarizing the content covered and encouraging viewers to check out additional trigonometry resources in the video description. It also prompts viewers to subscribe to the channel and turn on notifications to stay updated with new content.
Mindmap
Keywords
💡Trigonometry
💡SOHCAHTOA
💡Right-angled triangle
💡Pythagorean theorem
💡Sine, Cosine, Tangent
💡Special right triangles
💡Quadrants
💡Reference angle
💡Unit circle
💡Radians and degrees
💡Reciprocal trigonometric functions
💡Coterminal angles
Highlights
The video introduces the SOHCAHTOA mnemonic to remember the trigonometric ratios for sine, cosine, and tangent.
Sine of an angle is the ratio of the opposite side to the hypotenuse in a right triangle.
Cosine is the ratio of the adjacent side to the hypotenuse in a right triangle.
Tangent is the ratio of the opposite side to the adjacent side in a right triangle.
Demonstration of how to calculate sine, cosine, and tangent for a 3-4-5 right triangle.
Explanation of how to find the missing side of a right triangle using the Pythagorean theorem.
Procedure to calculate the trigonometric ratios for a right triangle with sides of length 5, 12, and 13.
Discussion of special right triangles that should be memorized for quick reference.
Method to find the values of sine, cosine, and tangent without using the Pythagorean theorem for special triangles.
Calculation of cosecant, secant, and cotangent as reciprocals of sine, cosine, and tangent, respectively.
Approach to find the value of cosine and tangent when given the sine of an angle and its quadrant.
Use of the unit circle and conversion from radians to degrees for evaluating trigonometric functions at specific angles.
Explanation of how to evaluate trigonometric functions for angles greater than 90 degrees using reference angles.
Introduction of the 'ALL STUDENTS TAKE CALCULUS' mnemonic to determine the sign of trigonometric functions in different quadrants.
Process to find the exact value of sine for 30 degrees using the 30-60-90 special right triangle.
Method to evaluate trigonometric functions for negative angles or angles greater than 360 degrees using coterminal angles.
Final example calculating the value of secant for 225 degrees using a 45-45-90 reference triangle.
Summary and invitation to subscribe to the channel for more trigonometry content and example problems.
Transcripts
Browse More Related Video

Trigonometry For Beginners!

Introduction to Right Triangle Trigonometry (Precalculus - Trigonometry 30)

How To Find The Exact Values of Trig Functions

Trigonometric Functions of Any Angle - Unit Circle, Radians, Degrees, Coterminal & Reference Angles
A Simple Trick To Remember Trigonometry Values

Trigonometry: How to use the ASTC Rule | The Quadrant | CAST
5.0 / 5 (0 votes)
Thanks for rating: