Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics

Science Ready
8 Nov 202113:34
EducationalLearning
32 Likes 10 Comments

TLDRThis video delves into the concept of gravitational potential energy, explaining its definition and the formula U = mgh, where U is the potential energy, m is mass, g is gravitational acceleration, and h is height. It clarifies that g is not constant and varies with the Earth's mass, radius, and shape. The video introduces a more accurate formula U = -GMm/r, where G is the gravitational constant, M is Earth's mass, and r is the distance from the center of the Earth. It corrects the misconception that potential energy decreases with increasing distance from a gravitational source and demonstrates how to calculate the work done in moving an object against gravity, using a satellite as an example.

Takeaways
  • 🌌 Gravitational potential energy (U) is defined as the energy that an object possesses due to its position in a gravitational field, specifically at a height 'h' above the ground.
  • ⚖️ The formula U = mgh calculates potential energy where 'm' is mass, 'g' is gravitational acceleration, and 'h' is height. This assumes 'g' is constant, which is only true near Earth's surface.
  • 📏 The value of 'g' varies based on altitude, Earth's crust density, and its elliptical shape, which affects calculations of gravitational potential energy over larger distances.
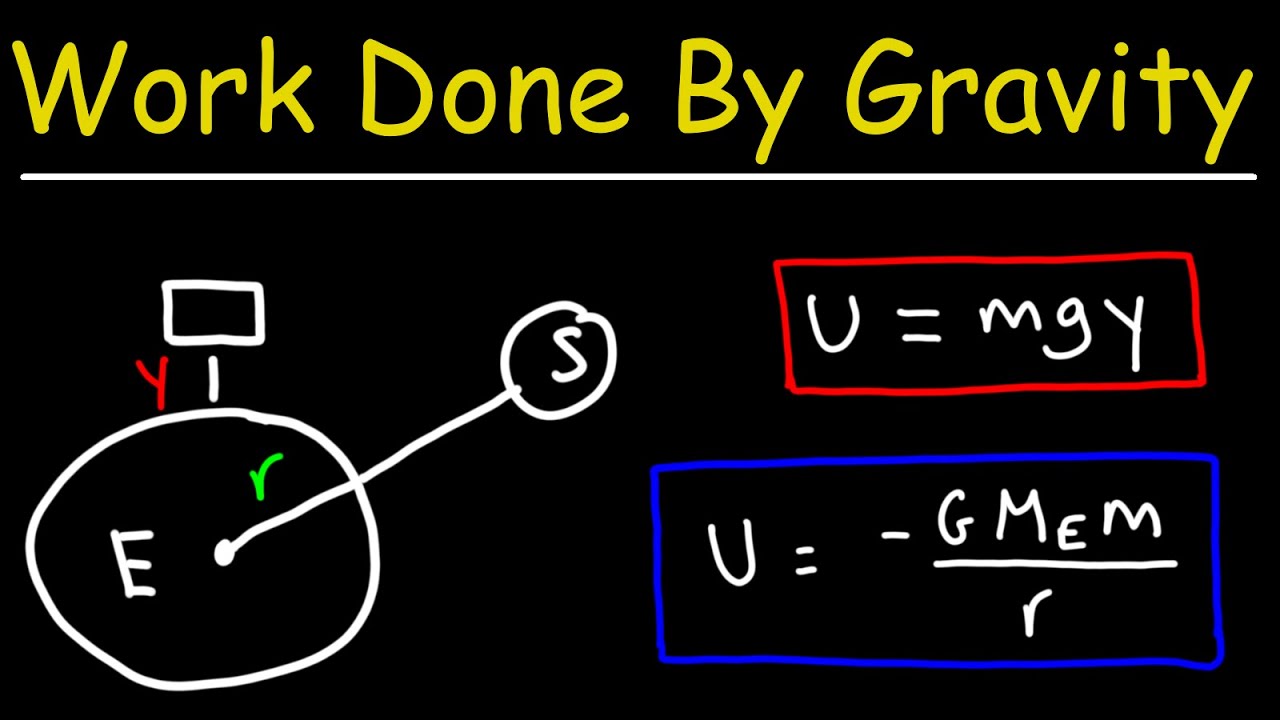
  • 🔄 When considering larger distances from Earth's center, the more accurate formula U = -GMm/R should be used, where 'G' is the universal gravitational constant, 'M' the Earth's mass, 'm' the object's mass, and 'R' the distance from Earth's center.
  • 🔍 To address inconsistencies in gravitational potential energy when 'R' increases (implying energy should increase), the reference point of the potential energy equation is shifted to infinity where U is zero.
  • ➖ By introducing a negative sign in the new potential energy formula, it ensures that as an object moves closer to a gravitational source (decreasing 'R'), its potential energy decreases, becoming more negative.
  • 📈 The relationship between the distance 'R' from Earth and gravitational potential energy is hyperbolic, meaning U approaches zero as 'R' increases towards infinity, and becomes more negative as 'R' decreases.
  • 🚀 For practical applications like moving a satellite, the change in potential energy (work done) can be calculated using the difference in U at two different points, using the formula W = U_final - U_initial.
  • 🛰️ A practical example: moving a satellite from 300 km to 4,000 km above Earth requires calculating the change in gravitational potential energy to determine the work needed for such movement.
  • 🧮 The modified gravitational potential energy formula better accommodates variations in gravitational strength over different distances, making it essential for accurate space-related calculations.
Q & A

  • What is gravitational potential energy?

    -Gravitational potential energy is the amount of work that can be done by gravity at a particular height h. It is the energy an object possesses due to its position in a gravitational field.

  • How is gravitational potential energy calculated for an object near the Earth's surface?

    -The gravitational potential energy (U) of an object with mass (m) at a height (h) above the Earth's surface is calculated using the formula U = mgh, where g is the acceleration due to gravity.

  • What factors affect the value of gravitational acceleration (g) on Earth?

    -The value of g on Earth is affected by the distance from the Earth's center (altitude), the Earth's crust density, and the Earth's shape (it being slightly elliptical).

  • Why is the simple formula for gravitational potential energy (U = mgh) not always accurate?

    -The simple formula U = mgh assumes that g is a constant, which is not true as g varies with altitude, crust density, and Earth's shape. Therefore, for large distances or varying gravitational fields, a more accurate equation is needed.

  • What is the modified formula for gravitational potential energy that accounts for the variability of g?

    -The modified formula for gravitational potential energy is U = -(GMm)/r, where G is the gravitational constant, M is the mass of the Earth, m is the mass of the object, and r is the distance between the center of the Earth and the object.

  • Why is the reference point for gravitational potential energy changed to infinity in the modified equation?

    -The reference point is changed to infinity to account for the decrease in gravitational acceleration as the object moves further away from the Earth. At infinity, the gravitational potential energy is defined as zero because the gravitational acceleration is zero.

  • How does the relationship between gravitational potential energy and distance (radius r) appear graphically?

    -The relationship between gravitational potential energy (U) and distance (radius r) is hyperbolic and inversely proportional. As r increases, U approaches zero, and as r decreases, U becomes more negative.

  • What is the definition of gravitational potential energy in the context of the modified equation?

    -In the context of the modified equation, gravitational potential energy is the energy required to move a mass from a point at infinity (where gravitational potential energy is zero) to a point within the gravitational field at a distance r from the source of gravity.

  • How can we calculate the work done to move a mass within a gravitational field?

    -The work done (W) to move a mass from point p to point q within a gravitational field is equal to the change in gravitational potential energy, calculated as W = U_final - U_initial, using the modified gravitational potential energy formula.

  • What is the work done to move a satellite from an altitude of 300 km to 4000 km above the Earth's surface?

    -The work done to move a 200 kg satellite from an altitude of 300 km to 4000 km above the Earth's surface is 4.28 x 10^9 joules, as calculated using the modified gravitational potential energy formula and the given values.

  • How does the concept of gravitational potential energy relate to the conservation of energy?

    -The concept of gravitational potential energy is closely related to the conservation of energy. When work is done on an object to move it against gravity (increasing its gravitational potential energy), that energy is stored and can be released when the object is allowed to fall back towards the source of gravity.

Outlines
00:00
🌌 Understanding Gravitational Potential Energy

This section explains gravitational potential energy, which is the work gravity can perform at a specific height. By lifting a ball of mass 'm' to height 'h', the potential energy 'U' is calculated as U = mgh, where 'g' is gravitational acceleration. The energy can be perceived in two ways: the work gravity could do if the ball drops or the work required to raise it from the ground to that height. The section also details how gravitational acceleration 'g' is not constant and varies with altitude, crust density, and Earth's elliptical shape. As 'g' changes with distance from Earth's center, the gravitational potential energy formula needs adjusting, using more precise values for 'g' over larger distances. The revised formula for potential energy over larger distances involves substituting 'g' with GM/r², where 'G' is the gravitational constant, 'M' the Earth's mass, and 'r' the distance to Earth's center, adding a negative sign to align with physical observations that potential energy increases as distance from Earth increases.

05:01
🚀 Advanced Gravitational Potential Energy Equations

This segment introduces a more refined equation for gravitational potential energy using infinity as the reference point where the potential energy is zero. This model explains that as an object moves away from a gravitational source, its potential energy should increase and become less negative, contrary to what simpler models suggest. The relationship between distance 'r' and gravitational potential energy is hyperbolic, showing that potential energy approaches zero as 'r' tends to infinity. The section applies this concept to practical scenarios such as moving a rocket from one point to another within Earth's gravitational field, explaining the computations of work done based on changes in the gravitational potential energy. The advanced formula provides a more accurate representation for large-scale gravitational interactions, essential for understanding satellite movements and other space-related activities.

10:01
🛰️ Practical Application: Satellite Gravitational Potential Energy

This section applies the concepts of gravitational potential energy to a practical scenario involving a satellite. The satellite's gravitational potential energy at an altitude of 300 kilometers above Earth is calculated using the advanced formula U = -GMm/r, taking into account the Earth's radius and the satellite's altitude to find 'r'. The calculation of work needed to move the satellite to a higher altitude of 4000 kilometers is detailed, showing how potential energy changes with altitude. The increase in altitude leads to higher potential energy, requiring positive work to achieve. The process involves calculating the difference in gravitational potential energy at the two altitudes to determine the work done, illustrating how energy conservation principles apply in moving objects within gravitational fields.

Mindmap
Keywords
💡Gravitational Potential Energy
Gravitational potential energy is the energy an object possesses due to its position in a gravitational field. It is defined as the amount of work that can be done by gravity at a particular height h. In the context of the video, this energy is associated with the work done to lift an object against gravity, such as bringing a ball upwards vertically, which increases its potential energy.
💡Work
Work, in the context of physics, is the amount of energy transferred by a force acting over a distance. It is a measure of energy and is done when an object is moved by an external force, such as gravity, over a displacement. In the video, work is discussed in terms of the positive work required to lift an object against gravity and the work done by gravity when an object is dropped.
💡Gravitational Acceleration (g)
Gravitational acceleration, denoted as 'g', is the acceleration due to gravity that affects the motion of objects near the Earth's surface. It is a constant value on Earth (approximately 9.81 m/s^2), but it can vary depending on location and altitude. The video explains that the value of 'g' is not constant and can change with the mass of the Earth, its radius, and the distance from the Earth's center.
💡Height (h)
Height (h) in the context of gravitational potential energy refers to the vertical distance an object is lifted or displaced from its original position. The greater the height, the more work is required to lift the object, and consequently, the higher the gravitational potential energy.
💡Mass (m)
Mass (m) is a measure of the amount of matter in an object. In the context of gravitational potential energy and work, the mass of an object determines the amount of force exerted on it by gravity and thus the amount of work done in lifting or moving the object within a gravitational field.
💡Earth's Gravitational Field
The Earth's gravitational field is the region around the Earth where its gravitational force affects objects. This field is responsible for the gravitational potential energy and work experienced by objects within it. The strength of the gravitational field can vary depending on the distance from the Earth's center and the Earth's shape.
💡Reference Point
A reference point is a point used as a baseline or starting point for comparison. In the context of gravitational potential energy, the reference point is typically the point at infinity, where the gravitational potential energy is considered to be zero. This concept is used to derive a more accurate equation for gravitational potential energy that accounts for the variability of 'g'.
💡Radius (r)
Radius (r) is the distance from the center of a sphere or circular shape to any point on its surface. In the context of the Earth and gravitational potential energy, the radius includes both the Earth's average radius and the altitude above the surface. The value of 'r' is crucial in determining the gravitational acceleration 'g' and the gravitational potential energy (U).
💡Law of Conservation of Energy
The Law of Conservation of Energy states that energy cannot be created or destroyed, only transformed from one form to another. In the context of the video, this law is applied to explain that the work done to move an object within a gravitational field is equal to the change in its gravitational potential energy.
💡Hyperbolic Relationship
A hyperbolic relationship is a mathematical relationship where two quantities are inversely proportional to each other. In the context of the video, it refers to the relationship between the radius (r) and gravitational potential energy (U), where as 'r' increases, the potential energy (U) approaches zero, and vice versa.
💡Rocket
A rocket is a vehicle designed to propel itself into space or another celestial body, often using controlled explosions to create thrust. In the context of the video, a rocket is used as an example of an object whose gravitational potential energy changes as it moves from one point within the Earth's gravitational field to another.
Highlights

Introduction to gravitational potential energy and its basic formula U = mgh.

Explanation of gravitational potential energy as work done by gravity or to counteract gravity.

Discussion on the variation of gravitational acceleration (g) with altitude, earth's crust density, and its shape.

Introduction to the revised gravitational potential energy formula incorporating changes in g due to varying distances from the earth's center.

Derivation of a new formula for gravitational potential energy using U = -GMm/R, adjusting for variable g.

Explanation of why gravitational potential energy decreases (becomes more negative) as an object approaches a gravitational source.

Introduction of infinity as a reference point in the revised gravitational potential energy equation to resolve logical inconsistencies.

Clarification on how gravitational potential energy increases as the distance from a gravitational source increases, approaching zero at infinity.

Comparison of the old and new gravitational potential energy equations and their applications over different scales.

Practical use of the new gravitational potential energy formula to calculate work needed to move masses within a gravitational field.

Detailed example calculating the gravitational potential energy of a satellite at a specific altitude using the new formula.

Step-by-step calculation of the work done to move a satellite from one altitude to a higher one.

Explanation of the conservation of energy principle in moving a satellite to a higher gravitational potential energy.

Simplification of the work done equation by factorizing and manipulating terms for practical computations.

Final energy requirement calculation for moving a satellite to a higher orbit, demonstrating the application of the new gravitational potential energy formula.

Transcripts

Browse More Related Video

13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics

Potential energy and gravity

Gravitational Potential Energy Calculations (GPE) - Mass x Gravity x Height OR GPE=mgh

Gravitational Potential Energy, Example Problems

Calculating gravitational potential energy | Modeling energy | High school physics | Khan Academy

Work Done By Gravity and Gravitational Potential Energy - Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
GravitationalEnergyPhysicsConceptsSatelliteOrbitRocketPropulsionWorkCalculationGravitationalFieldPotentialEnergyFormulaEarthRadiusSpaceTravelEnergyConservation