Potential energy and gravity

Physics with Professor Matt Anderson
17 Jun 201406:55
EducationalLearning
32 Likes 10 Comments

TLDRIn this educational discourse, Professor Anderson delves into the concepts of potential energy, energy, and gravity, particularly focusing on how potential energy is calculated when lifting an object against gravity. The traditional formula, MGH, is derived from integrating the force (mg) over the distance (H). However, when the gravitational force isn't constant, such as at high altitudes, the calculation becomes more complex. The professor introduces a method for calculating work done at varying gravitational forces, integrating the gravitational force over the distance from the Earth's center, resulting in a potential energy formula that depends on the final position relative to the Earth's center. This exploration enhances the understanding of energy dynamics in physics.

Takeaways
  • 📚 The concept of potential energy is introduced in the context of lifting a box to a higher position.
  • 🔢 The formula for potential energy is given as MGH, where M is the mass of the box, G is the acceleration due to gravity, and H is the height.
  • 🧮 The process of calculating potential energy involves integrating the force (mg) over the distance (H) lifted.
  • 🔄 When mg is constant, it can be taken out of the integral, simplifying the calculation to mgh.
  • 🌐 The gravitational force is not constant at very high altitudes and varies with the distance from the Earth's center.
  • 🚀 To calculate work done at varying gravitational forces, the force equation GMm/R^2 is used, where R is the distance from the center of the Earth.
  • 📈 The work done is the integral of the force along the displacement dr, from the initial position Ri to the final position Rf.
  • 🎯 The constants g, m, and M can be taken out of the integral, simplifying the expression for work done.
  • 🌌 The integral of 1/R^2 with respect to R results in -1/R, which is used to calculate the work done against gravity.
  • 📉 The potential energy is negative because the zero point is set at infinity, indicating that energy is required to move an object closer to a massive body like Earth.
  • 🔄 The approximation for potential energy when Ri is set to infinity simplifies the formula to focus on the final position Rf.
Q & A

  • What is potential energy in the context of lifting a box?

    -Potential energy in this context refers to the stored energy an object possesses due to its position in a gravitational field, specifically, its height above a reference point. When a box is lifted, it gains potential energy which can be expressed as MGH, where M is the mass of the box, G is the acceleration due to gravity, and H is the height the box is lifted to.

  • How is the work done in lifting a box related to its potential energy?

    -The work done in lifting a box is equal to the change in its potential energy. When you lift a box against gravity, you do work that is stored as potential energy in the box. The work done, which is the force (mg) times the distance (H), is the same as the potential energy (MGH) the box has once it's lifted.

  • Why can't we take mg out of the integral when it's not constant?

    -When lifting a box, if the gravitational force (mg) is constant, it can be taken out of the integral because it does not change with the distance (H). However, if the gravitational force is not constant—for example, at very high altitudes where the Earth's gravitational influence weakens—the force varies with distance, and thus it cannot be removed from the integral.

  • How does the gravitational force change with distance from the Earth's center?

    -The gravitational force, given by the equation F = G * (mass of Earth * mass of object) / R^2, decreases with the square of the distance (R) from the Earth's center. As you move farther from the Earth, the gravitational force becomes weaker, and thus the work done to overcome this force changes.

  • What is the formula for calculating the work done in lifting an object when gravitational force is not constant?

    -When gravitational force is not constant, the work done (W) in lifting an object is given by the integral from the initial position (Ri) to the final position (Rf) of the force (F) along the displacement (Dr). The formula is W = ∫(F * Dr) from Ri to Rf. For a variable gravitational force, F = G * (mass of Earth * mass of object) / R^2, and the integral becomes W = G * (mass of Earth * mass of object) * ∫(1/R^2 * dR) from Ri to Rf.

  • What is the result of the integral of 1/R^2 from Ri to Rf?

    -The integral of 1/R^2 with respect to R from Ri to Rf is -1/R (evaluated from Ri to Rf). This result is used to calculate the work done in lifting an object when the gravitational force is not constant.

  • How do we calculate the work done to move an object to a very far distance from the Earth?

    -To calculate the work done to move an object to a very far distance, we use the formula W = G * (mass of Earth * mass of object) * (1/Rf - 1/Ri), where Rf is the final distance from the Earth's center and Ri is the initial distance. This approximation assumes that the reference point for potential energy is set at infinity.

  • Why is the gravitational potential energy negative in the formula?

    -The gravitational potential energy is negative because we set the zero point of potential energy at infinity. Anything closer to a massive object, like the Earth, will have negative potential energy, indicating that work was done to move it against the gravitational force to that position.

  • What is the significance of setting the reference point for potential energy at infinity?

    -Setting the reference point for potential energy at infinity simplifies the calculation of potential energy, especially for objects far from the Earth. It allows us to focus on the final position (Rf) and the work done to reach that position, without having to consider the variable potential energy at different heights.

  • How does the concept of potential energy and work relate to objects in space?

    -In space, the concept of potential energy and work becomes crucial when considering the movement of spacecraft or objects near celestial bodies. The work done to overcome the gravitational pull of a planet or moon determines the energy required for propulsion, and the potential energy of an object in space can be converted back into kinetic energy as it falls back towards the celestial body.

  • What is the practical application of understanding variable gravitational force in space travel?

    -Understanding variable gravitational force is essential for accurate trajectory planning and fuel consumption estimation in space travel. It helps in determining the energy required to lift objects, such as spacecraft, from the Earth's surface to orbit and beyond, and it's critical for designing efficient space missions and ensuring the safety of astronauts.

Outlines
00:00
🌐 Introduction to Potential Energy and Gravity

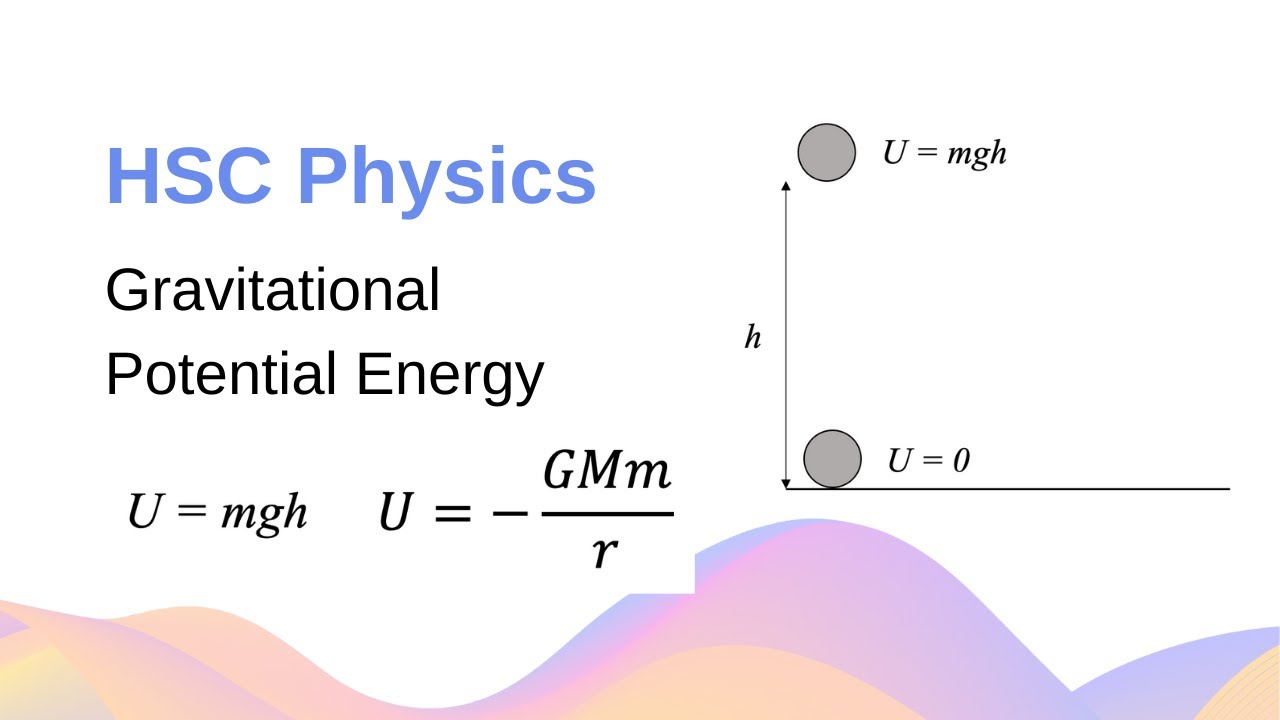
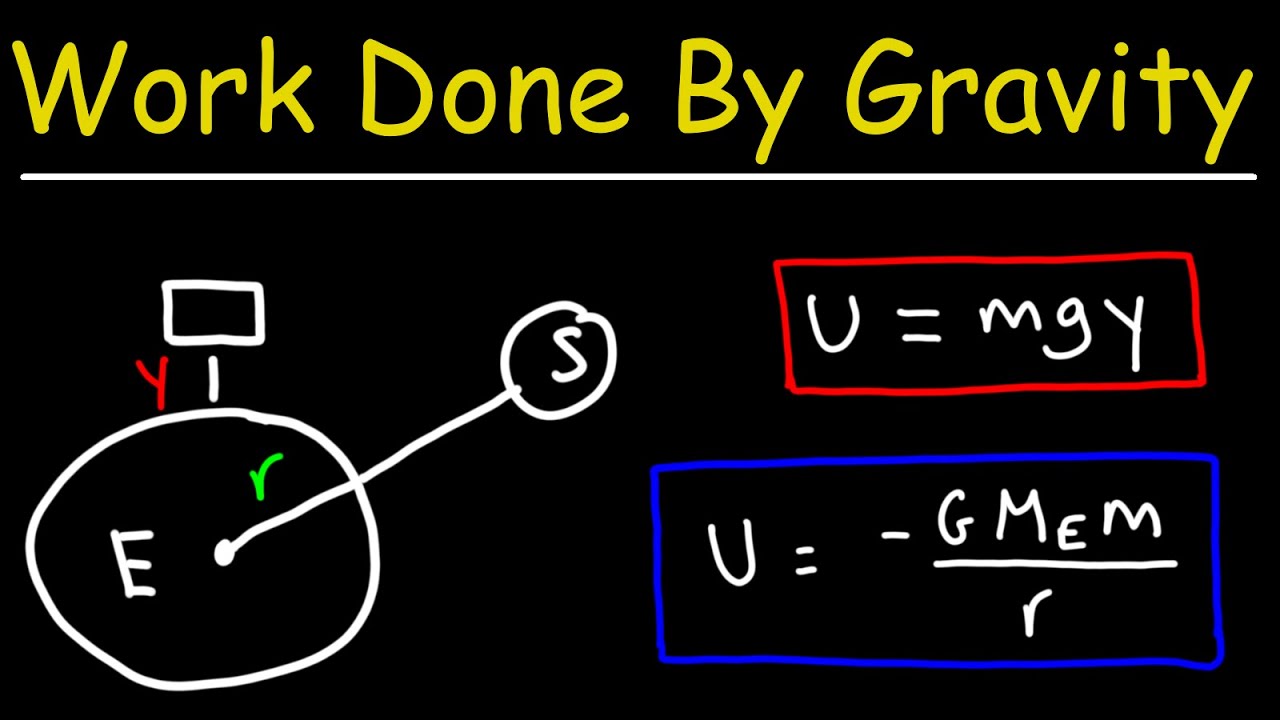
This paragraph introduces the concepts of potential energy, energy, and gravity, building upon previous discussions about the Earth. It explains how potential energy is associated with lifting a box and the work done in the process. The key formula mentioned is potential energy (PE) = MGH, where M is the mass of the object, G is the acceleration due to gravity, and H is the height. It also addresses the assumption that G is constant, which may not be accurate at very high altitudes, necessitating a more careful approach to calculating work done and potential energy at such elevations.

05:01
🔢 Calculating Work and Potential Energy at Different Heights

This paragraph delves into the calculation of work done and potential energy when lifting an object to a position far from the Earth's surface. It explains that the force exerted is equal to the gravitational force, which is the product of the Earth's mass (M) and the object's mass (m) divided by the square of the distance (R^2). The work done is then the integral of this force over the distance (Dr) from the initial to the final position. The calculation involves integrating the 1/R^2 term, resulting in the potential energy formula, which is expressed as the difference in potential energy (PE) from an infinite reference point to the final position (RF) minus the potential energy at the initial position (RI). The paragraph highlights the importance of considering the non-constant nature of gravitational force at different heights for accurate calculations.

Mindmap
Keywords
💡Potential Energy
Potential energy is the stored energy an object possesses due to its position relative to other objects, such as being lifted against gravity. In the video, potential energy is associated with lifting a box from one height to another, and it is calculated using the formula MGH, where M is the mass of the object, G is the acceleration due to gravity, and H is the height. The concept is central to understanding how work is done against gravity and how energy is stored or released in such processes.
💡Work
Work in physics is defined as the amount of energy transferred by a force acting over a distance. In the context of the video, work is done when lifting a box against gravity, which requires applying a force equal to the weight of the box (mg) and integrating this force over the distance (height) lifted. The work done is related to the change in potential energy of the object.
💡Gravity
Gravity is the force that attracts two bodies with mass towards each other. In the video, gravity is the force that acts on the box being lifted, and it is what the professor is trying to overcome by doing work on the box. The gravitational force is dependent on the masses of the objects and the distance between their centers, as described by the formula Gmm/R^2, where G is the gravitational constant, m and M are the masses of the objects, and R is the distance between their centers.
💡Integration
Integration is a mathematical process used to calculate the accumulated effect of a quantity over a given interval. In the video, integration is used to compute the work done when lifting a box, by summing up the effects of the gravitational force acting over the distance lifted. The integral of the force (mg) over the height (from 0 to H) gives the total work done.
💡Constant
In the context of the video, a constant is a value that does not change with the variables being considered. The acceleration due to gravity (g) is treated as a constant when it is the same at all heights considered. However, the professor points out that gravity is not always constant, especially at very high altitudes, which affects how the work done and potential energy are calculated.
💡Dot Product
The dot product is a mathematical operation that takes two vectors and returns a scalar. In physics, it is used to find the component of one vector in the direction of another. In the video, the dot product is mentioned in the context of work, which is the product of the force vector and the displacement vector. Since the force and displacement are in the same direction (upwards against gravity), the dot product simplifies to the product of the magnitudes of these vectors.
💡Gravitational Force
Gravitational force is the attractive force that exists between any two masses. In the video, the gravitational force is what acts on the object being lifted and is calculated using the formula Gmm/R^2, where G is the gravitational constant, m is the mass of the object, M is the mass of the Earth, and R is the distance from the center of the Earth to the object. This force is central to the discussion of potential energy and work done in lifting an object.
💡Altitude
Altitude refers to the height of an object above a reference point, typically the Earth's surface. In the video, altitude is discussed in the context of how the gravitational force changes with increasing distance from the Earth. As altitude increases, the gravitational force decreases, which in turn affects the work done and the potential energy of the object.
💡Reference Point
A reference point is a fixed point used as a basis for measurements or comparisons. In the context of the video, the professor discusses setting the reference point for potential energy at infinity, which simplifies the calculation of gravitational potential energy by making the zero point of energy at an infinite distance from the Earth.
💡Zero Point
The zero point, in the context of potential energy, is the reference level at which the potential energy is considered to be zero. In the video, the professor chooses to set the zero point at infinity, meaning that all potential energy calculations are relative to this point. This choice affects how the work done against gravity and the potential energy of an object are determined.
💡Approximation
An approximation is a simplified estimate or representation of a real value or object. In the video, the professor uses an approximation by setting the reference point for potential energy at infinity, which simplifies the potential energy calculation to a single term dependent only on the final position of the object. This approximation is useful for calculations involving large distances or high altitudes where the gravitational force changes significantly.
Highlights

Discussion on potential energy, energy, and gravity begins.

Review of previous concept where potential energy is associated with lifting a box and the formula MGH is introduced.

Explanation of the work done in lifting a box, which is the integral of the force over the distance.

Clarification that the simplification of the integral to MGH assumes that the mass of the box (m) and the gravitational force (g) are constant.

Introduction of the concept that gravitational force is not constant at very high altitudes.

The need for a more careful calculation of work done when lifting an object at high altitudes is emphasized.

Explanation of how to calculate the work done when lifting an object to a distance far from Earth, considering the variable gravitational force.

The work done is described as the integral of the gravitational force over the distance, with a dot product that simplifies due to the force and displacement being in the same direction.

The formula for gravitational force is given as GMm/R^2, where G is the gravitational constant, M is the mass of Earth, m is the mass of the object, and R is the distance from the center of Earth.

Integration of the gravitational force along the distance from the Earth's center (Dr) is discussed.

The integration process is detailed, with constants GMm pulled outside the integral and the integral of 1/R^2 evaluated from initial to final position.

The final formula for the work done in moving an object from one position to another is presented as GMm(1/Rf - 1/Ri).

An approximation is made by setting the reference point for potential energy at infinity.

The gravitational potential energy is then expressed as negative (because zero is set at infinity) and dependent only on the final position (Rf).

The concept that closer an object is to a massive body like Earth, the more negative its potential energy becomes, is highlighted.

Transcripts

Browse More Related Video

Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics

Work Done By Gravity and Gravitational Potential Energy - Physics

GCSE Physics - Gravity, Weight and GPE #3

Gravitational potential energy at large distances | AP Physics 1 | Khan Academy

What is Gravitational Potential Energy - a deeper understanding

13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Physics ConceptsGravitational ForcePotential EnergyWork CalculationAltitude EffectsEarth's GravityScientific ExplanationLifting ObjectsIntegration in PhysicsMGH Formula