13.3a Gravitational Potential Theory | A2 G-Fields | Cambridge A Level Physics
TLDRThis script delves into the concept of gravitational potential and gravitational potential energy (GPE), explaining their relationship with work done and the force of gravity. It begins with a thought experiment, visualizing a sphere on a trampoline to illustrate the idea of potential energy. The video clarifies that GPE is the work done to bring a unit mass from infinity to a point, and its equation is negative GMm/r, where G is the gravitational constant, M is the mass of the Earth, m is the mass of the object, and r is the distance from the center of the Earth. The script also explains how the change in GPE is related to the work done against gravitational forces, and why it is negative. The video uses a simulation to visually demonstrate how gravitational potential changes with distance and mass, emphasizing the concept of a gravitational well. Overall, the script aims to provide a deeper understanding of these fundamental physics concepts.
Takeaways
- 🌌 The concept of gravitational potential energy is introduced as the work done to bring a mass from infinity to a point.
- 📉 Gravitational potential energy (GPE) is calculated using the formula U = -G * (m1 * m2) / r, where G is the gravitational constant, m1 and m2 are the masses, and r is the distance between the centers of the two masses.
- 🔄 The change in gravitational potential energy is given by the final potential energy minus the initial potential energy, often simplified as mgh near the Earth's surface.
- 🌐 Gravitational potential, denoted by phi (ϕ), is the work done per unit mass to bring a unit mass from infinity to a point, and is given by the formula ϕ = -G * m / r.
- 📊 The graph of gravitational potential shows a negative value at infinity and becomes more negative as one gets closer to the source of gravity, indicating a 'potential well'.
- 🏋️♂️ Gravitational forces are attractive, which is why the work done against gravity (to move a mass closer to the source) is considered negative work.
- 🔄 The gravitational potential at a point is the sum of the potentials due to all masses at that point, which can result in stable points where forces balance out.
- 🌍 The Earth's gravitational potential well is what keeps objects on its surface and causes them to 'stick' to the planet.
- 🪐 The concept of gravitational potential and potential energy is crucial for understanding the motion of satellites and other celestial bodies.
- 📚 The video script uses a simulation to visually demonstrate how gravitational potential changes with distance and the effect of mass on the potential well.
- 🎯 Understanding the relationship between gravitational potential, potential energy, and the motion of objects is fundamental to the study of classical mechanics and astronomy.
Q & A
What is the significance of the background picture with the blue sphere in the video?
-The background picture with the blue sphere symbolizes a mass experiencing gravitational force. It is used as an analogy to explain the concept of gravitational potential energy and how an object (like the blue sphere) would move towards a gravitational well if released, illustrating the fundamental ideas discussed in the video.
What is Gravitational Potential Energy (GPE)?
-Gravitational Potential Energy (GPE) is the energy an object possesses due to its position in a gravitational field. It is defined as the work done to bring a mass from infinity to a specific point within the gravitational field. In mathematical terms, GPE is given by the formula U = -G * (m1 * m2) / r, where G is the gravitational constant, m1 and m2 are the masses involved, and r is the distance between the centers of the two masses.
Why is Gravitational Potential Energy negative?
-Gravitational Potential Energy is negative because the work done to move an object against the gravitational force (to infinity) is considered positive, and by definition, we set the potential energy at infinity to zero. Therefore, as an object moves from infinity to a point within a gravitational field, the change in potential energy is negative, indicating that energy has been expended to overcome the gravitational force.
How is Gravitational Potential different from Gravitational Potential Energy?
-Gravitational Potential is the work done to bring a unit mass from infinity to a point within a gravitational field, whereas Gravitational Potential Energy is the work done for any given mass. Gravitational Potential is a scalar quantity and is dimensionally equivalent to energy per unit mass (joules per kilogram), while Gravitational Potential Energy is an extensive quantity and is measured in joules.
What is the relationship between Gravitational Potential (phi) and Gravitational Potential Energy (U)?
-Gravitational Potential (phi) is the per unit mass counterpart of Gravitational Potential Energy (U). The relationship between them is given by the formula phi = U / m, where m is the mass of the object. Essentially, phi represents the gravitational potential energy per unit mass at a particular point in the gravitational field.
How does the shape of the gravitational potential curve change with the mass of the central object?
-The shape of the gravitational potential curve is a function of the mass of the central object. The greater the mass of the central object, the deeper and steeper the gravitational potential well becomes. This means that objects will experience a stronger gravitational pull and will move towards the center of the well (the central massive object) with greater acceleration.
What happens to the gravitational potential as you move from infinity towards a massive object?
-As you move from infinity towards a massive object, the gravitational potential becomes more negative. This is because the work done to move an object against the gravitational force is considered negative work, and the potential energy is defined as the work done against the field. The potential decreases because the object is moving to a position of lower potential energy, which corresponds to being closer to the massive object.
What is the concept of a gravitational well?
-A gravitational well is a region of space where the gravitational potential is lower than at infinity. It is often depicted as a 'valley' or 'well' in a graphical representation of gravitational potential. Objects in a gravitational well are subject to the gravitational force pulling them towards the center of the well, which is the location of the more massive object creating the field.
How does the gravitational potential change when two massive objects are present?
-When two massive objects are present, their individual gravitational potentials combine to form a resultant potential. The resultant potential is the vector sum of the individual potentials at any given point in space. This can result in a complex potential landscape where the potential may be lower in some areas and higher in others, depending on the relative positions and masses of the two objects.
What is the significance of understanding gravitational potential and potential energy?
-Understanding gravitational potential and potential energy is crucial for predicting the behavior of objects in gravitational fields, such as satellites orbiting planets or planets within a galaxy. It helps in calculating the energy required for space missions, understanding the stability of orbits, and the dynamics of celestial bodies under the influence of gravity.
How can the concept of gravitational potential be used to determine the stability of an orbit?
-The concept of gravitational potential can be used to determine the stability of an orbit by analyzing the potential energy of an object within the gravitational field of a massive body. If the potential energy is at a minimum at a certain orbit, it indicates that the orbit is stable, as the object will naturally move towards this state of lower potential energy. Conversely, if the potential energy increases or is higher at a certain point, the object is likely to move away from that point, suggesting an unstable orbit.
Outlines
🌌 Introduction to Gravitational Potential
The video begins with an analogy of a small blue sphere on a trampoline to introduce the concept of gravitational potential. The presenter aims to explain why the sphere would roll towards the center if released, relating it to the difficulty of waking up in the morning due to sinking into the bed. The goal is to understand the concept of gravitational potential and the related formula GPE, and to learn why gravitational potential is associated with negative values. The video connects this concept to the previous knowledge of gravitational force and work done.
📈 Calculating Gravitational Potential Energy
The second paragraph delves into the mathematical aspect of gravitational potential energy, explaining it as the work done to bring a mass from infinity to a specific point. The presenter uses the analogy of lifting a heavy object to illustrate work done and introduces the concept of negative work done when an object is brought closer. The formula for gravitational potential energy is derived from the force-distance graph, using integration to calculate the area under the curve. The result is a negative value for gravitational potential energy, which is a scalar quantity.
🧮 Deriving the Gravitational Potential Energy Equation
This paragraph focuses on the derivation of the gravitational potential energy equation through integration. The presenter explains the process of integrating the force equation (F = G * m1 * m2 / r^2) with respect to the displacement (dr) from infinity to a point r. The integration yields the formula for gravitational potential energy (U = -G * m1 * m2 / r), highlighting the negative sign's significance. The presenter also connects this to the familiar formula mgh, which is used to calculate the change in potential energy near the Earth's surface.
🌐 Understanding Gravitational Potential
The video then introduces gravitational potential, which is defined as the work done to bring a unit mass from infinity to a point. The presenter explains the difference between gravitational potential energy (per mass) and gravitational potential (for a unit mass). The gravitational potential is given by the formula phi = -G * m / r, where m is the mass of the object experiencing the force, and r is the distance from the source of the gravitational field. The concept is further illustrated with a simulation that shows the change in gravitational potential as an object moves from far to near a massive body.
🪐 Gravitational Potential Wells and Satellite Motion
In the final paragraph, the presenter discusses the concept of gravitational potential wells and how they affect the motion of objects like satellites. The video uses a simulation to demonstrate how the gravitational potential changes with distance from a massive object, becoming more negative as the distance decreases. The presenter also explores the effects of changing the mass of the objects in the simulation, showing how the depth of the potential well affects the motion of the smaller object. The concept of balance within the potential well is introduced, explaining how an object can remain stationary at certain points due to equal forces acting in opposite directions.
Mindmap
Keywords
💡Gravitational potential energy (GPE)
💡Gravitational potential
💡Work done
💡Infinity
💡Negative energy
💡Integration
💡Force graph
💡mgh (Mechanical energy at Earth's surface)
💡Unit mass
💡Simulation
Highlights
The concept of gravitational potential energy is introduced as the work done to bring a mass from infinity to a point.
The Earth's gravitational field is used as an example to explain the change in energy when an object is lifted.
Gravitational potential energy is calculated as negative work done, which is the energy change when bringing something from far away to a closer point.
The formula for gravitational potential energy, U = -G * (Mm) / r, is derived from the force equation F = G * (Mm) / r^2.
The unit for gravitational potential energy is Joules, and it is a scalar quantity, not a vector.
Gravitational potential is defined as the work done to bring a unit mass from infinity to a point, using the symbol phi (Φ).
The gravitational potential at a point is given by the equation Φ = -G * M / r, which is the work done per unit mass.
The gravitational potential becomes more negative as the distance decreases, representing a 'well' or 'sink' where objects tend to move towards lower potential values.
The concept of gravitational potential wells is explained, where objects naturally move towards areas of lower potential.
The video includes a simulation demonstrating how gravitational potential changes as an object moves closer to a massive body.
The reason for gravitational potential being negative is explained, relating to the definition of zero potential at infinity and the attractive nature of gravity.
The video discusses the practical application of gravitational potential in understanding the behavior of objects in gravitational fields.
The concept of potential energy is related to the work done against gravity when lifting an object, which is positive work.
The difference between gravitational potential energy (GPE) and gravitational potential is clarified, with GPE being the work done for a specific mass while potential is per unit mass.
The video provides a visual representation of gravitational potential as a 3D surface, illustrating the concept of a potential well.
The importance of understanding gravitational potential and potential energy is emphasized for future studies in physics.
Transcripts
Browse More Related Video
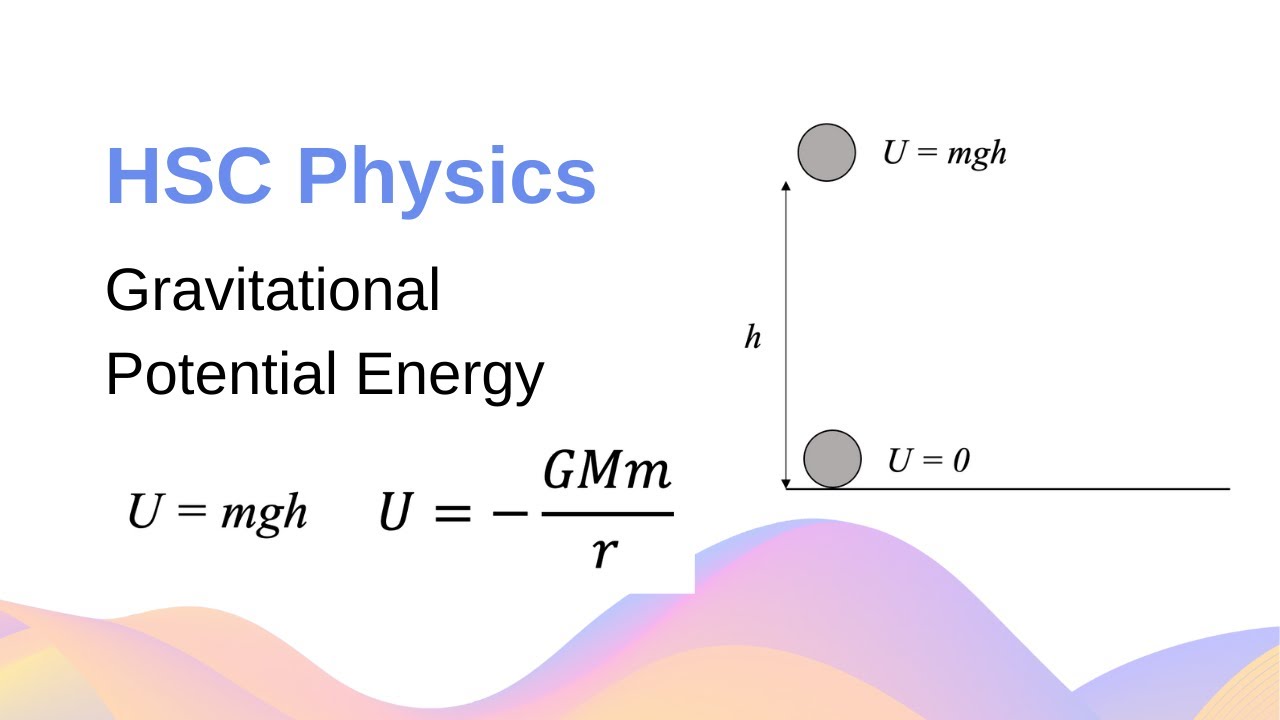
Gravitational Potential Energy & Work Done + Calculation Example // HSC Physics
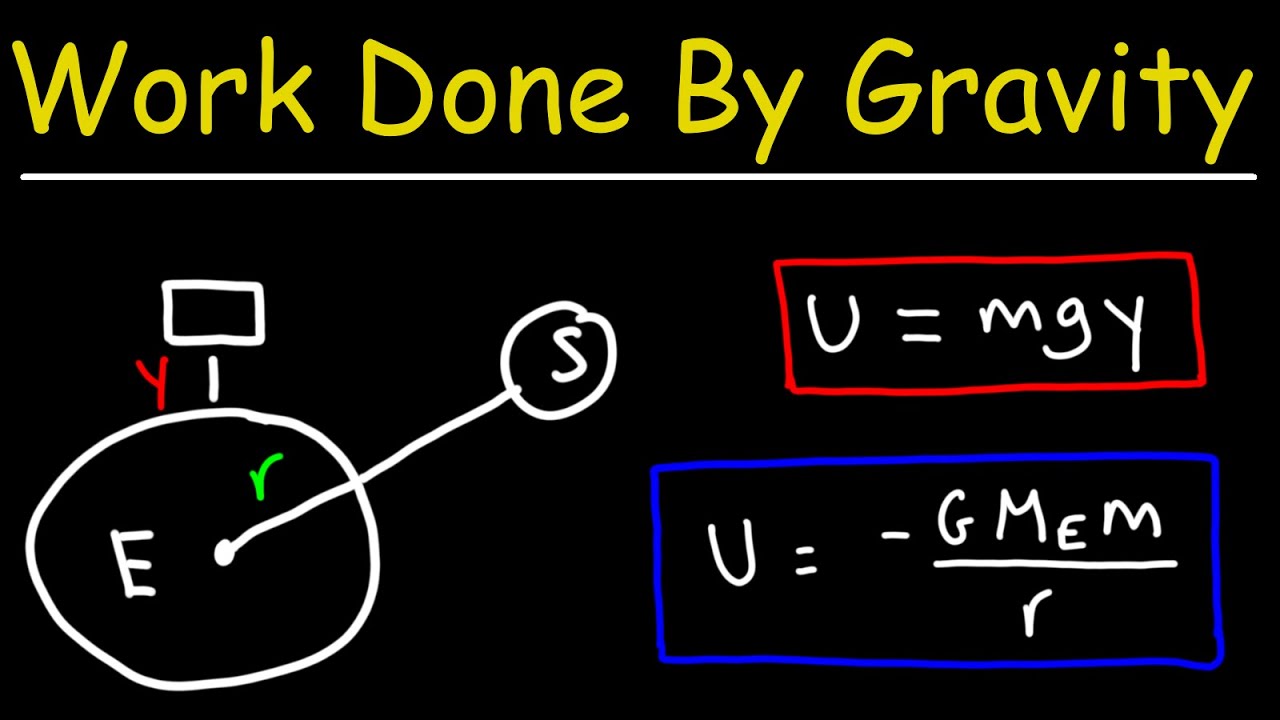
Work Done By Gravity and Gravitational Potential Energy - Physics

Deriving The Formula For Gravitational Potential Energy
13.3b Ex1 MJ20 P42 Q1 Rock Potential Energy | A2 Gravitational Fields | Cambridge A Level Physics

Gravitational Potential Questions | A Level Physics | Formulas, Key Words, Graphs

Gravitational Potential Energy Calculations (GPE) - Mass x Gravity x Height OR GPE=mgh
5.0 / 5 (0 votes)
Thanks for rating: