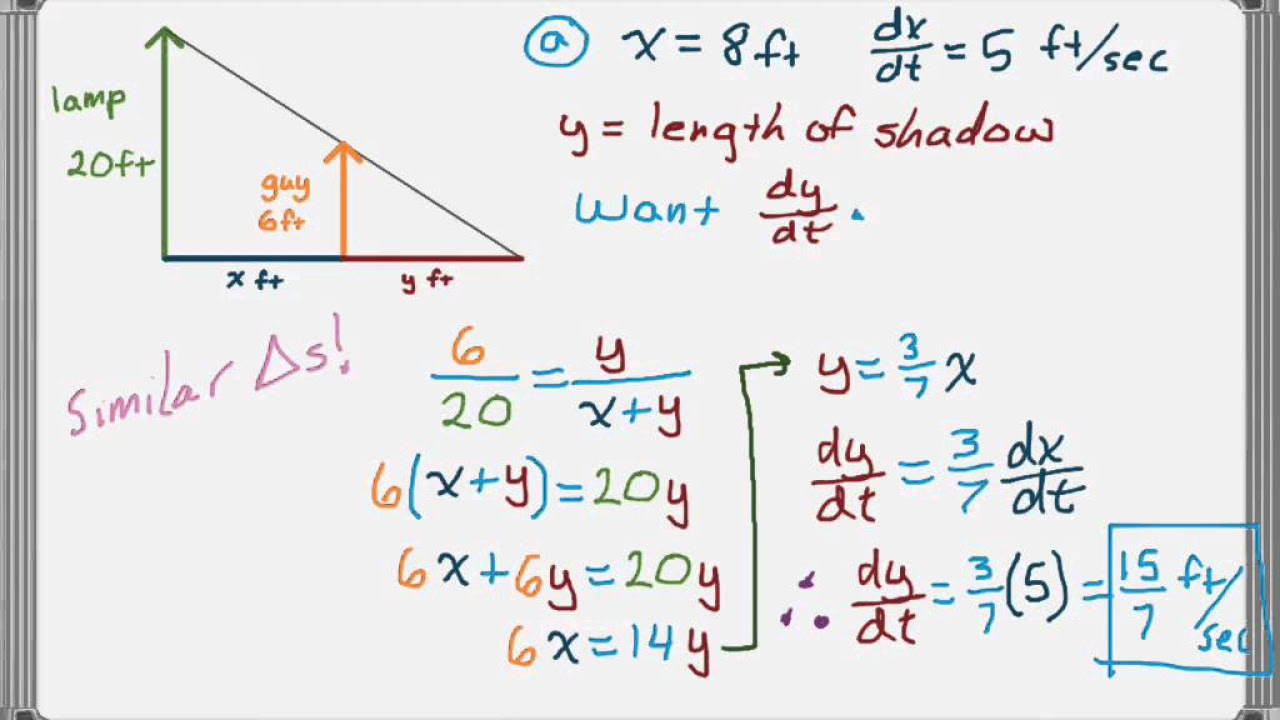Calculus Related Rates - The Shadow Problem
TLDRThe video script presents a related rate problem involving a 15-foot tall streetlight, a 6-foot tall man, and the dynamics of his shadow as he walks away from the light post. The man moves at a speed of 5 feet per second, and the challenge is to determine the speed at which the tip of his shadow moves when he is 40 feet away from the pole. By using the principles of similar triangles and derivatives, the video guides the viewer through the mathematical process to solve for the rate of change of the shadow's tip, ultimately revealing it to be 25/3 feet per second.
Takeaways
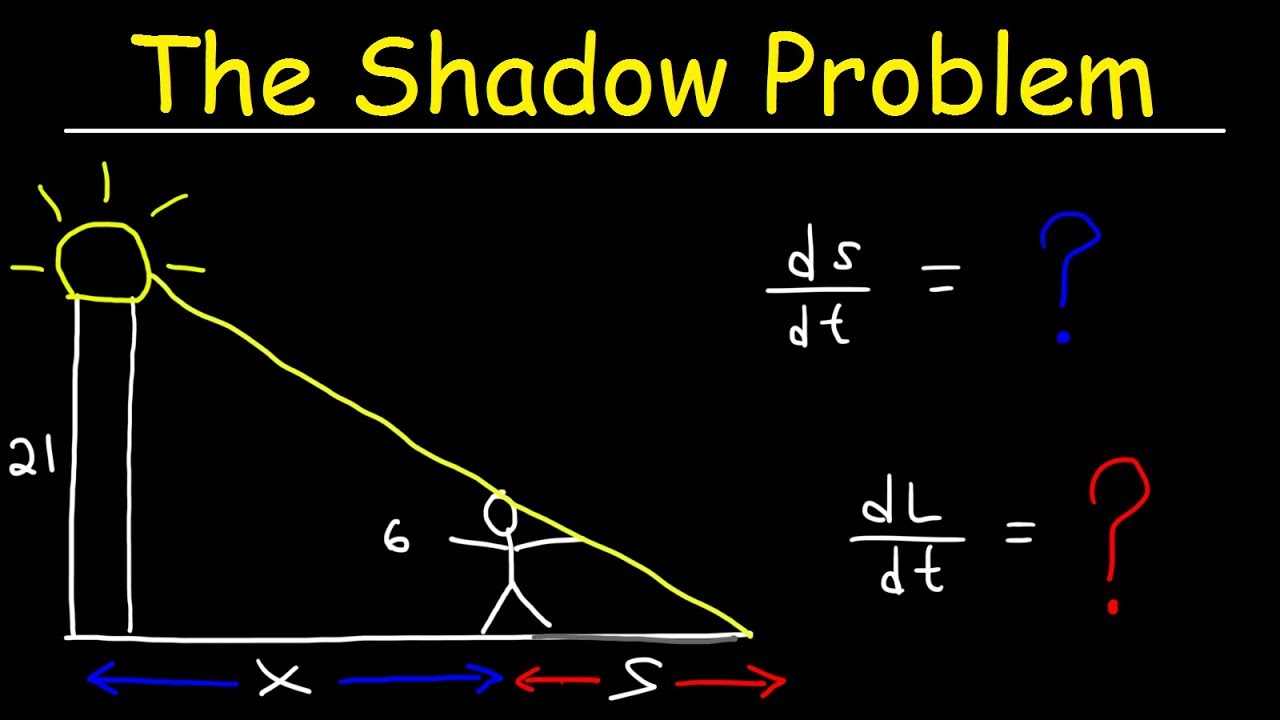
- 📐 The problem involves a 15-foot tall street light, a 6-foot tall man, and the man's moving shadow.
- 🚶♂️ The man walks away from the pole at a speed of 5 feet per second along a straight path.
- 📐 The question asks for the speed of the tip of the shadow when the man is 40 feet from the pole.
- 🎨 A visual representation is suggested to help understand the problem, labeling the distances and angles involved.
- 🔢 The distance from the man to the street light is denoted as X, and the length of the shadow as Y.
- 📐 The rate of change of X with respect to time (dx/dt) is given as 5 feet per second.
- 📐 The problem requires finding the rate of change of Y (dy/dt), but this information is not directly provided.
- 🔄 The solution involves recognizing the similarity of the triangles formed by the street light, man, and shadow.
- 📐 Using the proportionality of the similar triangles, the length of the shadow is expressed as 2/3 times the distance X.
- 🔢 The derivative of the shadow's tip's position with respect to time is calculated as (5/3) * dx/dt.
- 🏁 The final answer is 25/3 feet per second, which is the speed of the tip of the shadow when the man is 40 feet away from the pole.
Q & A
What is the height of the street light mounted on the pole?
-The height of the street light mounted on the pole is 15 feet.
What is the walking speed of the man?
-The man is walking away from the pole at a speed of 5 feet per second.
How far is the man from the pole when the problem is set?
-The man is 40 feet away from the pole when the problem is set.
What is the height of the man?
-The man is 6 feet tall.
What is the main problem we are trying to solve?
-The main problem is to find out how fast the tip of the man's shadow is moving when he is 40 feet away from the pole.
How is the distance X defined in the problem?
-The distance X is defined as the distance from the point where the man's shadow touches the ground to the base of the street light.
How is the distance Y related to the height of the man and the distance X?
-The distance Y, which is the length of the shadow, can be found using the proportionality from the similar triangles formed by the man's height and the distance X, resulting in Y being equal to (2/3)X.
What is the derivative of X with respect to time (T)?
-The derivative of X with respect to time (T), denoted as dX/dt, is 5 feet per second, which represents the man's walking speed.
How do we find the rate of change of the shadow's tip position?
-We find the rate of change of the shadow's tip position by taking the derivative of the total distance (X + Y) with respect to time (T) and then substituting the known values and the relationship between X and Y.
What is the final calculation for the rate of change of the shadow's tip position?
-The final calculation for the rate of change of the shadow's tip position is (5/3) times the derivative of X with respect to time (T), which is (5/3) * 5 feet per second, resulting in 25/3 feet per second.
How can the information from this problem be applied in real-life scenarios?
-The information from this problem can be applied in real-life scenarios such as calculating the speed of moving shadows for lighting design, understanding the effect of changing distances on the perception of motion, and solving related rate problems in physics and engineering.
Outlines
📏 Solving a Related Rate Problem with Shadow Movement
In this paragraph, the speaker introduces a related rate problem involving a street light, a man, and his moving shadow. The problem states that a 15-foot tall street light is mounted on a pole, and a 6-foot tall man walks away from the pole at a speed of 5 feet per second. The challenge is to determine the speed at which the tip of the man's shadow moves when he is 40 feet away from the pole. The speaker suggests drawing a picture to visualize the problem and labels the distances involved. The speaker then sets up the equation for the changing distance (X and Y) and explains that the goal is to find the rate of change of the shadow's tip as the man moves away from the light source.
🔢 Using Similar Triangles to Find the Shadow's Movement Rate
In this paragraph, the speaker continues to work through the related rate problem by using the concept of similar triangles. The speaker identifies two right triangles formed by the street light, the man, and his shadow. By setting up a proportion based on the heights given (15 feet for the street light and 6 feet for the man), the speaker is able to express the length of the shadow (Y) in terms of the distance the man has walked (X). The equation derived is Y = (2/3)X. With this relationship, the speaker then rewrites the expression for the rate of change of (X + Y) entirely in terms of X. By substituting the known rate of change of X (5 feet per second) into the new expression, the speaker calculates the rate of change of the shadow's tip as 25/3 feet per second, providing the solution to the problem.
Mindmap
Keywords
💡related rate problem
💡street light
💡shadow
💡height
💡walking speed
💡distance
💡derivative
💡similar triangles
💡rate of change
💡calculation
💡geometry
Highlights
Introduction to a related rate problem involving a street light, a man, and his shadow.
The street light is mounted at the top of a 15-foot tall pole.
A man who is 6 feet tall walks away from the pole along a straight path.
The man walks at a speed of 5 feet per second.
The problem asks for the speed at which the tip of the man's shadow is moving when he is 40 feet from the pole.
A visual representation is suggested to solve the problem, by drawing a picture of the scenario.
The triangle formed by the street light, the man, and the tip of the shadow is used to find the relationship between the distances.
The problem is approached by finding the rate of change of the sum of distances X and Y with respect to time.
The rate of change of X (DX/DT) is given as 5 feet per second.
The challenge is to find the rate of change of Y (DY/DT) to solve for the shadow's tip movement speed.
The solution involves recognizing the similarity of the triangles formed and setting up a proportion to solve for Y in terms of X.
The derived formula for Y in terms of X is Y = (2/3)X.
The derivative of the sum of X and Y with respect to time T is calculated using the found relationship.
The final calculation shows that the tip of the shadow moves at a speed of 25/3 feet per second.
The problem-solving approach is explained in a step-by-step manner, making it easy to follow and understand.
The video aims to educate viewers on solving related rate problems using geometric relationships and derivatives.
The solution is presented in a clear and concise manner, highlighting the logical steps taken to arrive at the answer.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: