Related Rates - The Shadow Problem
TLDRThis video script presents a mathematical problem involving related rates, specifically the 'shadow problem'. It involves a six-foot man walking away from a 21-foot street light at a rate of 3 feet per second. The lesson explains how to set up and solve the problem using similar triangles and implicit differentiation to find the rate of change of the shadow's length (ds/dt) and the rate at which the tip of the shadow moves (dl/dt). The problem is solved in two parts: first, when the man is 8 feet from the light, and then when he is 10 feet away, resulting in the rates of 6/5 feet per second and 4.2 feet per second, respectively.
Takeaways
- 📚 The lesson focuses on solving the 'shadow problem' within the context of related rates.
- 🚶 A six-foot tall man walks away from a 21-foot tall street light at a speed of 3 feet per second.
- 📐 The problem involves drawing a diagram to visualize the scenario and identify the variables: x (distance from light to man), s (length of shadow), and l (combined height of man and shadow).
- 🔍 Similar triangles are used to set up a proportion between the height of the street light and the length of the shadow, and the height of the man and his shadow.
- 🧐 The key to solving the problem is understanding the relationship between the angles in the triangles and setting up the correct proportion.
- 📝 The equation 15s = 6x + 6s is derived from the proportion, which is then simplified to 15s = 6x.
- 🌟 Implicit differentiation is applied to the equation to find the rate of change of the shadow's length (ds/dt) with respect to time.
- 🏃 The man's walking speed (3 feet per second) is used to determine the rate of change of x (dx/dt), which is crucial for solving for ds/dt.
- 📊 For part b, the rate of change of the shadow's tip (dl/dt) is calculated by differentiating the modified proportion involving the total length l.
- 🔢 The final answers are: ds/dt = 6/5 feet per second (the rate at which the shadow's length changes) and dl/dt = 4.2 feet per second (the rate at which the shadow's tip moves when the man is 10 feet from the light).
- 🎓 The lesson emphasizes the importance of understanding the concepts of related rates and the application of derivatives in practical problems.
Q & A
What is the main topic of the lesson?
-The main topic of the lesson is the shadow problem in related rates.
What are the dimensions of the street light and the man in the problem?
-The street light is 21 feet tall and the man is 6 feet tall.
What is the rate at which the man is walking away from the street light?
-The man is walking away from the street light at a rate of three feet per second.
What do x and s represent in the problem?
-In the problem, x represents the distance between the man and the light, and s represents the length of the shadow.
How are the two triangles in the problem similar?
-The two triangles are similar because they both have the same angle theta and are both right triangles.
What is the equation derived from the proportion of the two similar triangles?
-The equation derived from the proportion is 15s = 6x.
What is the value of ds/dt when the man is 8 feet from the light?
-When the man is 8 feet from the light, ds/dt is 6/5 feet per second.
What is the rate at which the tip of the shadow is moving when the man is 10 feet from the light?
-When the man is 10 feet from the light, the tip of the shadow is moving at a rate of 4.2 feet per second.
How does the man's direction affect the value of dx/dt?
-If the man is walking away from the street light, dx/dt is positive three feet per second. If he were walking towards the light, dx/dt would be negative three feet per second.
What is the significance of the final answers for the rate of shadow length change and the tip of the shadow movement?
-The final answers provide the rates of change for the shadow's length and the tip of the shadow's position. These values help in understanding the dynamics of the shadow as the man moves away from the street light.
How can the equation 15s = 6x be used to find the rate of change of the shadow's tip position?
-By differentiating the equation with respect to time and substituting the known values, we can find the rate of change of the shadow's tip position, represented as dl/dt.
Outlines
🚶♂️ Introduction to the Shadow Problem
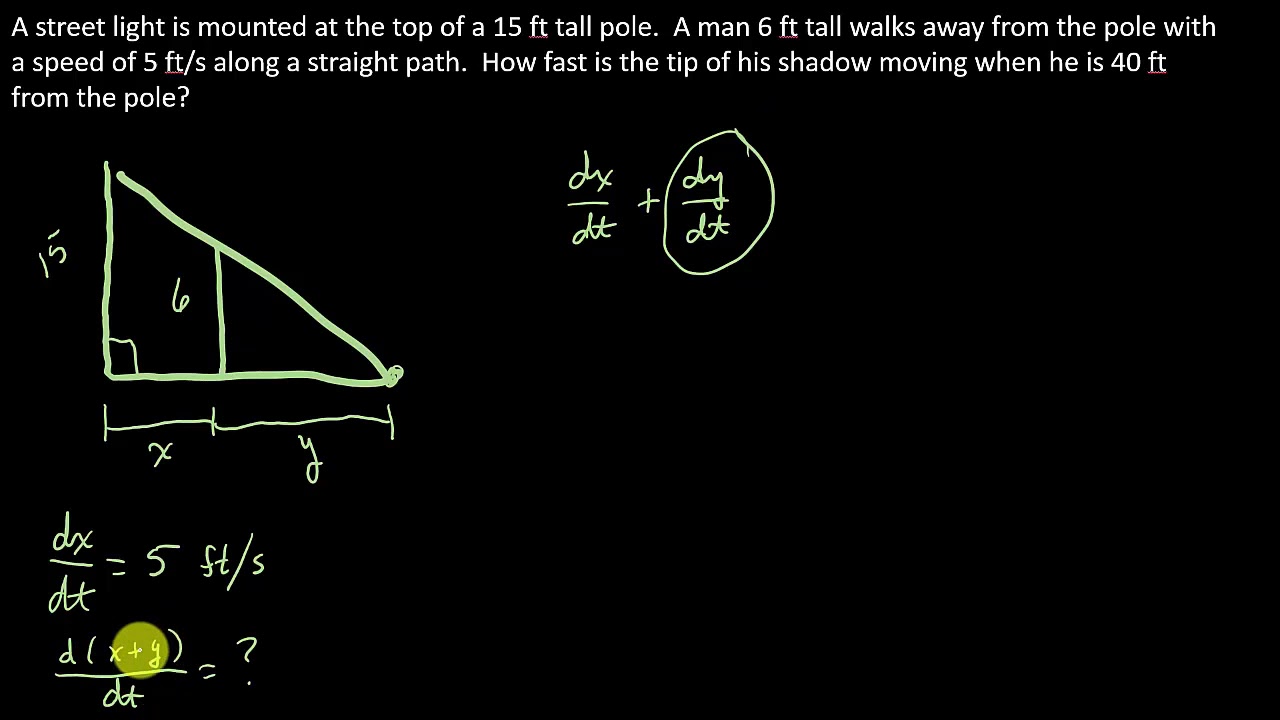
This paragraph introduces the shadow problem in the context of related rates. It describes a scenario where a six-foot-tall man walks away from a 21-foot-tall street light at a speed of three feet per second. The objective is to determine the rate of change of the length of the shadow (ds/dt) when the man is eight feet away from the light. The paragraph emphasizes the importance of understanding the difference between the rate of change of the shadow's length (ds/dt) and the rate of movement of the shadow's tip (dl/dt). It sets the stage for using similar triangles and trigonometric functions to solve the problem, highlighting the need to draw and analyze the triangles formed by the light, the man, and the shadow.
📐 Solving for ds/dt Using Similar Triangles
In this paragraph, the focus is on solving for the rate of change of the shadow's length (ds/dt) using the concept of similar triangles. The explanation begins with setting up a proportion between the large triangle formed by the street light, the man, and the shadow, and the smaller triangle formed just by the man and his shadow. By equating the tangent of the angles in both triangles, an equation relating the height of the light (21 feet), the distance between the man and the light (x), and the length of the shadow (s) is derived. The paragraph then details the process of implicit differentiation to find ds/dt, emphasizing the need to account for dx/dt, the rate at which the man is moving away from the light. The final answer for ds/dt when the man is eight feet from the light is calculated to be 6/5 or 1.2 feet per second.
🏃♂️ Calculating dl/dt When 10 Feet from the Light
The final paragraph addresses the second part of the problem, which is to find the rate at which the tip of the shadow is moving (dl/dt) when the man is 10 feet from the light. To achieve this, the paragraph revisits the earlier derived equation and replaces x + s with l, the total height of the triangle. By cross-multiplying and differentiating both sides with respect to time, the expression for ds/dt is substituted to solve for dl/dt. The paragraph concludes by simplifying the equation to find that dl/dt is 4.2 feet per second when the man is 10 feet away from the light. This value represents the rate at which the tip of the shadow moves, providing a complete solution to the shadow problem.
Mindmap
Keywords
💡Shadow Problem
💡Related Rates
💡Street Light
💡Man
💡Similar Triangles
💡Tangent
💡Implicit Differentiation
💡Derivative
💡Rate of Change
💡Distance
💡Proportion
Highlights
The lesson focuses on the shadow problem in related rates, involving a six-foot man walking away from a 21-foot tall street light at a rate of three feet per second.
A diagram is used to visualize the scenario, with the man, street light, and the shadow formed behind the person.
The distance between the man and the light is denoted as x, and the length of the shadow as s, with l representing the sum of x and s.
The problem asks for the rate of change of the shadow's length (ds/dt) when the man is eight feet from the light.
Part B of the problem seeks the rate at which the tip of the shadow is moving when the man is ten feet from the light, which is equivalent to the rate of change of l (dl/dt).
To calculate ds/dt, the lesson introduces the concept of drawing similar triangles and setting up a proportion between them based on their shared angle theta.
The proportion derived from the similar triangles is 21 over (x + s) equals 6 over s, which is then used to find the relationship between x and s.
Implicit differentiation is performed on the equation to find the derivative with respect to time, resulting in 15s = 6x.
The man's walking speed is used to determine dx/dt, which is positive three feet per second as he moves away from the street light.
By substituting dx/dt into the equation, the value of ds/dt is calculated to be six over five feet per second.
For Part B, the rate of the tip of the shadow's movement (dl/dt) is found by differentiating the modified proportion involving l.
The final answer for Part B is dl/dt equals 4.2 feet per second, indicating the rate at which the tip of the shadow moves when the man is ten feet from the light.
The lesson emphasizes the importance of understanding the difference between ds/dt and dl/dt, as they represent different aspects of the shadow's change.
The problem-solving approach involves a combination of geometry, algebra, and calculus, showcasing the integration of mathematical concepts.
The lesson demonstrates the practical application of related rates in real-world scenarios, such as the movement of shadows.
The use of similar triangles is a key method for solving this problem, highlighting the importance of recognizing and applying geometric relationships.
The lesson provides a step-by-step guide to solving the problem, making it accessible to learners with varying levels of mathematical background.
The problem requires the application of the constant multiple rule in calculus, demonstrating the utility of this rule in related rate problems.
The lesson concludes with a clear and concise summary of the solution, reinforcing the key concepts and methods used.
Transcripts
Browse More Related Video
Calculus Related Rates - The Shadow Problem
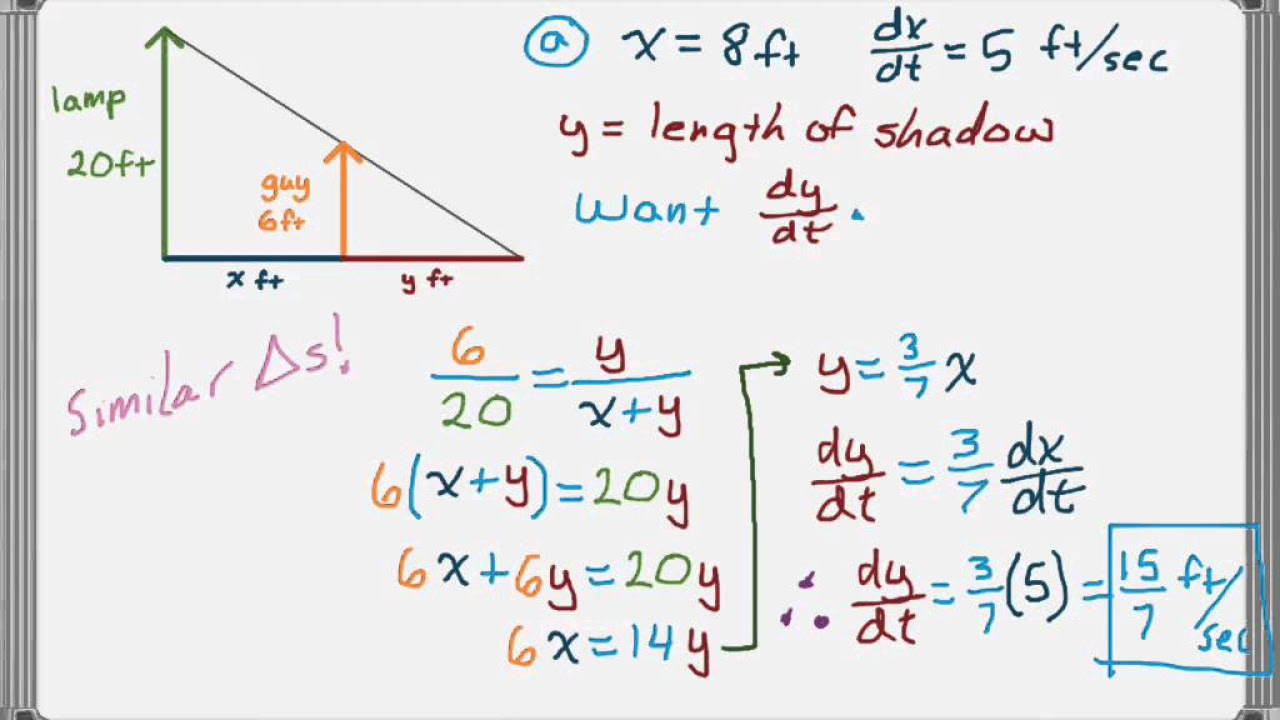
Related Rates - The Shadow Problem

Solving a falling ladder problem using related rates

How to solve a changing area of circle with related rates
Moving Shadow Problem (Related Rates)

Related rates: shadow | Applications of derivatives | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: