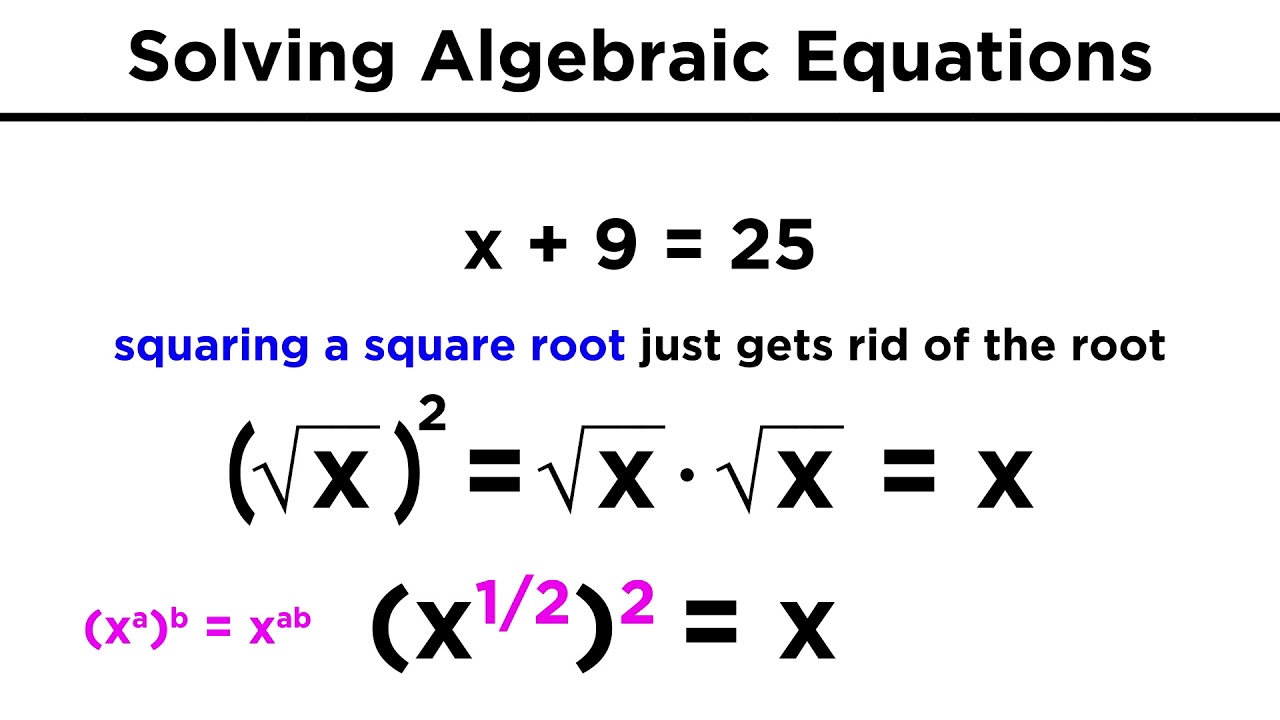Square Roots, Cube Roots, and Other Roots

Professor Dave Explains
11 Sept 201709:02
EducationalLearning
32 Likes 10 Comments

TLDRThe script explains the concept of square roots in algebra, describing how to solve equations with square roots and explaining that square roots of positive numbers have two possible solutions. It compares properties of square roots to cube roots and other roots. The script states that roots represent fractional exponents; for example, a square root represents an exponent of 1/2. It shows how to simplify radical expressions with fractional exponents. The video aims to provide a foundational understanding of roots to prepare for more advanced algebra concepts.

Takeaways
  • 📊 The inverse operation to squaring a number is taking the square root, which helps solve equations like X squared equals a number.
  • 📖 Square roots result in two answers for positive numbers, representing both the positive and negative roots, except in specific cases like the square root of negative numbers, which are not real.
  • 📈 Perfect squares have easy-to-remember square roots, and it's useful to memorize the first ten or twenty to simplify calculations.
  • 📝 Radical expressions involving square roots can sometimes be simplified by identifying and extracting the square root of perfect square factors.
  • 🤖 Cube roots differ from square roots in that they can apply to negative numbers and yield a single unique result.
  • 💡 The nature of the root (odd or even) affects whether negative numbers can be used and how many real solutions exist.
  • 📉 Roots represent fractional exponents, with the square root being equivalent to raising a number to the one-half power.
  • 🔨 Operations with roots and exponents can be combined and simplified using rules of exponents and fractions to manage more complex expressions.
  • 📄 Understanding roots and their properties, including how to simplify and manipulate them, is fundamental in algebra and higher mathematics.
  • 🚀 The comprehension of fractional exponents as a combination of powers and roots enriches the toolkit for solving a wide range of mathematical problems.
Q & A

  • What is the inverse operation of squaring something?

    -The inverse operation of squaring something is taking the square root. For example, if x^2 = 9, then the square root of 9 is x.

  • Why are there two solutions when taking the square root of a positive number?

    -When taking the square root of a positive number, there are two solutions - a positive and negative value - because squaring either the positive or negative value will result in the original positive number. For example, the square root of 9 is ±3, since (3)^2 = 9 and (-3)^2 = 9.

  • Can you take the square root of negative numbers?

    -No, you cannot take the square root of negative numbers and get a real solution. Attempting to do so results in an imaginary number. Only positive numbers have real square roots.

  • How are radical expressions simplified?

    -Radical expressions can be simplified by factoring out perfect squares. For example, √8 can be simplified to 2√2, since 8 = 4 x 2, and √4 = 2. This allows a simplified radical form.

  • What are the differences between square roots and cube roots?

    -Square roots of positive numbers have two real solutions, while cube roots have only one real solution. Also, you can take the cube root of negative numbers, but not the square root. Cube roots follow rules similar to other odd roots.

  • How are roots related to fractional exponents?

    -Roots represent fractional exponents. For example, the square root is the same as raising a value to the 1/2 power. This generalizes, so the cube root is the 1/3 power, fourth root is 1/4 power, etc.

  • What does it mean to raise a number to a fractional exponent?

    -Raising a number x to a/b power means to raise x to the a power first, and then take the b root. For example, x^(2/3) means square x first and then take the cube root.

  • How can you simplify a complex root expression?

    -Convert all roots to fractional exponents, simplify any numerical exponents using the rules of exponents, then convert back to root notation. This allows simplification through exponent arithmetic.

  • What are some examples of perfect squares?

    -Some perfect squares are 4, 9, 16, 25, 36 and so on. Perfect squares have integer square roots, so they can be useful to memorize for simplifying radicals.

  • What are irrational numbers?

    -Irrational numbers are real numbers that cannot be expressed as a simple fraction. Some square roots are irrational numbers, meaning the root continues forever as a non-repeating decimal.

Outlines
00:00
📚 Understanding Square Roots

Professor Dave introduces the concept of square roots as the inverse operation of squaring numbers. The tutorial begins with basic algebraic manipulations, leading to the explanation that taking the square root of a number answers the question of what number, multiplied by itself, yields the original number. A significant emphasis is placed on the fact that both positive and negative numbers can have square roots, illustrated by the example of the square root of nine being both positive and negative three. The video explains that while perfect squares have easy-to-find square roots, other numbers may result in irrational square roots, extending to the discussion on radical expressions and the simplification of square roots of non-perfect squares, like root eight simplifying to plus or minus two root two.

05:00
🔢 Exploring Roots Beyond Squares

This section delves into cube roots and higher-order roots, explaining their unique properties. For example, cube roots can be taken of negative numbers, and each number has only one unique cube root, contrasting with square roots which can have two (positive and negative). The pattern of roots is explored, noting that odd roots allow for negative numbers while even roots do not. Professor Dave then transitions to the concept of fractional exponents, illustrating how roots can be represented as raising a number to a fractional power. This segment clarifies operations with exponents through examples, such as simplifying expressions by converting roots into fractional exponents and combining operations into one fraction, culminating in a practical application of these principles to simplify a complex expression.

Mindmap
Keywords
💡Square root
The square root of a number is a value that, when multiplied by itself, produces the original number. For example, the square root of 9 is 3, because 3 x 3 = 9. Square roots are the inverse operation of squaring a number. They are represented by the radical symbol √. In the video, square roots are introduced as the method to solve equations involving squared variables, like x^2 = 9.
💡Perfect square
A perfect square is an integer that is the square of another integer. For example, 4, 9, 16 are perfect squares since they are the squares of 2, 3, and 4 respectively. Perfect squares have tidy square root values that are also integers. The video emphasizes memorizing perfect squares since their roots are easy to determine.
💡Irrational number
An irrational number is a real number that cannot be represented as a simple fraction. Many square roots of non-perfect squares are irrational numbers, meaning their decimal values go on forever without repeating. This makes their exact values impossible to write out. The video introduces irrational numbers as an interesting consequence of taking square roots.
💡Radical expression
A radical expression contains a radical symbol representing a root operation. For example √8, √27 are radical expressions involving square roots. The video discusses simplifying radical expressions by factoring integers under the radical into perfect squares.
💡Cube root
The cube root of a number is the value that must be cubed (raised to the 3rd power) to produce the original number. It is represented by the radical ∛. Cube roots differ from square roots in that negatives can have real cube roots, and there is only one real cube root value for any given number.
💡Fractional exponent
A fractional exponent represents a root operation, where the denominator is the index of the root. For example, x^(1/2) represents the square root of x. This allows roots to be combined and manipulated using exponent rules. The video emphasizes this as a key insight about roots.
💡Odd root
An odd root is a root with an odd index, like the cube root or 5th root. Odd roots have similar properties to cube roots in that there is only one real value for the odd root of a number. The video contrasts odd and even roots.
💡Even root
An even root is a root with an even index, like the square root or 4th root. Even roots have similar properties to square roots in that there are two possible real values for the even root of a positive number. The video contrasts odd and even roots.
💡Simplifying radicals
Simplifying radicals means rewriting them in an equivalent form but with smaller radicands and coefficients. This is done by factoring integers under the radical symbol and pulling out perfect square factors. The video demonstrates simplifying radicals like √8 and √27.
💡Negative number square roots
The video emphasizes that only non-negative real numbers have real square roots. Trying to take the square root of a negative number results in an imaginary number, which cannot be expressed on the real number line. This is an important limitation of square roots.
Highlights

Discussion of using machine learning models to analyze medical images for diagnosis

Explanation of convolutional neural networks and how they are applied to image classification

Overview of training deep learning models on large labeled datasets to recognize patterns in images

Description of using segmentation models to identify different structures in medical scans

Discussion of how AI can help radiologists analyze images more efficiently and accurately

Explanation of challenges in applying AI to medical imaging, like lack of curated training data

Examples of how AI is being used in products for automated detection of abnormalities in X-rays and scans

Overview of research on using AI to predict disease risk and progression from medical images

Discussion of regulatory requirements for getting AI imaging products approved for clinical use

Description of privacy concerns around use of patient imaging data for training models

Examples of open source datasets that can be used to benchmark AI imaging algorithms

Overview of multimodal models that combine imaging with other data like genetics for diagnosis

Discussion of how AI could improve early detection and precision diagnosis in the future

Description of limitations of current AI techniques and need for advances in computer vision

Conclusion that AI holds promise to transform medical imaging but still requires ongoing research

Transcripts

Browse More Related Video

Solving Algebraic Equations With Roots and Exponents

Square roots explained Bob Ross style

Complex Numbers: Operations, Complex Conjugates, and the Linear Factorization Theorem

Algebra Basics: Exponents In Algebra - Math Antics

Fundamental Theorem of Calculus Part 2

How to Use Your Scientific Calculator

Rate This

5.0 / 5 (0 votes)

Thanks for rating: