Related Rates - The Shadow Problem

turksvids
2 May 201305:57
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a classic shadow problem involving a person walking away from a lamp post. It introduces two main questions: the rate at which the length of the person's shadow grows and the rate at which the tip of the shadow moves across the ground. The first question is solved using the concept of similar triangles, deriving that the rate of shadow growth is independent of the person's distance from the lamp and is calculated to be 15/7 feet per second when the person is 8 feet away from the lamp. The second question involves finding the rate at which the tip of the shadow moves away from the lamp post, which is determined by adding the rate of the person's movement (5 feet per second) to the previously calculated rate of shadow growth (15/7 feet per second), resulting in a total of 50/7 feet per second. The script offers two methods for solving the problem, emphasizing the importance of recognizing similar triangles and the ingenuity required for the alternative method.

Takeaways
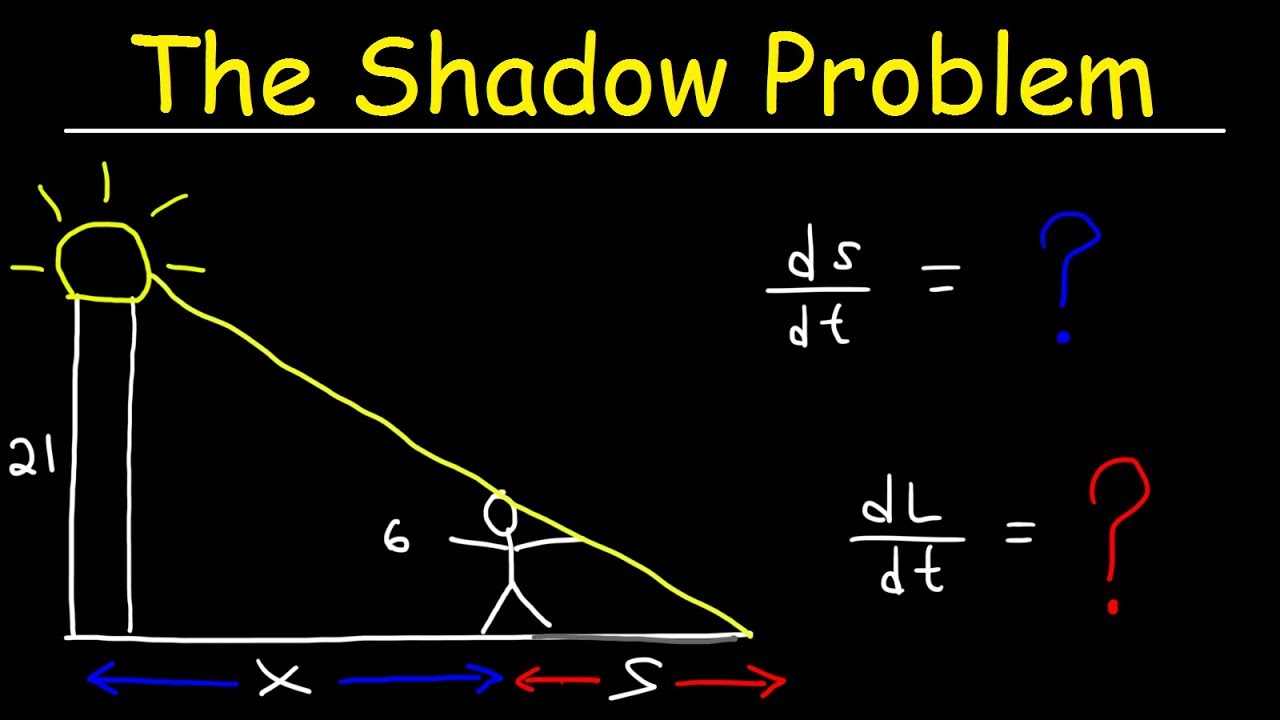
  • 📏 The problem involves a man walking away from a lamp post, with the lamp being 20 feet tall and the man being 6 feet tall.
  • 🚶‍♂️ The man walks away from the lamp at a rate of 5 feet per second, and we are interested in the rate of change of his shadow's length and the tip of the shadow's movement.
  • 🔲 The solution to the first question uses similar triangles to relate the height of the lamp to the height of the man and the length of the shadow.
  • 🔄 The rate at which the length of the shadow increases (dy/dt) is independent of the current distance (x) from the lamp.
  • 🧮 By setting up the ratio of the similar triangles, we find that dy/dt equals 3/7 of dx/dt, which is given as 5 feet per second, resulting in a shadow length increase rate of 15/7 feet per second.
  • 📐 An alternative method involves drawing a perpendicular line from the man's head to establish additional similar triangles, which simplifies the algebraic process.
  • 🤔 The second part of the problem asks for the rate at which the tip of the shadow moves across the ground, which is different from the rate of the shadow's length increasing.
  • 🌡 The distance from the base of the lamp to the tip of the shadow is represented as (x + y), and its rate of change with respect to time involves both dx/dt and dy/dt.
  • 🔄 For part B, the overall rate of change of the tip of the shadow's position is the sum of dx/dt and dy/dt, which we've already calculated.
  • 🏁 The final answer for the rate at which the tip of the shadow moves away from the lamp is 50/7 feet per second.
  • 🎓 The problem-solving approach emphasizes the importance of understanding the geometric relationships and applying the concept of similar triangles.
  • 📈 The problem illustrates the application of derivatives in real-world scenarios, specifically in calculating rates of change with respect to time.
Q & A

  • What is the classic shadow problem described in the transcript?

    -The classic shadow problem involves a person walking away from a lamp post at a certain rate, with the goal of finding the rate at which the length of the person's shadow increases and the rate at which the tip of the shadow moves across the ground.

  • What are the given dimensions in the problem?

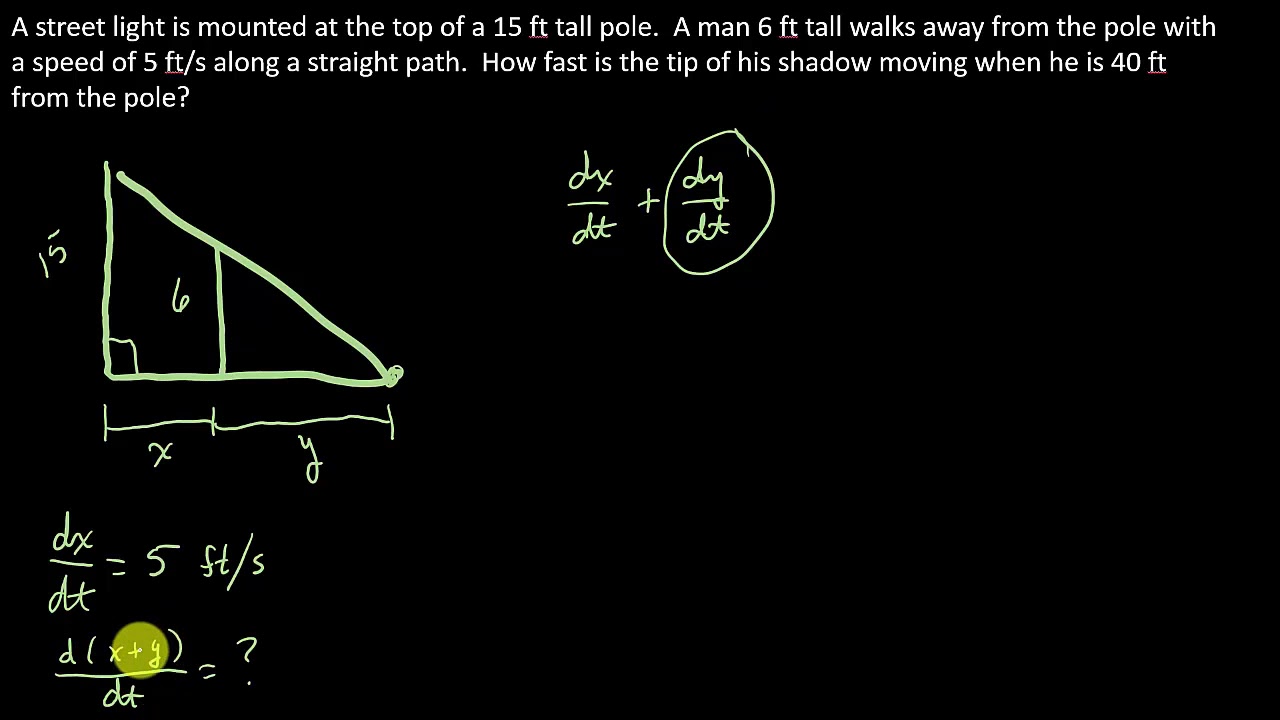
    -The lamp post is given as 20 feet tall, the person is 6 feet tall, and the person walks away from the lamp at a rate of 5 feet per second.

  • At what distance from the lamp post is the rate of the shadow's length increase calculated?

    -The rate of the shadow's length increase is calculated when the person is 8 feet away from the lamp post.

  • What is the relationship between the height of the lamp post, the person, and the length of the shadow?

    -The relationship is based on similar triangles. The height of the person (6 feet) to the height of the lamp post (20 feet) is equivalent to the length of the shadow (Y) to the distance from the lamp post (X plus Y).

  • What is the rate at which the length of the shadow increases when the person is 8 feet from the lamp post?

    -The rate at which the length of the shadow increases is 15/7 feet per second.

  • Why is the rate of the shadow's length increase independent of the current value of X?

    -The rate is independent of the current value of X because the derivative dy/dt, which represents the rate of change, does not involve X directly, showing that the rate of increase is constant regardless of the distance from the lamp post.

  • What is the method used to find the rate at which the tip of the shadow moves across the ground?

    -The method involves taking the derivative with respect to time of the total distance from the base of the lamp to the tip of the shadow, which is X plus Y, and using the previously calculated values of dx/dt and dy/dt.

  • What is the final answer for the rate at which the tip of the shadow moves across the ground?

    -The final answer is 50/7 feet per second.

  • Why is the second part of the problem considered different from the first part?

    -The second part is different because it asks for the rate at which the tip of the shadow moves across the ground, which involves the entire distance from the base of the lamp to the tip of the shadow, not just the length of the shadow itself.

  • What is the significance of the rectangle formed in the second method?

    -The rectangle formed in the second method helps to create two similar triangles by angle-angle similarity, which allows for a simpler ratio setup and quicker calculation of the rate of the shadow's length increase.

  • How does the use of similar triangles simplify the solution to the problem?

    -Using similar triangles allows for the establishment of a ratio between the sides of the triangles, which can be translated into an equation that relates the known values and the unknown rate of change, simplifying the algebraic manipulation needed to find the solution.

  • What is the key takeaway from the problem regarding the relationship between the person's walking speed and the rate of the shadow's length increase?

    -The key takeaway is that the rate of the shadow's length increase is a constant value (15/7 feet per second) and is not directly dependent on the person's walking speed or the current distance from the lamp post.

Outlines
00:00
📏 Solving the Shadow Length Rate Problem

This paragraph introduces a classic problem involving a person walking away from a lamp post, casting a shadow. The problem involves a lamp that is 20 feet tall, a person who is 6 feet tall, and the person walking away at a speed of 5 feet per second. The main task is to find the rate at which the shadow's length increases when the person is 8 feet from the lamp. The solution involves setting up similar triangles and using algebra to find the derivative of the shadow's length with respect to time, which is shown to be 15/7 feet per second, independent of the person's distance from the lamp. An alternative method is also briefly mentioned, which involves drawing a perpendicular line and identifying similar triangles to simplify the algebraic process.

05:05
🏃‍♂️ Calculating the Shadow Tip's Speed

The second paragraph addresses the second part of the problem, which is to find the rate at which the tip of the shadow moves across the ground away from the lamp post. This involves calculating the derivative with respect to time of the distance from the base of the lamp to the tip of the shadow, which is the sum of the person's distance from the lamp (X) and the length of the shadow (Y). Utilizing the previously calculated rate of the shadow's length increase (dy/dt = 15/7 feet per second) and the given speed at which the person walks away (dx/dt = 5 feet per second), the overall rate of the tip of the shadow moving is determined to be 50/7 feet per second. The paragraph concludes with a note of encouragement for solving the problem.

Mindmap
Keywords
💡Shadow Problem
The shadow problem is a classic physics problem that involves calculating the rate of change of a person's shadow as they move away from a lamp post. It is central to the video's theme as it is the main problem being solved. The video discusses two parts to the problem: the rate at which the length of the shadow increases and the rate at which the tip of the shadow moves across the ground.
💡Similar Triangles
Similar triangles are a geometric concept used in the video to solve the shadow problem. They are two triangles that have the same shape but not necessarily the same size. In the context of the video, similar triangles are formed by the lamp post, the person, and their respective shadows, allowing for the application of ratios to find the unknown variables. The script uses similar triangles to establish a relationship between the height of the lamp post, the person, and the length of the shadow.
💡Derivative
The derivative is a fundamental concept in calculus representing the rate at which a quantity changes with respect to another quantity. In the video, derivatives are used to find the rate at which the length of the shadow (dy/dt) and the tip of the shadow (dx/dt + dy/dt) change over time as the person moves away from the lamp post. The calculation of derivatives is a key step in solving the shadow problem.
💡Rate of Change
The rate of change refers to how fast a quantity is changing at a given moment. It is a central concept in the video, as the problem requires finding the rate at which the shadow's length and the tip of the shadow are changing as the person walks away from the lamp post. The rate of change is calculated using derivatives, which are then applied to the given scenario to find the answer.
💡Lamp Post
The lamp post is a key element in the shadow problem discussed in the video. It serves as a fixed reference point from which the person's shadow is cast. The height of the lamp post is given as 20 feet, which is used in the calculations to determine the length of the shadow and the rate at which it changes. The lamp post's role is crucial in setting up the geometry of the problem.
💡Distance
Distance is a measure of how far apart objects are. In the video, the distance is used to describe the separation between the person and the lamp post (X) and the length of the person's shadow (Y). The rate at which these distances change over time is a primary focus of the problem-solving process. The script mentions that the rate of change of the shadow's length is independent of the current value of X, which is a significant insight in the problem.
💡Algebra
Algebra is a branch of mathematics that uses symbols and rules to solve equations. In the video, algebra is used to set up and solve equations based on the geometric relationships between the lamp post, the person, and the shadow. It is through algebraic manipulation that the video derives the expressions for the rates of change (dy/dt and dx/dt + dy/dt).
💡Rectangle
A rectangle is a geometric shape with four right angles. In the video, the concept of a rectangle is used to establish a right-angled figure that helps in setting up similar triangles. The person's height and the distance from the person to the lamp post form one side of a rectangle, which is then used to relate to the length of the shadow (Y) and the distance from the lamp post (X).
💡Perpendicular
Perpendicular refers to a line or plane that forms a right angle with another. In the context of the video, the person and the lamp post are both perpendicular to the ground, and a line is drawn perpendicular from the person's head to the ground to form a right angle. This helps in creating similar triangles and solving the problem using geometric relationships.
💡Conceptual Problem
A conceptual problem is a type of problem that requires understanding the underlying concepts to solve it. The video discusses how some people might confuse the rate at which the length of the shadow increases with the rate at which the tip of the shadow moves across the ground. The video emphasizes the importance of understanding the conceptual differences between these two aspects of the problem.
💡Rate at which the Tip of the Shadow Moves
This refers to the speed at which the end of the shadow moves away from the lamp post as the person walks. It is the second part of the shadow problem discussed in the video. The calculation involves finding the derivative of the total distance from the base of the lamp post to the tip of the shadow with respect to time, which is the sum of the derivatives of the person's distance from the lamp post and the length of the shadow.
Highlights

The problem involves a person walking away from a lamp post, creating a shadow.

The lamp post is 20 feet tall, and the person is 6 feet tall.

The person walks away from the lamp at a rate of 5 feet per second.

Two questions are typically asked: the rate of the shadow's length and the rate at which the tip of the shadow moves.

The rate at which the length of the shadow increases is independent of the distance from the lamp.

Similar triangles are used to solve the problem, with the person's height and the shadow's length forming one triangle, and the lamp's height and the total distance forming another.

The solution involves setting up a ratio of the heights and bases of the triangles and solving for the derivative with respect to time.

The rate of the shadow's length increasing when the person is 8 feet from the lamp is found to be 15/7 feet per second.

An alternative method involves drawing a perpendicular line from the person's head to create additional similar triangles.

This alternative method requires ingenuity and can be faster, though it's less commonly thought of.

For Part B, the focus is on the rate at which the tip of the shadow moves across the ground.

The distance from the base of the lamp to the tip of the shadow is given by X + Y, where X is the distance from the lamp and Y is the shadow's length.

The derivative of X + Y with respect to time is used to find the rate at which the tip of the shadow moves.

The solution to Part A is utilized in Part B to find the overall rate of the shadow's tip movement.

The final answer for the rate at which the tip of the shadow moves is 50/7 feet per second.

The problem-solving approach emphasizes the importance of understanding the underlying geometry and the application of similar triangles.

The transcript provides a clear, step-by-step explanation of the problem, making it accessible to learners.

The presentation includes a review of the problem-solving process, reinforcing the concepts taught.

Transcripts

Browse More Related Video

Related Rates - The Shadow Problem

Calculus Related Rates - The Shadow Problem

Related rates: shadow | Applications of derivatives | AP Calculus AB | Khan Academy

Moving Shadow Problem (Related Rates)

Solving a falling ladder problem using related rates

How to solve a changing area of circle with related rates

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Shadow ProblemGeometryAlgebraRate of ChangeSimilar TrianglesLamp PostProblem SolvingMath PuzzleVisual LearningEducational ContentMathematicsDynamic Systems