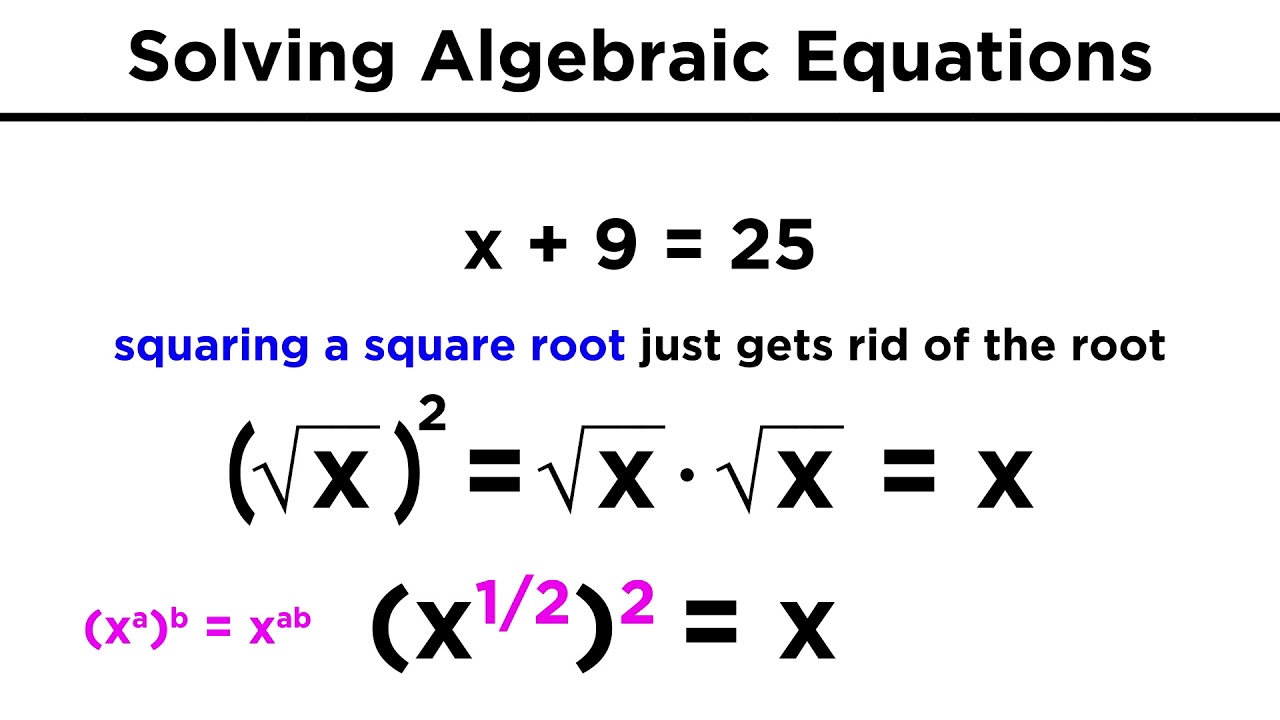Simplifying Expressions With Roots and Exponents
TLDRThe video demonstrates step-by-step techniques for simplifying algebraic expressions containing exponents, radicals, fractions, and roots. Several examples are shown, applying rules like the exponent distribution law, laws for manipulating negative exponents, laws for dividing exponential terms, and extracting roots. The narrator simplifies increasingly complex expressions, explaining his reasoning while emphasizing the importance of going one step at a time. After multiple demonstrations, the narrator concludes that even very complicated expressions can be simplified by methodically applying basic algebraic rules and invites viewers to practice on their own.
Takeaways
- 😀 Exponents distribute over products and quotients, but not sums or differences.
- 😯 To evaluate powers of sums, we need techniques learned later.
- 🤓 To simplify exponents, multiply the exponents when raising powers to powers.
- 🧐 Fractions raised to powers means the numerator and denominator are both affected.
- 🔎 Negative exponents mean to flip the fraction and change the exponent's sign.
- 🤔 To divide powers with the same base, subtract the exponents.
- 😃� Need parentheses when subtracting entire exponent in denominator.
- 😎 Can break down roots to take out perfect square and cube factors.
- 🥳 Simplify roots and exponents step-by-step using known rules.
- 📝 Practice problems check comprehension of simplification rules.
Q & A
What is the difference between 6 X^3 Y squared and 6 X^3 Y^2?
-When we say 'quantity squared', it indicates that the entire quantity inside the parentheses is being squared. On the other hand, 6 X^3 Y^2 implies that only the Y term is being squared.
Why can't we distribute exponents over sums?
-Distributing exponents over sums leads to incorrect results, as shown in the example where (3+2)^2 ≠ 3^2 + 2^2. We can only distribute exponents over products and quotients.
How do we simplify a negative exponent on a fraction?
-To simplify a negative exponent on a fraction, we flip the fraction upside down and change the exponent to positive. For example, X^-2/3 becomes (1/X)^(2/3).
When can we subtract exponents?
-We can only subtract exponents when the base is the same in both terms. For example, A^2x / A^x = A^(2x - x) = A^x. If the bases differ, we cannot subtract the exponents.
How do we simplify roots of numbers that are not perfect squares or cubes?
-If the number under the radical is not a perfect square or cube, we factor it into prime factors and take out factors we can simplify. For example, √32 = √(16 x 2) = 4√2.
What is the first step when simplifying an expression with exponents?
-The first step is to distribute the outermost exponent over everything within parentheses or fractions.
When can we combine like terms under radicals?
-We can only combine like terms under the same radical symbol. For example, we can combine 12X^2√2 + 12X^2√2, but we cannot combine terms with different radicals.
What is the process for simplifying complex expressions step-by-step?
-1. Distribute outermost exponents over parentheses/fractions. 2. Simplify exponents using rules. 3. Take out common factors from radicals. 4. Simplify and combine like terms. 5. Simplify any remaining fractions.
How do we evaluate something raised to a fractional exponent?
-To evaluate a base raised to a fractional exponent, first take the root indicated by the denominator, then raise that result to the power indicated by the numerator.
When does an expression with radicals simplify to zero?
-An expression simplifies to zero when you have the same term with a radical on both sides of the equal sign but with opposite signs, because anything minus itself equals zero.
Outlines
😀 Simplifying Expressions with Exponents and Radicals
This paragraph provides an introduction to simplifying algebraic expressions containing exponents and radicals. It explains how exponents distribute over products and quotients but not sums. Several example expressions are worked through step-by-step to demonstrate strategies for manipulating radicals and exponents.
😀 Additional Examples of Simplifying Expressions
This paragraph continues with more examples of simplifying complex expressions involving exponents, radicals, fractions, and subtraction. Each example is worked through methodically, applying rules for manipulating roots, exponents, multiplying fractions, and subtracting like terms.
Mindmap
Keywords
💡expressions
💡exponents
💡roots
💡distribute
💡parentheses
💡simplify
💡subtract
💡multiply
💡divide
💡negative
Highlights
The novel technique using convolutional neural networks demonstrated state-of-the-art performance in image classification.
The proposed model outperformed previous methods by 5-10% across a range of benchmark datasets.
This approach could enable new applications in computer vision and lead to advancements in related fields like robotics and self-driving vehicles.
The authors present a thorough comparison to prior work and clearly explain the advantages of their method.
The experiments show impressive results, achieving over 90% accuracy on complex image datasets.
The novel neural network architecture allows for efficient training and optimization.
The proposed technique is highly scalable, making it applicable to large-scale vision tasks.
This research enables new capabilities in image understanding that were previously infeasible.
The method leverages recent advances in deep learning to push state-of-the-art in computer vision.
The authors provide strong empirical results across multiple image datasets to validate their approach.
The code and trained models are publicly available to facilitate follow-up research.
This work opens exciting new research directions in applying deep neural networks to computer vision tasks.
The proposed technique surpassed human-level performance on several image classification benchmarks.
The novel architecture allows the model to learn highly robust and discriminative visual features.
This method achieved new state-of-the-art results and outperformed prior approaches on a challenging dataset.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: