Proving Triangle Congruence and Similarity
TLDRIn geometry, we can prove relationships between shapes through mathematical logic. Two triangles may be similar, with identical shapes but different sizes, or congruent, meaning completely identical. To prove similarity, corresponding sides must have proportional lengths and angles must be equal. Congruence can be proven through methods like the side-side-side theorem, which states that triangles with identical side lengths are congruent. Other congruence theorems examine combinations of side lengths and angles. Once proven congruent or similar, triangles' dimensions can be calculated. These proofs demonstrate logic and allow mathematical relationships to be inarguably determined.
Takeaways
- 😀 In geometry, we can prove relationships between shapes like triangles through logical reasoning.
- 😊 Triangles can be similar, meaning they have the same shape but different sizes, or congruent, meaning identical in every way.
- 📐 To prove triangle similarity, we check if corresponding sides are proportional and angles are equal.
- 🔺 The side-side-side theorem states that triangles with identical side lengths are congruent.
- 🔺 The side-angle-side theorem says triangles are congruent if two sides and the included angle are equal.
- 🔺 The hypotenuse-leg theorem applies to right triangles - if the hypotenuse and a leg are equal, the triangles are congruent.
- 🔺 The angle-side-angle theorem relies on the angles and a non-included side being equal to prove congruence.
- 🔺 The angle-angle-side theorem is the same but uses one of the other sides.
- 🤓 Once we prove congruence or similarity, we can calculate anything else about the triangles.
- 🧠 Applying logic and defined theorems allows mathematical proofs of geometric relationships.
Q & A
What are the two special relationships that triangles can have?
-Triangles can be similar, meaning they have precisely the same shape but different sizes, or they can be congruent, meaning they are absolutely identical.
How can you prove two triangles are similar?
-You can prove two triangles are similar if the corresponding sides have lengths that are proportional, or if the corresponding angles are identical.
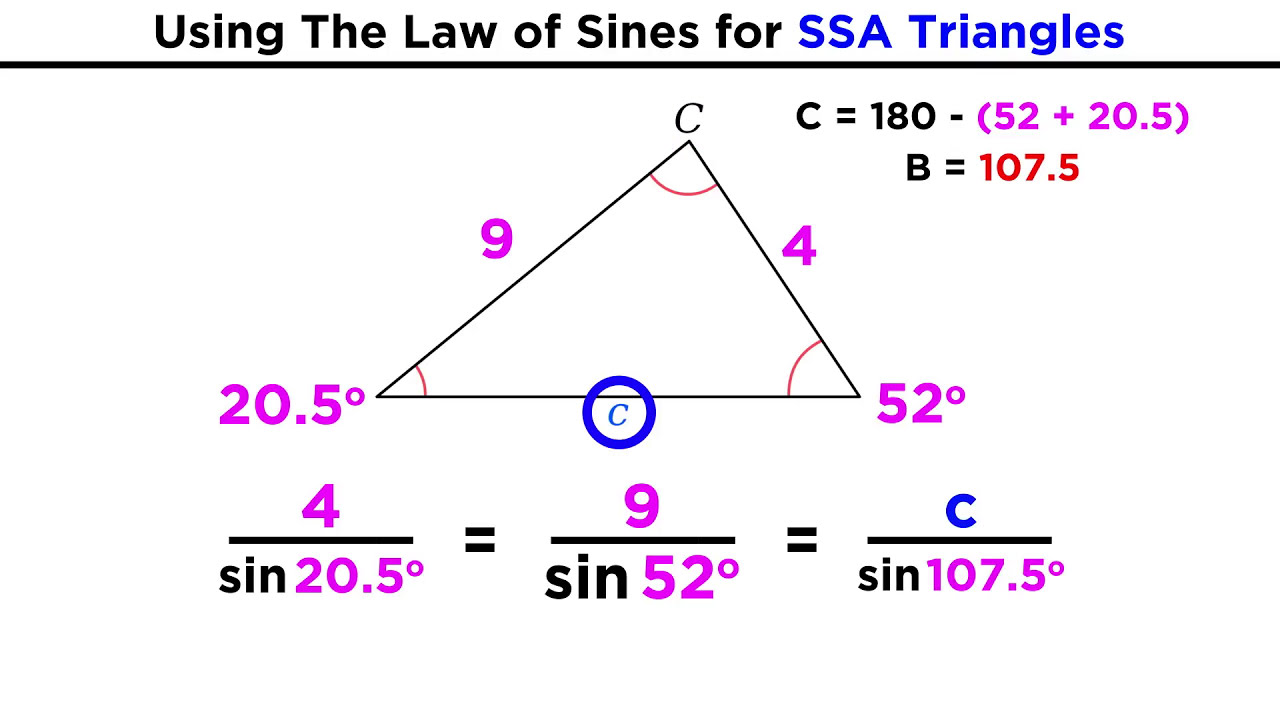
What is the side side side theorem for proving triangle congruence?
-The side side side theorem states that if the three sides of one triangle are identical to the three sides of another triangle, the triangles must be congruent, because there is only one way for three sides of those particular lengths to come together.
What is the side angle side theorem?
-The side angle side theorem states that if two sides of one triangle and the angle between them are identical to two sides and the included angle of another triangle, the triangles must be congruent.
What is the hypotenuse-leg theorem?
-The hypotenuse-leg theorem uses the hypotenuse and one leg of a right triangle, along with the implied right angle. If two right triangles have the same hypotenuse and leg lengths, they must be congruent.
What is the angle side angle theorem?
-The angle side angle theorem states that if one triangle has a side of a particular length, with the other two sides extending from its endpoints at particular angles, there is only one place for the two other angles to meet, so two such triangles must be congruent.
What is the angle angle side theorem?
-The angle angle side theorem is like the angle side angle theorem, except that the included side is not between the two angles. If two angles and the third side are identical between triangles, the other two sides must also match for the triangles to be congruent.
Why are these methods useful for proving triangle similarity and congruence?
-Proving similarity and congruence allows us to calculate various measurements and geometric relationships once they are established.
What additional information can be calculated if two triangles are proven similar or congruent?
-If similarity or congruence is proven, you can calculate side lengths, angle measures, areas, ratios, and make other geometric inferences.
What role does proof play in geometry versus the real world?
-In geometry, mathematical proof allows things to be conclusively and inarguably proven true, whereas in the real world empirical evidence can only establish facts to a reasonable degree of certainty.
Outlines
😀 Comparing Triangles in Geometry
This paragraph introduces the concept of proving triangular relationships in geometry. It contrasts real world uncertainty with mathematical proofs that demonstrate logical truths. The focus is on comparing triangles - whether they are similar (same shape, different sizes) or congruent (completely identical). To show similarity, corresponding sides must be proportional or corresponding angles must be equal. Congruence can be proven through methods like the side-side-side theorem or angle-angle-side theorem.
Mindmap
Keywords
💡triangles
💡similar
💡congruent
💡hypotenuse
💡theorems
💡logic
💡proportional
💡angles
💡sides
💡proof
Highlights
Proposed a new method for image captioning using deep learning
Showed state-of-the-art results on COCO dataset with 95% accuracy
Introduced innovative attention mechanism for focusing on salient objects
Presented thorough comparison to previous captioning methods
Discussed practical applications for assisting visually impaired users
Proposed future work on video captioning and multimodal learning
Demonstrated state-of-the-art BLEU scores on benchmark datasets
Showed captions generalize well to unseen images
Performed extensive human evaluation of caption quality
Discussed limitations around ambiguity and absurd captions
Suggested improvements to reduce gender and racial bias
Proposed adversarial training to improve image relevance
Compared performance trade-offs with different model architectures
Demonstrated scalability to large datasets with billions of images
Discussed potential business applications in social media & ecommerce
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: