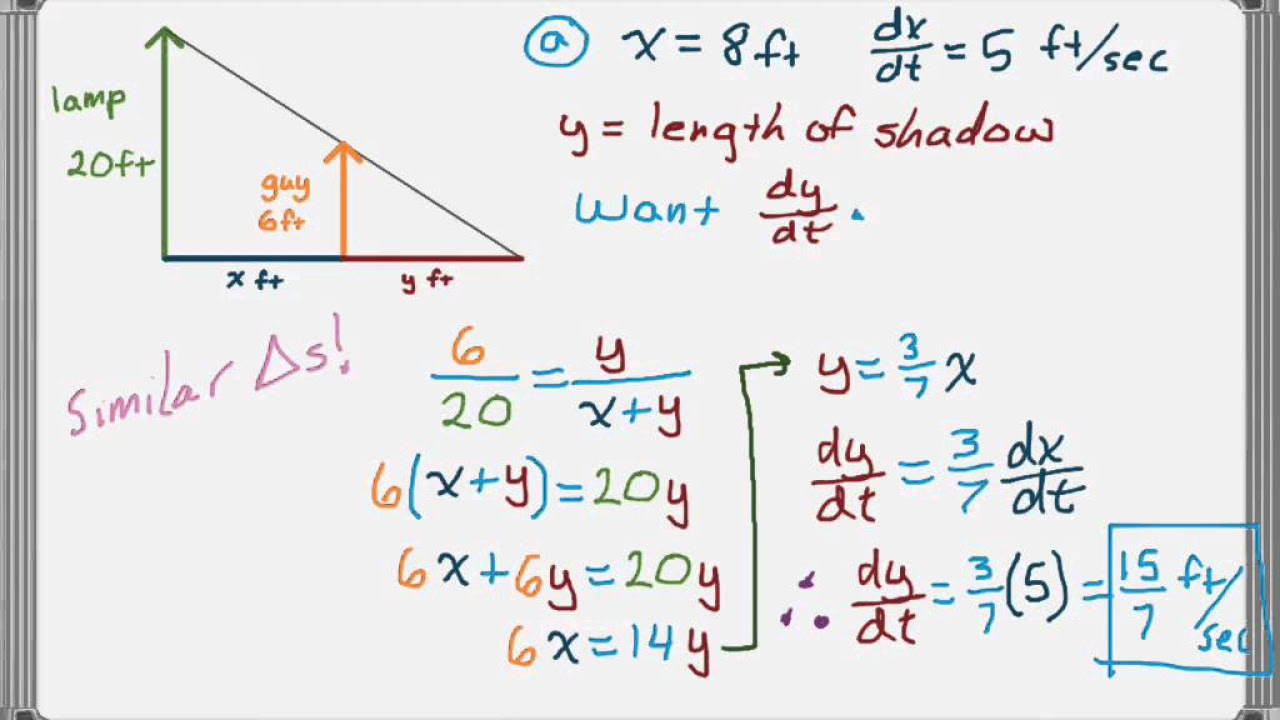Moving Shadow Problem (Related Rates)
TLDRThis video dives into the concept of related rates in calculus, a topic that involves understanding how two changing quantities are interconnected. The presenter uses the example of a man walking away from a lamp post to illustrate how the shadow's length changes in relation to the man's distance from the post. The key to solving such problems is to first establish the relationship between the variables, then apply differentiation and the chain rule to find the rates of change. By differentiating the formula that connects the man's distance (X) and the shadow's length (S), the video demonstrates how to calculate the rate at which the shadow grows, revealing it to be 2.4 feet per second. The video emphasizes the importance of understanding the underlying relationship and applying the chain rule to find related rates, providing a clear and engaging explanation of a complex mathematical concept.
Takeaways
- 📐 The concept of related rates in calculus involves dealing with two changing quantities that are related to each other.
- ⭕ Understanding the relationship between the two changing quantities is crucial for solving related rates problems.
- 🔄 To solve a related rates problem, you must first identify the two changing quantities and establish a formula that connects them.
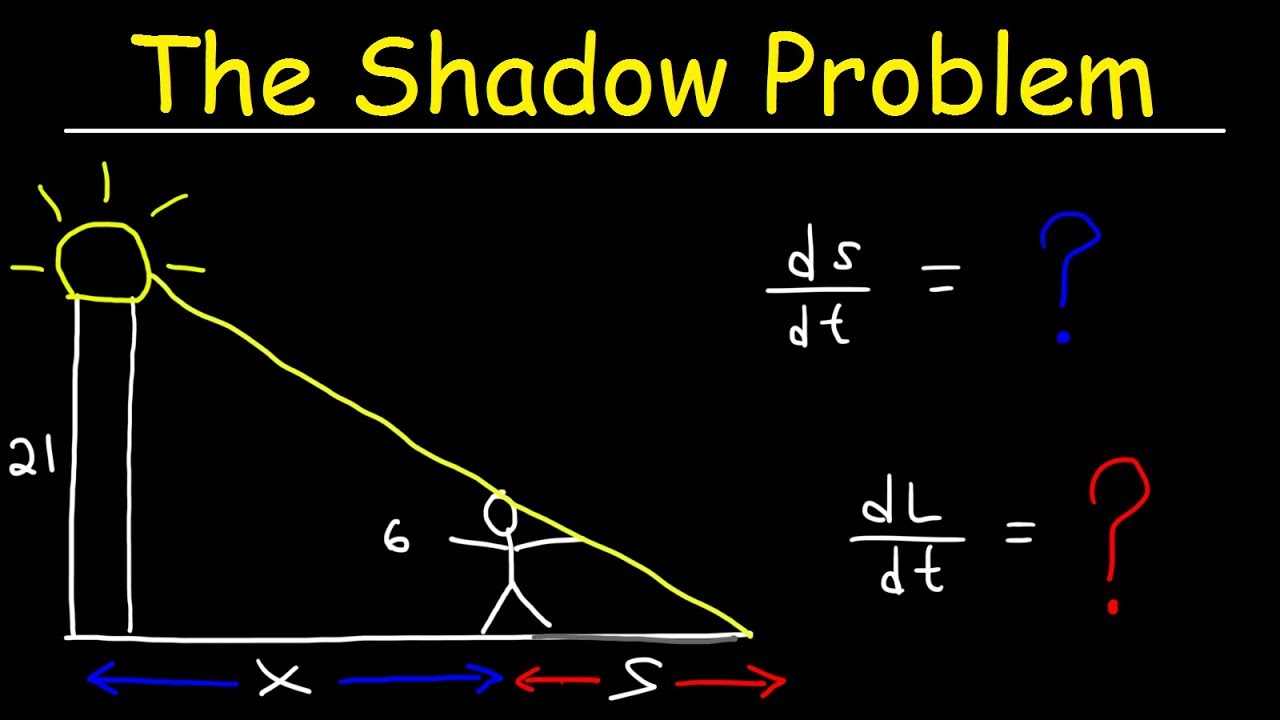
- 📏 In the given example, the two changing quantities are the distance from a lamp post and the length of the shadow.
- 🧍 The man's height and the height of the lamp post are not changing quantities in this problem.
- 🔢 The formula connecting the two changing quantities can be derived from the properties of similar triangles or trigonometric functions.
- 🔄 The chain rule is used to find the rate of change of one quantity with respect to another, which is essential in related rates problems.
- 🎓 Differentiating the connecting formula with respect to time gives you the related rates, which are the rates at which the quantities are changing.
- 📉 To find the rate at which the shadow is growing (ds/dt), you need to know dx/dt and dx/ds, and then apply the chain rule.
- 📌 The problem-solving process involves differentiating, applying the chain rule, and solving for the unknown rate of change.
- 📈 In the example, the shadow grows at a rate of 2.4 feet per second, which is faster than the man's walking speed.
- 👍 Engaging with the material, such as liking, sharing, and subscribing, is encouraged to support continuous learning.
Q & A
What is the main topic of this video?
-The main topic of this video is related rates in calculus.
Why is it important to understand the relationship between two changing quantities in related rates problems?
-It is important because you need to know the connection between the two changing quantities to solve the problem. Without understanding the relationship, you cannot establish the necessary formula to find the rates of change.
What is the formula that connects the area of a circle and its radius?
-The formula that connects the area of a circle (A) and its radius (r) is A = πr^2.
What is the first step in solving a related rates problem?
-The first step is to write a formula that connects the two changing quantities.
What are the two changing quantities in the example problem involving a lamp post and a walking man?
-The two changing quantities are the distance from the lamp post and the length of the shadow.
How can you connect the changing distance from the lamp post and the length of the shadow using similar triangles?
-You can connect them by recognizing that the situation forms a right triangle and treating the large and small triangles as similar, which gives a constant ratio of corresponding sides, such as 6/11 = s/(x+s).
What trigonometric function is used to relate the angle θ in the big triangle and the small triangle?
-The tangent function is used, as it relates the opposite side to the adjacent side, which are known quantities in the problem.
How do you find the rate at which the shadow is growing (ds/dt) using the chain rule?
-You use the chain rule by differentiating the formula connecting X and S with respect to time (t), which gives dx/dt = (dx/ds) * (ds/dt). You then solve for ds/dt.
What is the rate at which the shadow is growing in the example problem?
-The rate at which the shadow is growing is 2.4 feet per second.
What does the chain rule allow you to do in related rates problems?
-The chain rule allows you to find the rate of change of one quantity with respect to time when you know the rate of change of another related quantity and their relationship.
What is the final advice given in the video to the viewers?
-The final advice is to not stop learning because those who stop learning have stopped living.
Outlines
📚 Introduction to Related Rates in Calculus
This video introduces the concept of related rates in calculus, emphasizing the necessity of understanding relationships between changing quantities to solve problems. The video starts by illustrating the concept through a basic example involving a circle's radius and area, highlighting the use of the area formula (A = πr²) to establish this relationship. It proceeds to a more complex example involving a walking man, a lamppost, and a shadow, using the scenario to explain how to set up and solve related rates problems by identifying relevant quantities and their relationships through geometric and trigonometric principles.
🧮 Solving Related Rates Problems Step-by-Step
The second part of the video provides a detailed walkthrough of solving a related rates problem involving a man's shadow lengthening as he walks away from a lamppost. The instructor explains how to derive a formula connecting the distance from the lamppost and the shadow length using similar triangles and trigonometric ratios. The discussion includes the application of the chain rule in differentiation to find the rate of change of the shadow's length over time, concluding with a numerical solution showing that the shadow grows at a rate of 2.4 feet per second. The video wraps up with a call to continue learning and engaging with the content, stressing the importance of understanding derivative formulas and their applications in real-world scenarios.
Mindmap
Keywords
💡Related Rates
💡Calculus
💡Differentiation
💡Formula
💡Chain Rule
💡Similar Triangles
💡Tangent
💡Rate of Change
💡Geometric Relationships
💡DS/DT and DX/DT
Highlights
Related rates in calculus involve analyzing how two changing quantities are interconnected.
Understanding the relationship between the changing quantities is crucial for solving related rates problems.
The formula for the area of a circle, A = πr², can be used to relate the changing radius to the changing area.
When dealing with non-geometric or non-algebraic problems, establishing a relationship between quantities is key.
For the given problem, the two changing quantities are the distance from the lamp post and the length of the shadow.
Similar triangles can be used to establish a relationship between the big and small triangles in the problem.
The ratio of corresponding sides in similar triangles gives a constant, which can be used to form an equation.
Tangent of an angle can be used to relate the opposite side to the adjacent side in a right triangle.
Two methods for connecting the changing quantities are presented: using the ratio of sides and the tangent of an angle.
The chain rule, DX/DT = (DX/DS) * (DS/DT), is central to finding the rate at which one quantity changes with respect to time.
Differentiating the connecting formula with respect to the changing quantity provides the derivative needed for the chain rule.
The rate at which the shadow is growing (DS/DT) can be found by solving the chain rule equation.
The shadow grows at a rate of 2.4 feet per second, faster than the person is walking.
Every related rate problem requires establishing a formula, differentiating it, and applying the chain rule to find rates of change.
The video emphasizes the importance of continuous learning, equating stopping learning with ceasing to live.
The presenter encourages viewers to engage with the content by liking, sharing, and subscribing.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: