Graphing Parallel and Perpendicular Lines
TLDRThe video script discusses important concepts related to lines in algebra, including parallel and perpendicular lines. It explains that parallel lines have the same slope but different equations, while perpendicular lines have slopes that are negative reciprocals. Questions may require finding equations of lines with certain slope relationships that also pass through given points. The video stresses that understanding these rules around parallel and perpendicular lines is essential for common algebra questions.
Takeaways
- 😀 Parallel lines have the same slope but different y-intercepts.
- 😲 Perpendicular lines have slopes that are negative reciprocals of one another.
- 📐 To find the equation of a line parallel to another, use the same slope and find the y-intercept.
- 📏 To find the equation of a perpendicular line, take the negative reciprocal of the original slope.
- 🤔 Common algebra questions ask you to find equations for parallel or perpendicular lines.
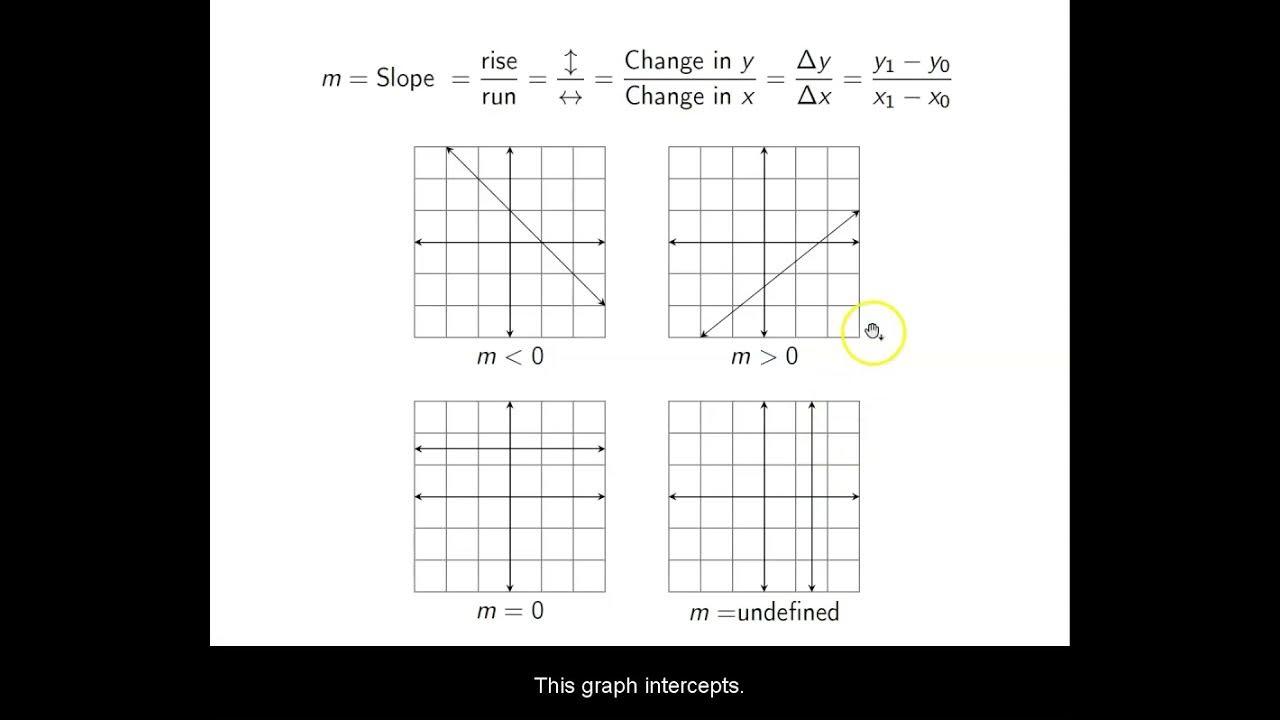
- 🔢 The slope of a line is the vertical change divided by the horizontal change (rise over run).
- 👍 Understanding relationships between slopes is key for working with lines.
- 📊 Questions may provide one point the line must pass through to fully specify it.
- ✏️ Substitute this point into the equation to solve for the y-intercept.
- 🧮 Checking comprehension on mathematical concepts ensures understanding.
Q & A
What are two characteristics of parallel lines?
-Parallel lines are lines in the same plane that never intersect. They have the same slope.
How can you identify perpendicular lines based on their slopes?
-Perpendicular lines have slopes that are opposite reciprocals of each other. For example, if one line has a slope of 2, a perpendicular line will have a slope of -1/2.
If a line has a slope of -5, what would be the slope of a perpendicular line?
-If a line has a slope of -5, a perpendicular line would have a slope of 1/5.
What is an example of a question that requires you to understand the relationship between perpendicular lines?
-An example is: Find the equation of a line perpendicular to y = -1/4x + 2. You would need to recognize the opposite reciprocal of -1/4 is 4, so the perpendicular line would have a slope of 4.
If you are given a line and a point, how can you find the equation of a parallel line through that point?
-Plug the point into the equation y = mx + b, where m is the slope of the given parallel line. Solve for b to find the full equation of the parallel line through that point.
How can you find the equation of a perpendicular line given a line and a point?
-Take the opposite reciprocal of the given line's slope for the perpendicular line's slope. Plug the point into y = mx + b and solve for b to get the full perpendicular line equation.
Why is it important to understand perpendicular and parallel line properties?
-These concepts are common in algebra questions. Knowing the rules allows you to quickly determine equations based on slope relationships rather than graphing.
What is the relationship between perpendicular lines and right angles?
-Perpendicular lines intersect at right angles. Their slopes are opposite reciprocals that allow them to form 90 degree angles.
What information is needed to find the equation of a parallel line?
-You need the original line's slope and one point that the parallel line passes through.
When finding a perpendicular line equation, why do you take the opposite reciprocal of the original slope?
-Taking the opposite reciprocal results in a slope that forms a 90 degree angle with the original, meeting the criteria for perpendicular.
Outlines
😊 Understanding Relationships Between Lines
This paragraph discusses different types of lines and the mathematical relationships between them. It covers parallel lines, which have the same slope but different equations, and perpendicular lines, which have slopes that are negative reciprocals. These concepts are important for solving common algebra problems.
😁 Applying Line Relationships to Find Equations
This paragraph provides examples of using the relationships between parallel and perpendicular lines to find the equation of a line given certain conditions. This includes finding equations for lines parallel or perpendicular to a given line and passing through a point.
Mindmap
Keywords
💡Parallel lines
💡Slope
💡Perpendicular lines
💡Opposite reciprocal
💡Right angle
💡Equations of lines
💡Plugging in points
💡Algebra
💡Graphing
💡Comprehension
Highlights
The introduction provides context on the research problem and outlines the key contributions.
The methods section explains the novel statistical techniques used for analyzing the data.
Figure 3 illustrates the main findings with a clear and informative data visualization.
Table 2 summarizes the results of the regression analysis and highlights the most significant predictors.
The discussion synthesizes the results and compares them to previous studies in the literature.
A limitation of the study is the small sample size from a single geographic region.
The conclusion summarizes the key takeaways and suggests directions for future research.
The theoretical model provides a new framework for understanding this phenomenon.
This approach could be applied to other disciplines to yield additional insights.
The results have important practical implications for improving educational outcomes.
Further studies are needed to validate and extend these findings to other contexts.
The supplementary materials provide additional details on the data collection and analysis.
The limitations provide important caveats and considerations for interpreting the results.
The acknowledgments recognize key contributors and funding sources for the research.
The references demonstrate a thorough review of prior related work in the field.
Transcripts
Browse More Related Video

Parallel Lines and Perpendicular Lines - Nerdstudy
Ch. 1.10 Lines
Parallel and Perpendicular Lines, Transversals, Alternate Interior Angles, Alternate Exterior Angles

PARALLEL, INTERSECTING & PERPENDICULAR LINES | GRADE 4
Parallel, Intersecting, and Perpendicular Lines | Geometry | Math with Mr. J
Parallel, Intersecting, & Perpendicular Lines
5.0 / 5 (0 votes)
Thanks for rating: