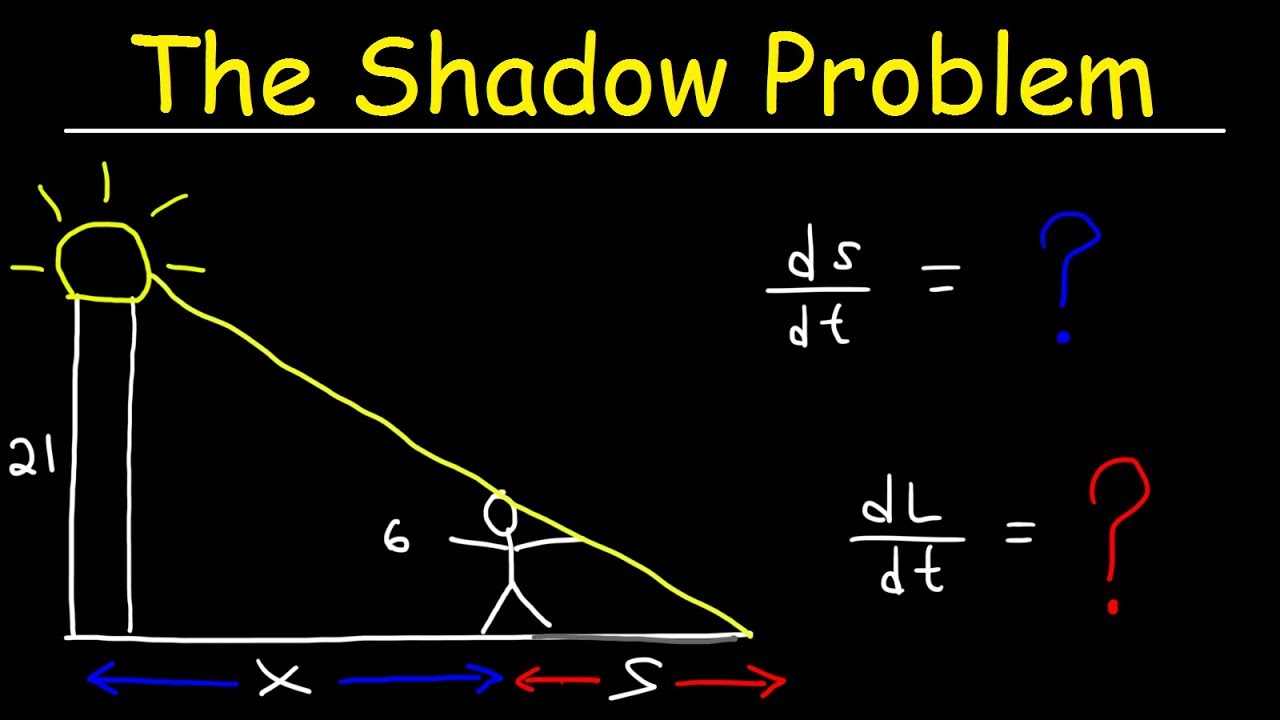
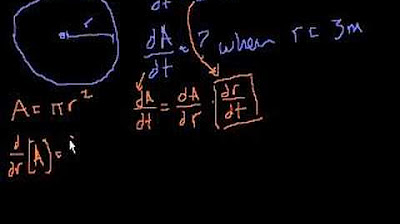How to solve a changing area of circle with related rates
TLDRThe video script discusses a mathematical problem involving a pebble dropped into a compound, creating ripples. The focus is on determining the rate of change of the disturbed water area as the ripples' radius increases at a rate of one foot per second. The radius is given as four feet, and the problem is solved by differentiating the area formula with respect to time, resulting in a rate of change of 8π square feet per second.
Takeaways
- 🔍 The problem involves a pebble dropped into a compound, creating ripples in the form of circles.
- 📐 The radius (r) of the ripples is increasing at a rate of one foot per second.
- 🎯 The initial radius (r) of the ripples is given as four feet.
- 🤔 The main question is to find the rate at which the total area of the disturbed water is changing.
- 👉 It's important to understand and restate the question to ensure solving the correct problem.
- 🧐 The rate of change of the radius (dr/dt) is known to be one foot per second.
- 📈 To find the change in area with respect to time, the area formula (A = πr²) must be differentiated with respect to time.
- 🌀 The derivative of the area (dA/dt) is expressed as 2πr * (dr/dt), combining constants for simplification.
- 📌 At the specific moment when the radius is four feet, the rate of change of the area is calculated.
- 🔢 The final expression for the rate of change of the area (dA/dt) is 8π feet per second squared or feet squared per second.
- 👨🏫 The script emphasizes the importance of verifying the solution against the question to ensure it answers the intended query.
Q & A
What is the main concept discussed in the video script?
-The main concept discussed in the video script is the rate of change of the total area of the disturbed water when a pebble is dropped into a compound causing ripples.
How are the ripples formed in the given scenario?
-The ripples are formed in the form of circles with the radius of the auto ripple increasing at a rate of one foot per second when a pebble is dropped into a compound.
What is the initial radius of the auto ripple mentioned in the script?
-The initial radius of the auto ripple mentioned in the script is four feet.
What is the rate of increase of the radius of the auto ripple?
-The radius of the auto ripple is increasing at a rate of one foot per second.
What is the formula used to calculate the area of the disturbed water?
-The formula used to calculate the area of the disturbed water is A = πr^2, where A is the area and r is the radius of the ripple.
How is the rate of change in the area with respect to time represented?
-The rate of change in the area with respect to time is represented by the derivative of the area formula with respect to time, which is dA/dt = 2πr * dr/dt.
What is the method used to find the rate of change of the total area of the disturbed water?
-The method used to find the rate of change of the total area of the disturbed water is differentiation, specifically with respect to time.
What is the significance of restating the question in solving word problems?
-Restating the question is significant in solving word problems as it ensures that the correct question is being addressed and the solution provided is relevant and accurate to the problem at hand.
What is the importance of verifying the solution against the question?
-Verifying the solution against the question is important to ensure that the work done leads to the correct answer and that the same problem, if asked in different ways, is not误解 解决.
What is the final calculated rate of change of the total area of the disturbed water when the radius is four feet?
-The final calculated rate of change of the total area of the disturbed water when the radius is four feet is 8π feet squared per second (8π ft^2/s).
How does the script emphasize the importance of understanding the problem?
-The script emphasizes the importance of understanding the problem by encouraging the restatement of the question and verifying the solution to ensure that the correct question is answered and the problem is solved accurately.
Outlines
🌊 Ripples in a Compound
This paragraph introduces a scenario where a pebble is dropped into a compound, creating ripples that form circles. The radius (r) of these ripples is increasing at a rate of one foot per second. The main focus is on understanding the rate at which the total area of the disturbed water (the area of the ripples) is changing when the radius is four feet. The speaker emphasizes the importance of restating the question to ensure that the correct answer is obtained, highlighting the need to differentiate the area formula with respect to time. The key information includes the rate of change of the radius (dr/dt) being one foot per second and the radius (r) being four feet at the time of interest. The mathematical expression derived to find the rate of change in area (dA/dt) is 2πr * dr/dt, which simplifies to 8π feet squared per second when the radius is four feet and the rate of increase is one foot per second.
Mindmap
Keywords
💡pebble
💡ripples
💡radius
💡area
💡rate of change
💡differentiate
💡pi (π)
💡circles
💡word problems
💡constants
💡 Feet per second
💡 Feet squared
Highlights
A pebble is dropped into a compound causing ripples to form in the shape of circles.
The radius of the ripples (r) is increasing at a rate of one foot per second.
When the radius is four feet, the problem focuses on determining the rate of change of the total disturbed water area.
The importance of restating the question to ensure the correct problem is being solved is emphasized.
The radius r of the auto ripple is increasing, which is a key piece of information for solving the problem.
The change in the radius (dr/dt) is given as one foot per second.
At the time of evaluation, the radius r is equal to four feet.
The goal is to find the rate of change of the area (da/dt) with respect to time.
The formula for the area of a circle (πr^2) needs to be differentiated with respect to time to find da/dt.
The differentiation of the area formula with respect to time results in 2πr(dr/dt).
When the radius increase rate is one foot per second and the radius is four feet, the calculation of da/dt is performed.
The final expression for the rate of change of the area is 8π feet per second squared or feet squared per second.
The problem-solving approach involves understanding the context, identifying variables and their rates, and applying calculus to determine the rate of change.
The process highlights the practical application of mathematical concepts such as rates of change and differentiation in real-world scenarios.
The transcript serves as an educational resource for teaching problem-solving techniques and mathematical concepts.
The problem and its solution demonstrate the importance of precision and accuracy in mathematical modeling and calculations.
The example problem provides a clear illustration of how to apply calculus to a physical situation involving growth rates and areas.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: