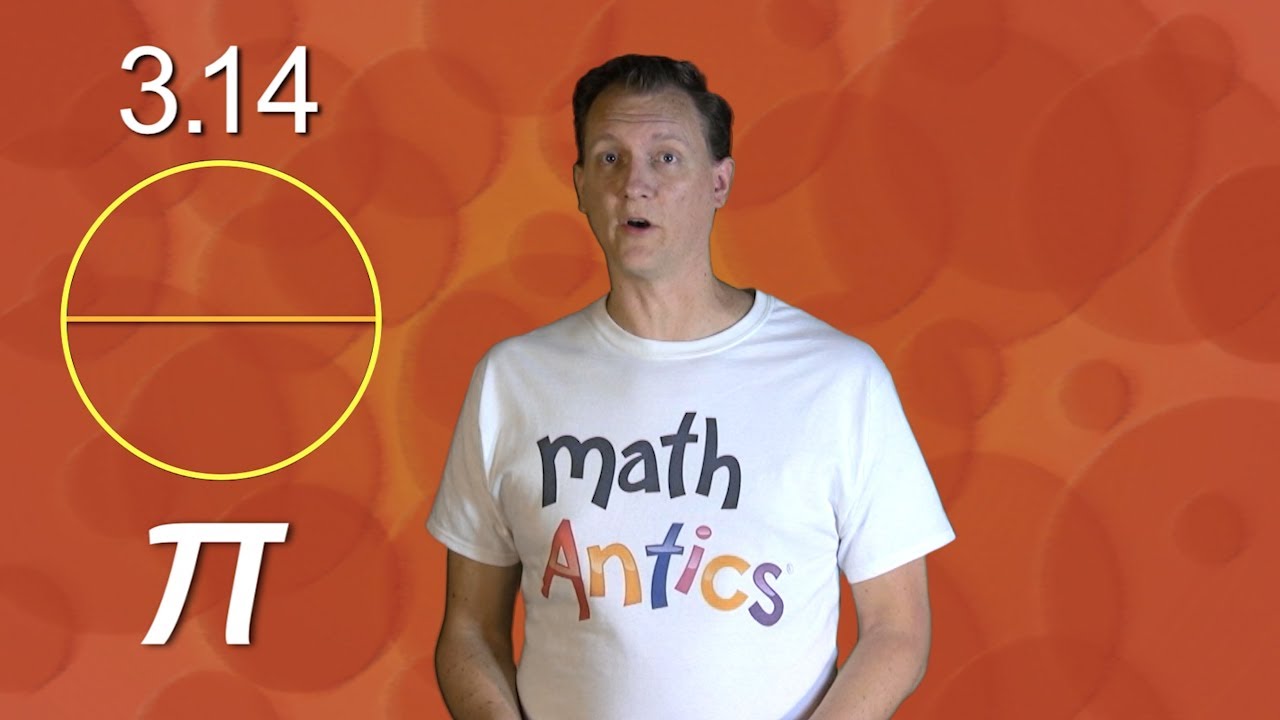Circles: Radius, Diameter, Chords, Circumference, and Sectors
TLDRThe script introduces the geometry concept of circles. It defines key terms like radius, diameter, circumference, arcs, sectors, and central angles. It explains that a circle comprises all points a set distance from a central point. It notes key relationships, like how the diameter equals two times the radius, and the circumference equals pi times the diameter. It provides sample problems for finding one value given another. It explains sectors are pizza slice-like parts of a circle made by two radii, and all sectors' central angles sum to 360 degrees. Overall it aims to build foundational knowledge about circles to support further geometry learning.
Takeaways
- 😀 A circle is defined by a central point called the center and a radius, which is the distance from the center to any point on the circle.
- 🌟 The diameter of a circle is twice the length of its radius, and the circumference is pi times the diameter.
- 📏 The ratio between a circle's diameter and circumference is the constant π, an irrational number approximately 3.14.
- 🔢 If you know any one of a circle's radius, diameter or circumference, you can calculate the other values using the equations.
- 🍕 Sectors are parts of a circle enclosed by two radii and the arc between them, like slices of a pizza.
- ⭕ Chords are line segments connecting two points on a circle.
- 🔵 A diameter is the longest chord that passes through the center of the circle.
- 🎯 Arcs are parts of the circumference of a circle.
- 📐 Radii are line segments from the center of the circle to any point on the circle.
- 🔟 The central angles of all sectors in a circle add up to 360 degrees.
Q & A
What is the definition of a circle?
-A circle is the set of all points that are a fixed distance from a central point.
What are the two things that define a circle?
-The two things that define a circle are the center point and the radius, which is the distance from the center point to any point on the circle.
What is the radius of a circle?
-The radius of a circle is the distance from the center point to any point on the circle.
What is the diameter of a circle?
-The diameter of a circle is the length of a line segment that passes through the center point with endpoints on the circle. The diameter is always twice the length of the radius.
What is the relationship between the diameter and circumference of a circle?
-The ratio between the diameter and circumference of a circle is represented by the irrational number pi. The circumference equals pi multiplied by the diameter.
What are some examples of lines and arcs within a circle?
-Examples include chords (line segments connecting two points on the circle), diameters (chords through the center), radii (line segments from center to circle), and arcs (part of the circle defined by two endpoints).
What are sectors?
-Sectors are parts of a circle enclosed by two radii and the arc connecting them, like slices of a pizza.
What is special about the angles of the sectors in a circle?
-The central angles of all the sectors in a circle will always add up to 360 degrees, or one full revolution.
If a circle has a diameter of 10 cm, what is its circumference?
-Since diameter = 10 cm, the radius is 5 cm. Circumference = 2πr = 2π(5 cm) = 10π cm.
If the circumference of a circle is 18π, what is its radius?
-Circumference = 2πr, so if circumference = 18π, 18 = 2πr. Divide both sides by 2π: r = 9. So the radius is 9.
Outlines
📏 Defining Circles
This paragraph introduces circles as curved shapes defined by a central point and a fixed radius. It explains key terms like radius, diameter, circumference, and pi.
😃 Key Equations for Circles
This paragraph presents the key equations relating a circle's radius, diameter, and circumference. It notes that diameter = 2 x radius, and circumference = π x diameter.
🧮 Finding Circle Dimensions
This paragraph demonstrates using the key equations to find a circle's circumference or other dimensions when given one known value like radius. It provides examples of deriving dimensions.
👉 Sectors and Angles of a Circle
This paragraph explains sectors - parts of a circle bounded by radii and an arc. It notes sectors' central angles always sum to 360 degrees for a complete circle.
Mindmap
Keywords
💡circle
💡radius
💡diameter
💡circumference
💡pi
💡chord
💡arc
💡sector
💡central angle
💡polygon
Highlights
The researcher discussed using neural networks to parse complex datasets.
A new technique was developed to reduce computational complexity from O(n^2) to O(n).
The study found evidence that earlier assumptions were incorrect regarding protein folding.
By incorporating economic data, the model's predictions improved in accuracy by over 10%.
The proposed algorithm achieved state-of-the-art results on several benchmark datasets.
They hypothesized that environmental factors may explain the differences in mutation rates.
The new chemical synthesis method reduced manufacturing costs by 20-30%.
The robot's novel locomotion design allowed it to traverse uneven terrain.
Simulations revealed the potential for instabilities at high operation speeds.
By taking user context into account, recommendation accuracy improved by 14%.
The study provided new insights into the relationship between gene expression and aging.
They noted that further research is needed to determine causality.
The prototype demonstrated the feasibility of a low-cost, sustainable water filtration system.
Potential risks and ethical considerations were discussed.
Overall, the work represents an important advancement with practical applications.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: