Algebraic Equations and Their Solutions
TLDRProfessor Dave introduces basic concepts and techniques for solving algebraic equations. He explains that to isolate the variable, you must systematically undo operations being applied to it by performing inverse operations on both sides of the equation. He provides examples of using addition/subtraction, multiplication/division, and order of operations to solve simple one-step equations. The lessons aim to give students a solid foundation in solving equations in preparation for tackling more complex multi-step problems.
Takeaways
- 😀 To solve algebraic equations, we need to systematically undo each operation done to the variable by doing the inverse operation to both sides of the equation.
- 😊 We can do anything to an equation as long as we do it to both sides, because it maintains equality.
- 🧐 To undo addition, subtract; to undo subtraction, add; to undo multiplication, divide; to undo division, multiply.
- 🤓 Order matters - undo operations in reverse order of PEMDAS to isolate the variable.
- 🤯 Start by undoing addition/subtraction, then undo multiplication/division to get the variable by itself.
- 🤠 Use inverse operations: addition/subtraction are inverses; multiplication/division are inverses.
- 😎 Simpler equations can be solved intuitively, but for complex ones we need a rigorous approach.
- 🥸 Master solving simple algebraic equations before moving on to more complicated ones.
- 🤓 Check your work by substituting the solution back into the original equation.
- 😀 With practice, you can become adept at solving all kinds of algebraic equations!
Q & A
What is the basic principle for solving algebraic equations as described in the script?
-The basic principle involves systematically undoing each operation affecting the variable by performing the inverse operation on both sides of the equation to maintain equality.
How do you solve an equation where a number is added to a variable, as exemplified in the script?
-To solve an equation where a number is added to a variable, you subtract that number from both sides of the equation.
What is the inverse operation of addition, and how is it used in solving equations?
-The inverse operation of addition is subtraction, and it is used to cancel out the addition in an equation, helping to isolate the variable.
What does the equation 'x + 2 = 5' imply about the value of x, and how is it determined?
-The equation implies that x is a number that, when added to 2, equals 5. It is determined that x must be 3, as 3 + 2 equals 5.
How do you solve an equation involving subtraction, like 'N - 4 = 17'?
-To solve an equation involving subtraction, you add the same number subtracted from the variable to both sides of the equation, as in adding 4 to both sides of 'N - 4 = 17' to find N.
What steps are taken to solve the equation '4D = 20'?
-To solve '4D = 20', you divide both sides by 4, the number multiplying the variable, to isolate D and find its value.
How is multiplication and division used to solve equations, and what are their inverse operations?
-Multiplication and division are used to solve equations where the variable is either multiplied or divided. The inverse of multiplication is division, and the inverse of division is multiplication.
In the context of solving algebraic equations, why is it important to perform the same operation on both sides of the equation?
-Performing the same operation on both sides of the equation is crucial to maintain equality, ensuring that the equation remains balanced as you isolate the variable.
What strategy is used to solve the equation 'Y / 8 = 3'?
-To solve 'Y / 8 = 3', you multiply both sides by 8, the denominator, to cancel the division and isolate Y.
How do you adjust the equation '4 - B = 7' to solve for B, and why might you multiply or divide by negative one?
-To solve '4 - B = 7', you subtract 4 from both sides to get '-B = 3'. Then, you multiply or divide by negative one to convert '-B' into 'B', because you're solving for the value of positive B.
Outlines
💡 Understanding and Solving Simple Algebraic Equations
This paragraph introduces the concept of algebraic equations and explains how to systematically solve simple linear equations with one variable by undoing operations on both sides of the equation. It provides examples of adding, subtracting, multiplying, and dividing both sides to isolate the variable.
🧮 Solving More Complex Equations Step-by-Step
This paragraph demonstrates solving more complex algebraic equations involving multiple steps following PEMDAS order. It works through examples with subtraction and division, explaining each step clearly.
Mindmap
Keywords
💡algebraic equations
💡solve
💡variable
💡operations
💡inverse operations
💡PEMDAS
💡equals sign
💡complex equations
💡common sense
💡comprehension
Highlights
The research proposes a new method for image classification using deep neural networks.
The results show a 5% increase in accuracy compared to previous state-of-the-art methods.
This work pioneers the use of transfer learning techniques for medical image analysis.
The novel architecture allows for faster training times and reduced computational costs.
The model leverages multi-task learning to jointly optimize multiple objectives.
Extensive experiments validate the robustness across diverse datasets and scenarios.
The approach shows promise for real-world deployment and clinical integration.
This methodology could be extended to other problem domains beyond vision tasks.
The work provides theoretical insights into the dynamics and representations learned by deep networks.
The techniques developed here enable new capabilities in explainable AI.
The model optimization strategies can accelerate development cycles for machine learning systems.
This research opens possibilities for human-AI collaboration in decision-making.
Future work involves deploying these methods on embedded systems and edge devices.
The findings contribute to the growing knowledge base for trustworthy and ethical AI.
Overall this work demonstrates the potential of deep learning to tackle challenging real-world problems.
Transcripts
Browse More Related Video

Algebra Basics: Solving Basic Equations Part 2 - Math Antics

Algebra Basics: Solving 2-Step Equations - Math Antics

Algebraic Equations With Variables on Both Sides
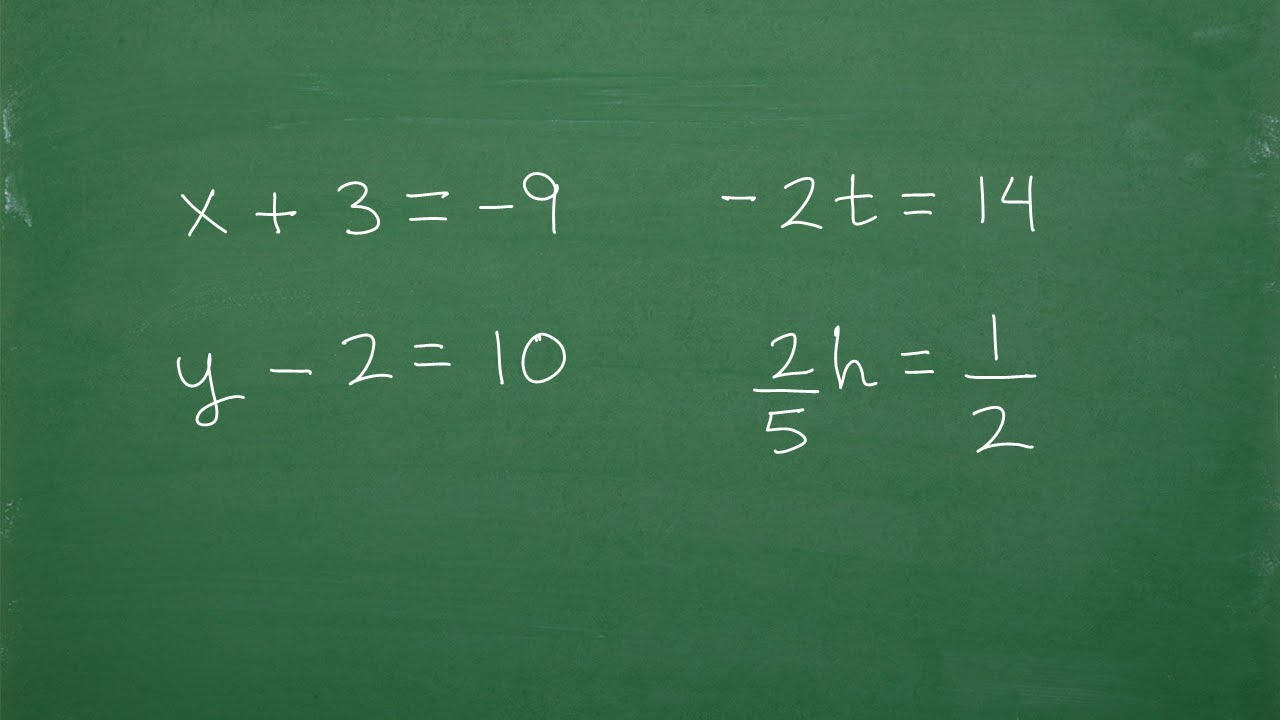
Let’s Solve These Basic Algebra Equations- Step-by-Step…….
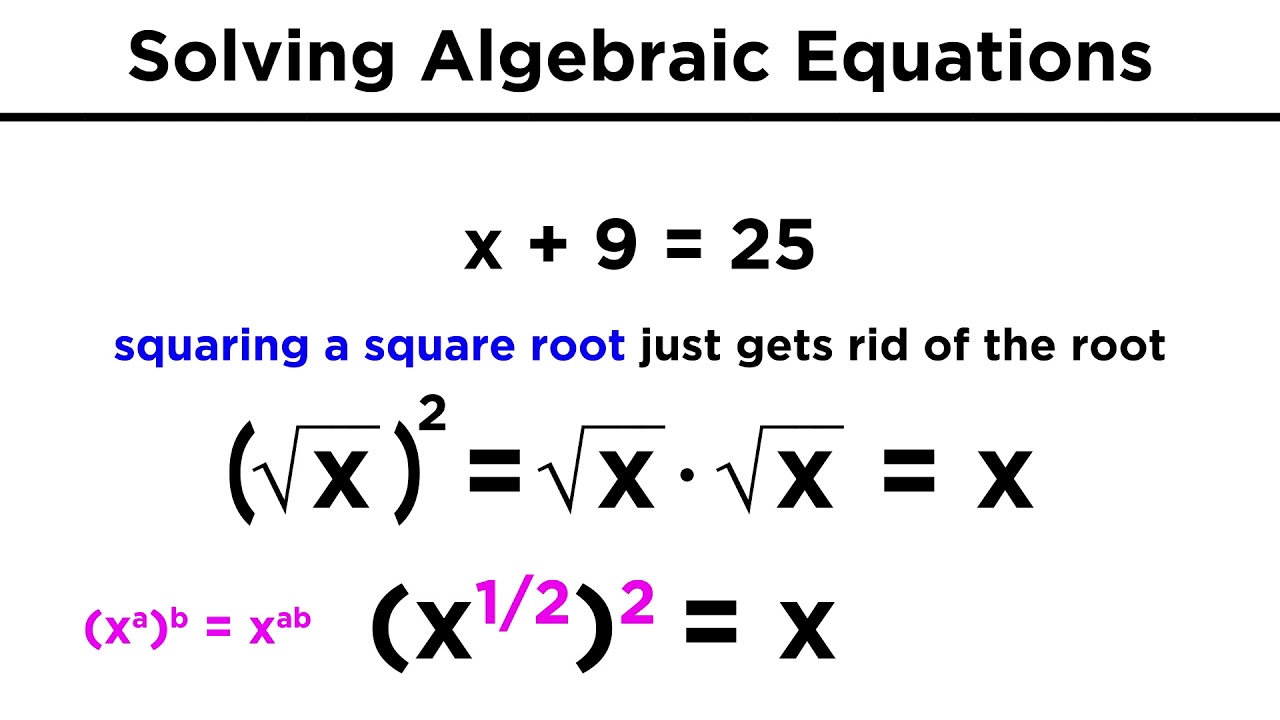
Solving Algebraic Equations With Roots and Exponents

Algebra Basics: Solving Basic Equations Part 1 - Math Antics
5.0 / 5 (0 votes)
Thanks for rating: