Calculus 1: Related Rates (Video #17) | Math with Professor V
TLDRThis video lecture on related rates explores how the rate of change of one quantity can be related to the rates of other interrelated quantities. The instructor uses examples such as a rectangle's changing dimensions, ships moving apart, and a filling trough to demonstrate how to set up and solve related rate problems. The key steps include understanding the given rates, setting up equations based on relationships between variables, differentiating with respect to time, and solving for the unknown rate. The lecture emphasizes the importance of units and the use of similar triangles in solving complex problems.
Takeaways
- 📚 The concept of related rates involves finding the rate of change of one quantity by relating it to other quantities whose rates of change are known or given.
- 🎯 When solving related rate problems, read the problem carefully, draw diagrams, introduce notation, and use derivatives to represent rates of change.
- 🔍 Identify the relationship between the variables involved by writing appropriate equations and then differentiating both sides with respect to time.
- 📈 For rectangles, the area (A) is related to the length (l) and width (w) by the equation A = l * w, and the rate of change of the area with respect to time is given by ∂A/∂t = l * ∂w/∂t + w * ∂l/∂t.
- 🏠 In the context of the ship problem, use the Pythagorean theorem to relate the changing distances (x, y, z) between two moving points and find the rate of change of the distance between them.
- 🛠️ When dealing with a trough or a container being filled, use the relationship between the volume (V) and the height (h) of the water to find the rate at which the water level is rising.
- 📐 For problems with similar triangles, use the properties of similar triangles to express one variable in terms of another, which simplifies the equation and allows for differentiation.
- 🔄 Always differentiate both sides of the equation with respect to time (t), using either implicit differentiation or the chain rule, as appropriate for the problem.
- 📌 Substitute the given values and rates of change into the differentiated equation to solve for the unknown rate.
- 🚀 Practice is essential for mastering related rate problems, which can become complex and exciting as more relationships and variables are introduced.
- 📋 Always ensure that units are consistent when performing calculations and interpreting rates of change.
Q & A
What is the main concept discussed in the video lecture?
-The main concept discussed in the video lecture is related rates, which involves finding the rate at which a quantity is changing by relating it to other quantities whose rates of change are more easily measured or given.
What is the strategy for solving related rate problems?
-The strategy for solving related rate problems includes reading the problem carefully, drawing a diagram when possible, introducing notation to represent rates of change using derivatives, expressing rates in terms of derivatives, writing an equation relating all the variables, and differentiating both sides of the equation with respect to time to solve for the unknown rate.
How does the rate of change have units, and why are they important?
-The rate of change has units because it involves a change over a period of time. The units are important as they help in interpreting the meaning of the rate of change and ensuring the correctness of the calculations. For example, if the rate is given in centimeters per second, it indicates a change in length with respect to time.
In the rectangle area increasing example, how is the area of the rectangle related to its length and width?
-In the rectangle area increasing example, the area of the rectangle is related to its length and width by the equation: Area (A) = Length (l) × Width (w). This relationship is used to find the rate of change of the area with respect to time.
What is the Pythagorean theorem used for in the ship distance changing example?
-In the ship distance changing example, the Pythagorean theorem is used to relate the horizontal and vertical distances traveled by the ships to the total distance between them. It states that in a right-angled triangle, the square of the length of the hypotenuse (the distance between the ships) is equal to the sum of the squares of the other two sides (the distances traveled east and north by the ships).
How is the volume of water in the trough related to the area of the triangular ends and the length of the trough?
-The volume of water in the trough is related to the area of the triangular ends and the length of the trough by the equation: Volume (V) = 1/2 × Base (b) × Height (h) × Length (l). The base and height change as the water level rises, and the length remains constant.
What is the significance of using similar triangles in solving related rate problems?
-Using similar triangles in solving related rate problems allows us to relate changing quantities that are proportional to each other. By establishing a relationship between the variables, we can eliminate variables that are not directly given, making it easier to solve for the unknown rate of change.
How is the rate of change of volume related to the rate of change of the water level height in the trough example?
-The rate of change of volume (dv/dt) is related to the rate of change of the water level height (dh/dt) by the equation: dv/dt = 30 × (dh/dt). This equation is derived from the volume formula V = 15h^2 and is used to find the rate at which the water level is rising when the water is six inches deep.
What is the final answer for the rate at which the water level is rising in the trough example?
-The final answer for the rate at which the water level is rising in the trough example is four-fifths of a foot per minute when the water is six inches deep.
How does the video lecture demonstrate the application of derivatives in real-world scenarios?
-The video lecture demonstrates the application of derivatives in real-world scenarios by showing how rates of change can be calculated for various situations, such as the increasing area of a rectangle, the changing distance between ships, and the rising water level in a trough. It uses the concept of related rates and the rules of differentiation to solve these problems.
What is the importance of implicit differentiation in related rate problems?
-Implicit differentiation is important in related rate problems because it allows us to differentiate both sides of an equation that relates variables without explicitly stating the derivative of each variable. This is particularly useful when solving for an unknown rate of change that is not directly given in the problem statement.
Outlines
📚 Introduction to Related Rates
This paragraph introduces the concept of related rates in calculus, focusing on how various quantities change over time. It uses the example of driving speed to illustrate the rate of change of distance with respect to time. The paragraph emphasizes the interrelation of rates of change and outlines the strategy for solving related rate problems, which includes reading the problem carefully, drawing diagrams, introducing notation for rates of change, expressing rates in terms of derivatives, and differentiating with respect to time to solve for the unknown rate. The paragraph sets the stage for the examples that follow, highlighting the importance of understanding how different quantities are interconnected and how their rates of change can be used to solve problems.
📈 Calculating the Rate of Change for a Rectangle's Area
This paragraph delves into a specific example of related rates, where a rectangle's length and width are increasing at different rates. The task is to find out how fast the area of the rectangle is increasing when the length is 20 centimeters and the width is 10 centimeters. The paragraph explains the process of differentiating the equation that relates the area of a rectangle to its length and width with respect to time. It demonstrates how to use the given rates of change (dl/dt and dw/dt) and the specific dimensions at a certain time to calculate the rate of change of the area (da/dt). The explanation includes the use of units to ensure the correctness of the calculation and sets up the foundation for understanding related rate problems involving geometric shapes.
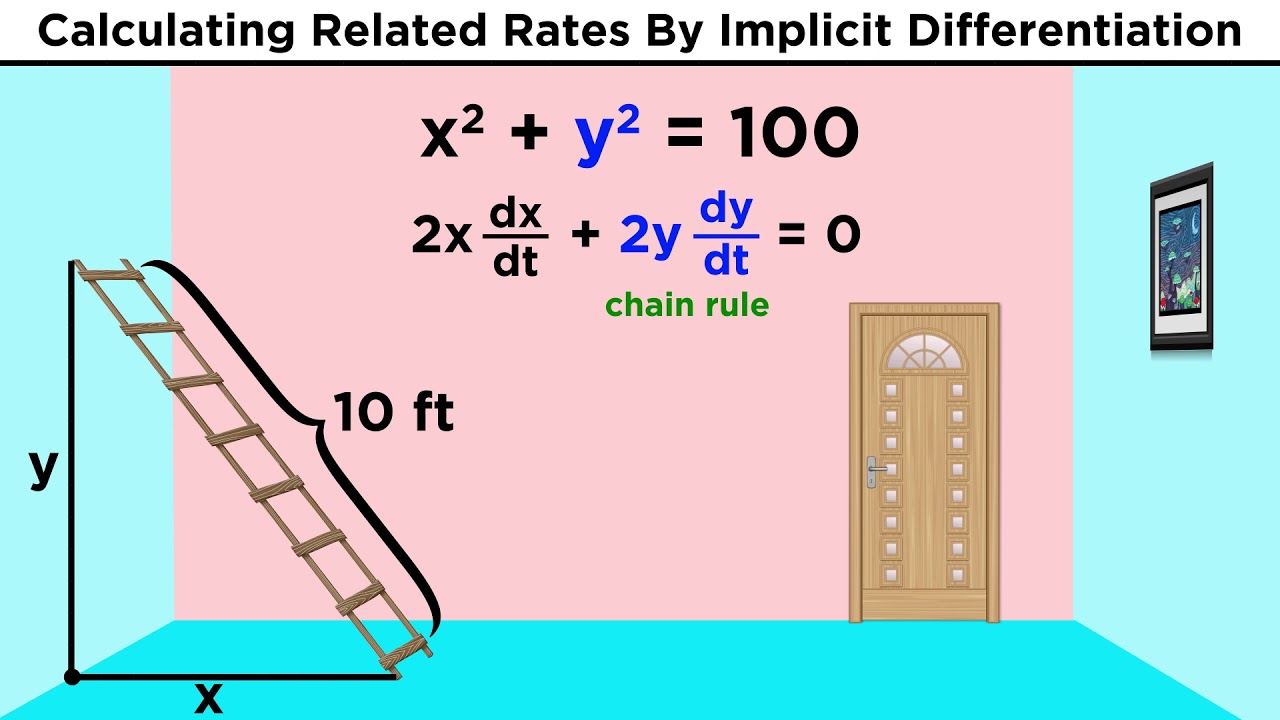
🔢 Solving for a Changing Coordinate Given a Rate of Change
This paragraph presents a mathematical problem involving the rates of change of x and y coordinates, given that x^2 + y^2 = 25 and dy/dt is known. The goal is to find dx/dt when y equals four. The paragraph explains the process of differentiating both sides of the given equation with respect to time and using the chain rule to account for the changing variables. It demonstrates how to solve for dx/dt by rearranging the differentiated equation and substituting the given values. The example also highlights the importance of considering the units in the problem and how they can help in interpreting the rate of change correctly.
🚢 Distance Change Between Two Ships
This paragraph tackles a more complex related rates problem involving two ships moving in different directions and the changing distance between them. The paragraph explains how to visualize the situation, set up the right triangle formed by the ships' positions and their relative motion, and apply the Pythagorean theorem. It details the process of differentiating the equation with respect to time to find the rate of change of the distance between the ships. The example illustrates how to use the given rates of change (dx/dt and dy/dt) and the specific positions of the ships at a certain time to calculate the rate of change of the distance (dz/dt). The explanation emphasizes the importance of units and precision in solving related rates problems.
💧 Rising Water Level in a Trough
This paragraph discusses a related rates problem involving a trough being filled with water and the rising water level. The paragraph describes the geometry of the trough, with isosceles triangular ends and a rectangular base. It explains the process of setting up an equation for the volume of water in the trough as a function of the water level height. The challenge is to find the rate at which the water level is rising when the water is six inches deep. The paragraph illustrates how to use similar triangles to eliminate the variable changing with time (the base of the triangular end) and how to differentiate the volume equation with respect to time to solve for the rate of change of the water level height (dh/dt). The example demonstrates the application of related rates in real-world scenarios and the importance of understanding geometric relationships.
🎓 Conclusion and Encouragement for Related Rates
The final paragraph wraps up the discussion on related rates by encouraging practice and highlighting the usefulness of similar triangles in solving such problems. It mentions a classic related rates problem involving a cone and provides a sneak preview of upcoming content on hyperbolic functions. The paragraph reinforces the importance of understanding the interconnectedness of quantities and their rates of change, and it invites the audience to engage with the content by liking the video and subscribing to the channel for more educational content.
Mindmap
Keywords
💡Related Rates
💡Derivatives
💡Rate of Change
💡Rectangle
💡Area
💡Differentiation
💡Strategy
💡Implicit Differentiation
💡Chain Rule
💡Pythagorean Theorem
💡Similar Triangles
Highlights
The lecture introduces the concept of related rates, which involve finding the rate of change of one quantity by relating it to other quantities whose rates of change are known or given.
A strategy for solving related rate problems is outlined, emphasizing the importance of reading the problem carefully, drawing diagrams, introducing notation, and expressing rates in terms of derivatives.
An example is provided where the length and width of a rectangle are increasing at different rates, and the goal is to find how fast the area is increasing.
The concept of using derivatives to relate variables in a problem is demonstrated, such as using the formula for the area of a rectangle (length times width) and differentiating both sides with respect to time.
A second example involves a system of two ships, where the rate of change of the distance between them is to be found using the given rates of the ships' movements and the Pythagorean theorem.
The use of the chain rule and implicit differentiation in related rate problems is discussed, as well as the importance of units in ensuring the correctness of the solution.
A third example deals with a trough being filled with water, where the rate of water level rise is to be determined based on the given volume filling rate and the geometry of the trough.
The concept of similar triangles is introduced as a method to handle problems with multiple changing variables, as illustrated by the varying base and height of the water level in the trough.
The lecture emphasizes the importance of units in calculations, as they help interpret the meaning of rates of change and ensure the accuracy of the results.
The process of differentiating both sides of an equation with respect to time is demonstrated, showing how to apply the product rule and other differentiation techniques in related rate problems.
The lecture provides a step-by-step approach to solving related rate problems, starting with simpler scenarios and gradually building up to more complex examples.
A practical application of related rates is shown through the example of the ships, where the rate of change of distance is relevant for navigation and collision avoidance.
The use of the Pythagorean theorem in solving related rate problems involving right triangles is highlighted, as seen in the example of the ships' distance.
The lecture concludes with a preview of upcoming topics, such as hyperbolic functions, indicating the continuity and progression of the calculus material being covered.
The importance of practice in mastering related rates problems is emphasized, encouraging students to apply the concepts and methods learned in the lecture to various scenarios.
The lecture demonstrates the integration of geometric principles, such as the Pythagorean theorem and concepts of similarity, with calculus techniques to solve real-world problems.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: