Related Rates

Stacy Colaiacovo

3 Jul 202335:34

EducationalLearning

32 Likes 10 Comments

TLDRThe video script presents a comprehensive lesson on related rates, a concept in calculus that involves differentiating equations with respect to time to find the rate of change of related variables. The instructor begins with an overview of the concept, emphasizing that related rates problems involve equations relating multiple variables that change over time. The lesson progresses by introducing the process of implicit differentiation with respect to time, which allows students to find new equations that relate the rates at which these variables change. The instructor then illustrates the concept with examples, such as calculating the rate at which the area of an oil spill is increasing given the rate of change of the radius. The script continues with detailed steps for solving related rates problems, including identifying variables, differentiating the given equation, and solving for the unknown rate of change. The lesson concludes with applications of related rates to real-world scenarios, such as calculating the rate of change of a sphere's volume, the rate at which water is draining from a tank, and the rate of change of revenue for a company producing peanuts. The instructor emphasizes the importance of careful reading and understanding of the problem, as well as the application of the chain rule during differentiation.

Takeaways

📚 **Related Rates Overview**: The concept of related rates involves multiple variables that are related by an equation and change over time.
⚙️ **Equation Differentiation**: Implicit differentiation with respect to time is used to find the relationship between the rates at which variables change.
🔄 **Chain Rule Application**: The chain rule is applied when differentiating equations with respect to time, especially when dealing with variables not explicitly in terms of time.
🌐 **Real-world Application**: Related rates are used to solve real-world problems, such as calculating the rate of change of an oil spill's area given the rate of change of its radius.
📉 **Derivative Significance**: Rates of change are essentially derivatives; when given a rate of change, it corresponds to the derivative of a variable with respect to time.
🔢 **Contextual Problem Solving**: In word problems, it's crucial to identify variables, list given information, and differentiate the given equation to find the unknown rate of change.
🏗️ **Volume and Rate of Change**: For a sphere's volume increasing at a certain rate, the rate of change of the radius can be found using the volume formula and its derivative with respect to time.
💧 **Draining Tanks**: The rate at which water drains from a cylindrical tank can be determined by differentiating the volume of the tank with respect to time and using the given rate of the water level drop.
📈 **Business Application**: In business, related rates can be used to find the rate of change of revenue given the rate of change of production, using the demand function and revenue formula.
🤝 **Unit Consistency**: It's important to maintain unit consistency throughout the problem-solving process to ensure the result's validity.
📝 **Detailed Calculation**: Careful calculation, including fraction management and potentially using a calculator or software like Desmos, is essential for accurate results.

Q & A

What is the main concept of related rates problems?
-The main concept of related rates problems involves two or more variables that are related by some known equation and are changing over time. The goal is to find an unknown rate by differentiating the given equation with respect to time, which introduces a new equation that relates the rates at which these variables are changing.
Why do we implicitly differentiate with respect to time in related rates problems?
-We implicitly differentiate with respect to time to introduce rates of change for each of the variables, which allows us to relate the rates at which each of the variables changes. This is essential for solving for an unknown rate when given certain values and rates in a problem.
What is the formula for the area of a circular patch in terms of its radius?
-The formula for the area of a circular patch in terms of its radius is Area = π * (radius)^2.
How do you find the rate at which the area of a circular patch is changing, given the rate at which its radius is changing?
-You would differentiate the area formula with respect to time to relate the rate of change of the radius to the rate of change of the area. Then, you would plug in the known rate of the radius and solve for the rate of change of the area.
What is the chain rule in the context of differentiation with respect to time?
-The chain rule in the context of differentiation with respect to time states that when differentiating a function of a variable that itself is a function of time, you multiply the derivative of the inner function (with respect to the variable) by the derivative of the variable with respect to time.
What is the process for solving related rates problems?
-The process involves: (1) Assigning variables to the unknowns in the problem, (2) Writing an equation that relates all the variables, (3) Implicitly differentiating this equation with respect to time, (4) Substituting known values into the differentiated equation, and (5) Solving for the unknown rate.
How do you ensure that your answer to a related rates problem is reasonable?
-You ensure your answer is reasonable by verifying the units of the answer make sense in the context of the problem and by checking that the magnitude of the answer is plausible given the known rates and values.
What is the formula for the volume of a sphere in terms of its radius?
-The formula for the volume of a sphere in terms of its radius is Volume = (4/3) * π * (radius)^3.
In the context of a cylindrical water tank being drained, what is the relationship between the rate at which the water level drops and the rate at which the volume of water decreases?
-The rate at which the water level drops (dh/dt) is directly related to the rate at which the volume of water decreases (dV/dt) through the formula for the volume of a cylinder, V = π * r^2 * h. As the height (h) decreases, the volume (V) also decreases, assuming the radius (r) remains constant.
How is revenue calculated in the context of a business problem?
-Revenue is calculated as the product of the number of units sold (X) and the price per unit (P). If the price is given as a function of the number of units, such as P = 50 - X/200, then revenue (R) is given by R = X * P.
What is the significance of finding the rate of change of revenue with respect to time in a business context?
-Finding the rate of change of revenue with respect to time allows a company to understand how quickly its income is increasing or decreasing per unit of time. This is crucial for making decisions about production rates, pricing strategies, and forecasting future earnings.

Outlines

00:00

📘 Introduction to Related Rates

This paragraph introduces the concept of related rates, explaining that it involves multiple variables changing over time and related by an equation. The focus is on understanding how these variables are interconnected and how their rates of change can be found by differentiating the given equation with respect to time.

05:01

🔗 Implicit Differentiation with Respect to Time

The paragraph explains the process of implicit differentiation with respect to time, which is essential for related rates problems. It covers the application of the chain rule when differentiating variables that are not explicitly a function of time, and how to introduce rates of change into the equation.

10:03

🌐 Applying Related Rates to Real-World Problems

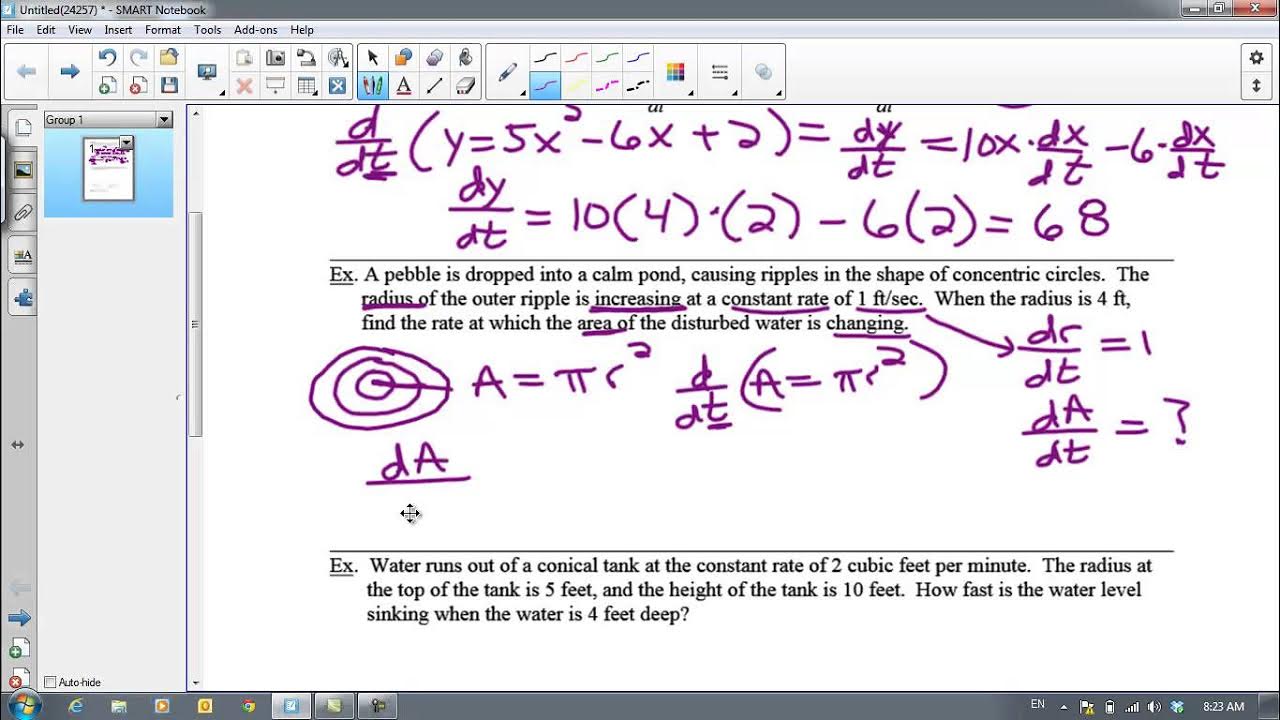
The speaker illustrates the application of related rates by discussing a real-world scenario involving an oil rig leak. The problem involves finding the rate of change of the oil patch's area given the rate of change of the radius. It demonstrates how to use the known relationship between the area and radius of a circle to solve for the unknown rate.

15:06

🧮 Solving Related Rates Problems Step by Step

This paragraph outlines the step-by-step process for solving related rates problems. It emphasizes the importance of assigning variables, listing given information, differentiating the equation relating the variables with respect to time, and then substituting known values to solve for the unknown rate of change.

20:06

📊 Volume and Radius Rates in a Sphere

The paragraph focuses on a problem where the volume of a sphere is increasing at a certain rate, and the task is to find the rate of change of the radius. It provides a detailed example of how to differentiate the volume formula of a sphere with respect to time and solve for the rate of change of the radius when given the rate of change of the volume.

25:09

🚰 Draining a Water Heater Tank

This section discusses a problem involving a water heater in the shape of a cylindrical tank. It explains how to find the rate at which water is draining from the tank by differentiating the volume formula of a cylinder with respect to time and solving for the rate of change of the water level given the rate at which the water level is dropping.

30:11

📈 Business Application: Peanut Production and Revenue

The final paragraph relates the concept of related rates to a business scenario where a company is increasing its production of peanuts. It presents a demand function and asks for the rate of change of revenue with respect to time when the daily production is at a certain level. The paragraph demonstrates how to use the given production rate, the demand function, and the revenue formula to find the desired rate of change.

35:11

📝 Summary of the Related Rates Process

The speaker summarizes the process for tackling related rates problems, emphasizing the need for careful reading and understanding of the problem statement. The paragraph concludes with an offer of help for those who need additional assistance, encouraging students to reach out if they encounter difficulties.

Mindmap

Keywords

💡Related Rates

Related rates are a fundamental concept in calculus where two or more variables are related through an equation, and these variables change over time. In the context of the video, related rates are used to solve real-world problems by differentiating the known equation with respect to time, which provides a new equation that relates the rates at which the variables change. An example from the script involves an oil rig leak, where the radius of the oil patch is increasing, and we want to find out how fast the area is changing.

💡Implicit Differentiation

Implicit differentiation is a technique used in calculus to find the derivative of an equation that does not explicitly contain the variable we are differentiating with respect to. In the video, it is used to differentiate the equation relating variables with respect to time. The process involves applying the chain rule and is crucial for finding the rates at which the variables are changing, as shown when differentiating the area of a circle in relation to its radius.

💡Chain Rule

The chain rule is a fundamental principle in calculus for differentiating composite functions. It states that the derivative of a function composed of two functions is the product of the derivative of the outer function and the derivative of the inner function. In the video, the chain rule is applied when differentiating equations with respect to time to find the rates of change of variables. An example is given when differentiating x^2 with respect to time, where x is a function of time.

💡Derivative

In calculus, a derivative represents the rate at which a function is changing at a certain point. It is a measure of sensitivity to change. In the context of the video, derivatives are used to find the rate of change of variables over time, which is essential for solving related rates problems. For instance, the derivative of the volume of a sphere with respect to time is used to find how fast the radius is changing when the volume is increasing at a given rate.

💡Equation of a Circle

The equation of a circle in the context of the video is A = πr^2, where A represents the area and r represents the radius of the circle. This equation is used to relate the area and radius of a circular oil patch spreading from an oil rig leak. By differentiating this equation with respect to time, one can find the rate at which the area of the oil patch is changing as the radius changes.

💡Volume of a Sphere

The volume of a sphere is given by the formula V = (4/3)πr^3, where r is the radius of the sphere. In the video, this formula is used to relate the volume and radius of a sphere whose volume is increasing at a certain rate. By differentiating this formula with respect to time, one can determine the rate at which the radius of the sphere is changing.

💡Rate of Change

The rate of change, often denoted as dy/dt or dx/dt, represents how quickly a variable is changing with respect to another variable, typically time. In the video, rates of change are used to solve for unknown rates in various scenarios, such as the rate at which the area of an oil patch is increasing or the rate at which the water level in a tank is dropping.

💡Product Rule

The product rule is a method used in calculus to differentiate the product of two functions. It states that the derivative of the product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the video, the product rule is applied when differentiating the volume of a cylinder with respect to time to find the rate at which water is draining from the tank.

💡Demand Function

A demand function, represented as P = 50 - X/200 in the video, is a mathematical relationship that shows how the price of a product (P) is influenced by the quantity produced or sold (X). The video uses this function to find the rate of change of revenue with respect to time when the production rate and price function are known.

💡Revenue Function

Revenue is the total income that a company receives from selling its products. In the video, the revenue function is R = 50X - X^2/200, which is derived from the demand function. This function is used to calculate the rate of change of revenue with respect to time, given the rate at which the company is increasing its production.

💡Units of Measurement

Units of measurement are used to express the magnitude of a physical quantity. In the context of the video, units are essential for ensuring that the rates of change and the solutions to the related rates problems are physically meaningful and consistent. For example, when calculating the rate of change of the radius of a sphere, the units are given as inches per second, indicating the change in radius with respect to time.

Highlights

The lesson provides an overview of related rates, a concept in calculus where two or more variables are related by an equation and change over time.

The process involves differentiating a known equation relating variables with respect to time to find rates of change.

An example of a real-life application is calculating how fast the area of an oil patch is changing given the rate of change of its radius.

The formula for the area of a circle (pi * radius squared) is used to relate the variables in the oil patch example.

Differentiating with respect to time requires the use of the chain rule, treating any variable not equal to time (t) as an inner function.

The lesson demonstrates how to implicitly differentiate an equation relating x and y, and then solve for an unknown rate of change.

The importance of understanding the context and identifying variables is emphasized for solving word problems.

An example of a business-related problem involves a company increasing its production of peanuts and the relation between price, demand, and revenue.

Revenue is calculated as the product of the number of units sold and the price per unit, leading to an equation that can be differentiated to find rates of change.

The lesson shows how to differentiate the revenue function with respect to time to find the rate of change of revenue.

Units of measurement are crucial for verifying that the answer to a related rates problem is reasonable.

A water heater problem is used to illustrate the concept of differentiating the volume of a cylinder with respect to time.

The rate of change of the radius is found for a sphere with a given rate of change of its volume, using the sphere's volume formula.

The process of implicit differentiation and the chain rule are applied to a variety of word problems to find unknown rates of change.

The importance of keeping consistent units throughout the problem-solving process is emphasized for accuracy.

A step-by-step approach is outlined for solving related rates problems, from identifying variables to differentiating and solving for the unknown rate.

The lesson concludes with a reminder to be careful with wording and units when approaching related rates problems.

Transcripts

Browse More Related Video

Math1325 Lecture 11-4 - Related Rates

Calculus AB Lesson 4.2: Related Rates

Related Rates Day 1

3.8/3.9 - Implicit Differentiation and Related Rates

Business Calculus - Math 1329 - Section 2.6 - Implicit Differentiation and Related Rates

BusCalc 12.5 Related Rates

Related Tags

Related Rates Calculus Lessons Implicit Differentiation Real-life Applications Mathematical Concepts Educational Content Chain Rule Derivatives Volume Analysis Business Math Oil Rigs Water Heaters Production Rates Revenue Functions