BusCalc 12.5 Related Rates
TLDRThe video script is an educational walkthrough of solving calculus problems involving implicit differentiation and related rates. The instructor begins by explaining how to find the derivative of an equation with respect to x when y is given implicitly. Using the product rule, they derive an expression for dy/dx. The second part of the script tackles an application problem involving the cost of printing business cards, where the relationship between cost and the number of cards is mathematically represented, and the rate of change is calculated using derivatives. The instructor emphasizes the importance of understanding the relationship between variables, applying implicit differentiation, and solving for the desired rate of change. They also discuss how to approach related rates problems by setting up an equation based on geometric or logical relationships, differentiating with respect to time, and solving for the rate of change. The script provides detailed steps and examples, including a ladder leaning against a wall and a scenario with a tanker and a barge moving in different directions. The final examples involve a spherical balloon inflating and a company adjusting its subscription price, demonstrating how to apply these calculus concepts to real-world problems.
Takeaways
- 📚 Implicit differentiation is used to find the derivative of an equation where y is not explicitly defined in terms of x.
- 🔍 The product rule is applied as f'g + fg' when differentiating a product of two functions, f and g.
- 🤔 To solve for dy/dx, algebraic manipulations such as subtraction and division are used to isolate the desired derivative.
- 📈 The concept of 'rate of change' in the context of a word problem typically indicates the need to find a derivative.
- 📊 When dealing with business-related problems, the cost is often a function of a quantity, and the rate of change of cost with respect to that quantity is found using differentiation.
- 🧮 For related rates problems, an equation relating the variables is first established, then differentiated with respect to time, and finally, algebra is used to solve for the desired rate.
- 🏗️ In the ladder-word problem, the Pythagorean theorem is used to relate the distance of the ladder from the wall and the height of the ladder above the ground.
- 🚢 For the ship-word problem, the relationship between distances is again established using the Pythagorean theorem, and rates of change are calculated based on the movement of the ships.
- 🎈 The rate of change of the radius of a spherical balloon is found by differentiating the volume-radius relationship with respect to time.
- 📉 The change in demand for a product, such as an Amazon subscription, can be calculated using the price-demand relationship and the rate at which the price is changing.
- ⚖️ Practice is emphasized as a key component of understanding and solving related rates and implicit differentiation problems, drawing an analogy to practicing free throws in basketball.
Q & A
What is the process of implicit differentiation?
-Implicit differentiation is a method used to find the derivative of an equation that does not explicitly express the dependent variable as a function of the independent variable. It involves differentiating both sides of an equation with respect to the independent variable, using the chain rule and product rule where necessary, and then solving for the derivative of the dependent variable.
How do you apply the product rule in differentiation?
-The product rule is applied when differentiating a product of two functions. If you have a function f(x) = g(x) * h(x), then the derivative f'(x) is given by g'(x) * h(x) + g(x) * h'(x), where g'(x) is the derivative of g and h'(x) is the derivative of h.
What is the relationship between the number of business cards and the cost according to the given transcript?
-The relationship between the number of business cards (n, in hundreds) and the cost (c, in dollars) is given by the equation 2(n + 3)^2 - c^2 = 9. This equation represents a mathematical relationship that determines the cost for a certain number of business cards.
How do you find the rate of change of the cost with respect to the number of business cards?
-To find the rate of change of the cost with respect to the number of business cards, you would differentiate the cost equation with respect to n (the number of business cards), which gives you the derivative dc/dn. You then solve for dc/dn and plug in the given values to find the specific rate of change.
What is the purpose of the related rates concept in calculus?
-The purpose of related rates in calculus is to solve problems involving the rates at which certain quantities are changing with respect to time. It is used to find an unknown rate of change given other related rates and the relationship between the quantities involved.
How do you solve a related rates problem?
-To solve a related rates problem, follow these steps: 1) Determine an equation that relates the two variables with respect to time. 2) Differentiate both sides of the equation with respect to time, using implicit differentiation. 3) Use algebra to rearrange the result to solve for the desired rate of change.
What is the application of implicit differentiation in related rates problems?
-Implicit differentiation is used in related rates problems to find the derivatives of the variables involved when the relationship between them is not explicitly given. It allows you to find the rate of change of one variable with respect to another when both are functions of time.
How do you find the rate at which the bottom of a ladder is moving away from a wall?
-To find the rate at which the bottom of a ladder is moving away from a wall, you would use the Pythagorean theorem to relate the horizontal distance (x), the vertical distance (y), and the length of the ladder (hypotenuse). Then, you would differentiate this relationship with respect to time to find dx/dt, the rate at which the bottom of the ladder is moving.
What is the formula for the volume of a sphere in terms of its radius?
-The formula for the volume (V) of a sphere in terms of its radius (r) is V = (4/3)πr^3. This formula is used to relate the volume and the radius of a sphere.
How do you find the rate at which the radius of a spherical balloon is increasing if air is being pumped in at a constant rate?
-To find the rate at which the radius of a spherical balloon is increasing, you would first relate the volume and the radius using the formula for the volume of a sphere. Then, you would differentiate this relationship with respect to time to find dr/dt, the rate of change of the radius with respect to time. Finally, you would plug in the given values to solve for dr/dt.
What is the impact on demand when Amazon increases the price of its Prime subscription at a constant rate?
-When Amazon increases the price of its Prime subscription at a constant rate, the demand for subscriptions is expected to decrease, as higher prices typically lead to lower demand. The rate of change in demand (dn/dt) can be found by differentiating the relationship between price and demand with respect to time and then solving for dn/dt using the given values.
Outlines
📚 Implicit Differentiation and Product Rule
The video begins with a quiz question about finding the derivative of y with respect to x when y is given implicitly. The instructor uses the product rule for differentiation, applying it to 5y^3 * ln(x), and then finds the derivative of x^2 with respect to x, which is 2x. By rearranging and simplifying the equation, the derivative dy/dx is found to be (2x - 5y^3/x) / (15y^2 * ln(x)). The problem is left unsolved for specific values of x and y, as they are not provided.
💳 Application Problem: Cost and Business Cards
The second question is an application problem involving the cost of printing business cards. The relationship between the number of business cards (n, in hundreds) and the cost (c) is given by a mathematical rule. The goal is to find the rate of change of the cost with respect to the number of business cards (dc/dn). Using the given equation, the derivative is taken with respect to n, and the resulting equation is solved for dc/dn. The final step involves plugging in n=1 to find the specific rate of change at that point, which is calculated to be $2.50 for 100 business cards.
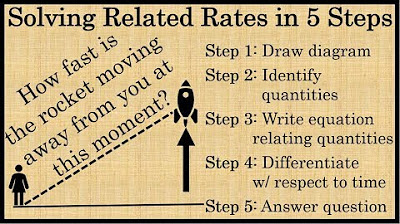
The third paragraph introduces related rates problems, which involve finding rates of change for variables that are functions of time. The instructor emphasizes the importance of implicit differentiation in solving these problems. A step-by-step approach is outlined: first, determine the relationship between the variables; second, take the derivative of this relationship with respect to time; and third, use algebra to solve for the desired rate. An example involving a ladder leaning against a wall is used to illustrate the process.
📐 Pythagorean Theorem in Related Rates
This paragraph continues the discussion on related rates, focusing on the application of the Pythagorean theorem. The scenario involves a ladder leaning against a wall, with the top of the ladder falling as time passes. Using the Pythagorean theorem to relate x (distance from the wall to the bottom of the ladder) and y (height of the ladder above the ground), the instructor demonstrates how to take the derivative with respect to time and solve for dx/dt, the rate at which the bottom of the ladder is moving across the ground.
🚢 Marine Navigation: Tanker and Barge
The sixth paragraph presents a nautical-themed related rates problem involving an oil tanker traveling west towards a lighthouse and a freight barge traveling north away from it. The goal is to find the rate of change of the distance between the two ships (dz/dt) when a certain distance is given for x and y (the distances from the lighthouse to the tanker and barge, respectively). The problem is solved using the Pythagorean theorem to relate x, y, and z, and then differentiating with respect to time to find the desired rate.
🎈 Inflatable Balloon and Its Radius
In the ninth paragraph, the problem involves a spherical balloon with air being pumped in at a rate of 25 cubic centimeters per second. The task is to find how fast the radius of the balloon is changing when the radius is 10 cm. The relationship between the volume (V) and radius (r) of a sphere is given, and the derivative of this relationship with respect to time is taken to find dr/dt, the rate of change of the radius.
📈 Amazon Prime Subscription Pricing
The tenth paragraph discusses a scenario where Amazon is increasing the price of its Prime subscription at a constant rate, and the goal is to determine how many customers Amazon expects to lose in the following month. The relationship between the price (P) and the number of subscriptions (n) is given, and the problem involves finding the rate of change of demand (dn/dt) with respect to time. The derivative of the given relationship with respect to time is taken, and the resulting equation is solved for dn/dt.
📉 Customer Loss Due to Price Increase
The eleventh paragraph provides a detailed solution to a problem where Amazon is increasing its subscription price and the focus is on calculating the expected customer loss. The relationship between price and demand is expressed through an equation, and the rate of price increase is represented as dp/dt. The problem is solved by differentiating the given equation with respect to time and solving for dn/dt, which represents the rate of customer loss per month.
Mindmap
Keywords
💡Implicit Differentiation
💡Product Rule
💡Derivative
💡Related Rates
💡Pythagorean Theorem
💡Rate of Change
💡Chain Rule
💡Business Cards Printing Cost
💡Amazon Prime Subscription
💡Spherical Balloon
💡Constant Rate of Change
Highlights
The transcript discusses the process of implicit differentiation, a technique used in calculus to find derivatives of equations that are not explicitly expressed.
The use of the product rule in differentiation is explained, which is crucial for handling expressions involving the multiplication of two functions.
An example of implicit differentiation is worked through, illustrating the step-by-step process to find the derivative of y with respect to x.
The concept of rate of change is introduced, which is synonymous with the derivative and is used to find how quickly a quantity is changing.
An application problem involving an online printing service's pricing model is solved using differentiation to find the rate of change in cost.
The relationship between the number of business cards printed and the cost is mathematically represented and then differentiated to find the rate of change.
The transcript demonstrates how to rearrange an equation algebraically to solve for a specific rate of change, which is key in applied mathematics problems.
Related rates problems are introduced, which involve using implicit differentiation to find the rate at which one quantity changes with respect to another.
An example of a related rates problem involving a ladder leaning against a wall is presented, showing how to use geometric relationships to set up and solve the problem.
The use of the Pythagorean theorem in setting up related rates problems is highlighted, as it is a common method for establishing relationships between variables.
The transcript emphasizes the importance of drawing diagrams to visualize and solve related rates and word problems in calculus.
The process of solving for a rate of change in a related rates problem involves three main steps: determining the relationship, taking the derivative with respect to time, and solving for the desired rate.
A maritime-themed word problem is solved, demonstrating how to use related rates to find the rate of change of the distance between two ships.
The transcript shows how to use algebraic manipulation to simplify expressions derived from implicit differentiation, which is essential for finding exact values.
The concept of rationalizing the denominator is explained, which is a technique used to eliminate the square root from the denominator of a fraction.
The transcript advises students to practice related rates problems on their own to prepare for exams, emphasizing the importance of active practice over passive observation.
Two additional examples of related rates problems are briefly mentioned, encouraging students to attempt them independently to reinforce learning.
The importance of understanding and applying the chain rule when differentiating more complex expressions is stressed, which is a fundamental skill in calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: