Intro to Related Rates
TLDRThe video script discusses the concept of related rates in mathematics, focusing on how the rates of change of different variables are interconnected. The presenter illustrates this with a word problem involving two cars traveling in perpendicular directions. Using the Pythagorean theorem, the script establishes a relationship between the distances traveled by the cars and their separation distance. The key insight is that by taking the derivative of this relationship with respect to time, one can determine the rate of change of the distance between the cars. The example concludes with calculating the rate of change as 78 miles per hour. The steps outlined for solving related rates problems include visualizing the scenario, finding an equation relating the variables, differentiating to find the rate, and then substituting specific values to solve for the rate of change.
Takeaways
- 📐 The concept of related rates in mathematics involves finding the relationship between the rates of change of different variables.
- 🚗 An example problem involves two cars traveling in perpendicular directions (east and north), and we are interested in how their distances relate over time.
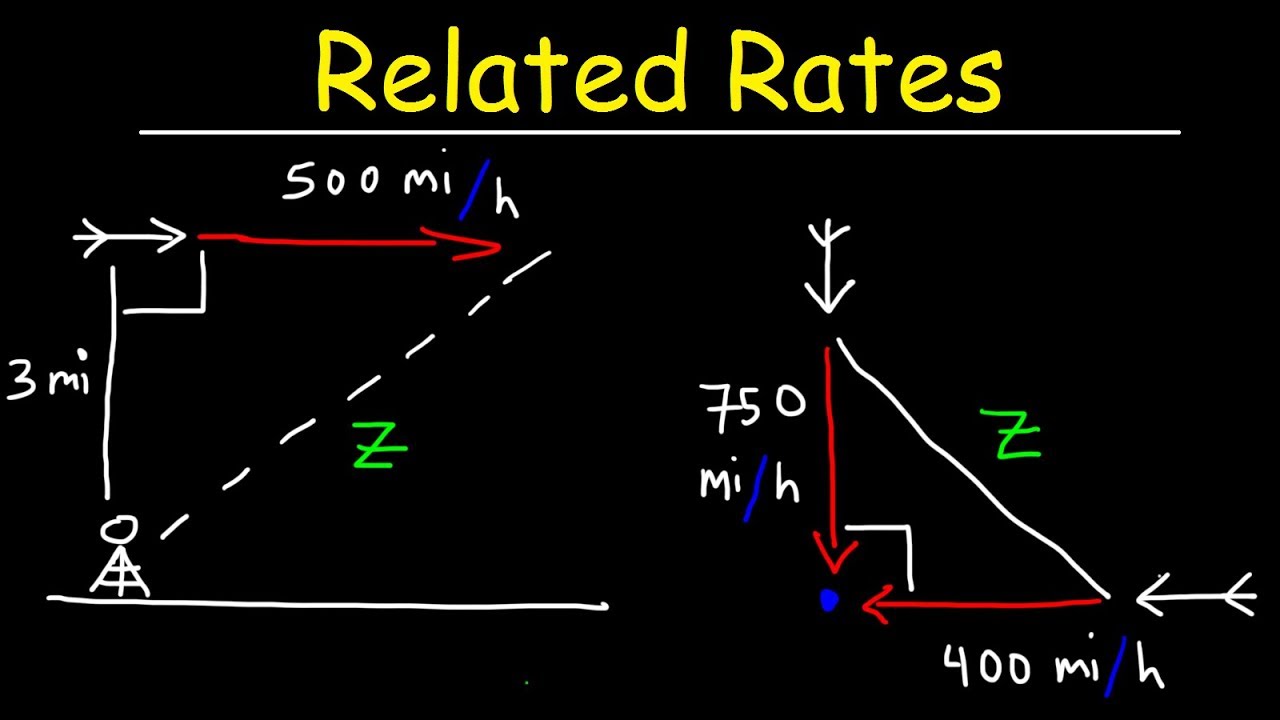
- 🔢 Using the Pythagorean theorem, the distance between the two cars can be expressed as the square root of the sum of the squares of their individual distances.
- ⏱️ The rates of change, or velocities, of the cars' positions are given as 60 mph for car A and 50 mph for car B.
- 🧮 By differentiating the Pythagorean equation with respect to time, we can establish a relationship between the rates of change of the distances (X' and Y') and the rate of change of the distance between the cars (D').
- 🔄 Applying the chain rule during differentiation leads to an equation that relates the original variables (X, Y, D) and their derivatives (X', Y', D').
- 🌐 The derivative of the distance with respect to time (D') can be found by rearranging the differentiated equation to solve for D' in terms of X', Y', and D.
- 📌 After substituting the given values, it is determined that the distance between the two cars is changing at a rate of 78 miles per hour.
- 📈 The process of solving related rates problems involves sketching a visual representation, finding a relationship equation, differentiating, and then substituting specific values to find rates of change.
- 📚 The steps for related rates problems are: understanding and visualizing the problem, finding a relationship equation, differentiating to find a rate relationship, and then calculating specific rates using given values.
- 🛣️ The final answer provides the rate of change of the distance between two objects with respect to time, which in this case is a measure of how quickly the distance is changing as the objects move along their respective paths.
Q & A
What is the concept of related rates in mathematics?
-The concept of related rates in mathematics involves finding the relationship between the rates of change of different variables, rather than the variables themselves. It's used to solve problems where the rate of change of one quantity is dependent on the rate of change of another.
What is the example problem discussed in the transcript?
-The example problem involves two cars, one driving east and the other north, starting from the same point. The task is to find the rate at which the distance between the two cars is changing over time, given their respective speeds.
How is the distance between the two cars initially calculated?
-The initial distance between the two cars is calculated using the Pythagorean theorem, where the distance squared (D^2) is equal to the sum of the squares of the distances each car has traveled (X^2 + Y^2), with X being 0.4 miles and Y being 0.3 miles, resulting in a distance of half a mile.
What are the speeds of the two cars in the example?
-The speed of car A traveling east is 60 miles per hour, and the speed of car B traveling north is 50 miles per hour.
How is the rate of change of distance between the two cars with respect to time found?
-The rate of change of distance (D') with respect to time is found by taking the derivative of the distance equation with respect to time, applying the chain rule and power rule, and then solving for D' using the given speeds of the cars.
What is the final calculated rate of change of the distance between the two cars?
-The final calculated rate of change of the distance between the two cars is 78 miles per hour.
What are the steps involved in solving related rates problems?
-The steps in solving related rates problems are: 1) Visualize the problem and sketch a picture, 2) Find an equation that relates the variables of interest, 3) Differentiate the equation to find a relationship between the rates of change, and 4) Plug in specific values to find the rate at a particular instant.
Why is it necessary to differentiate the original equation in related rates problems?
-Differentiating the original equation is necessary to find the relationship between the rates of change of the variables, which is the primary goal in related rates problems. This allows us to determine how one quantity is changing with respect to another.
What mathematical theorem is used to establish the initial relationship between the distances traveled by the cars and the distance between them?
-The Pythagorean theorem is used to establish the initial relationship between the distances traveled by the cars (X and Y) and the distance between them (D).
What is the chain rule in calculus, and how is it applied in this context?
-The chain rule is a method for finding the derivative of a composition of functions. In this context, it is applied when differentiating the distance equation with respect to time, allowing us to find the rates of change (X' and Y') of the distances traveled by the cars.
How does the concept of related rates apply to real-world scenarios?
-The concept of related rates is applicable to real-world scenarios where multiple quantities are changing simultaneously, and we are interested in understanding how the rate of change of one quantity is related to the rate of change of another. Examples include physics problems, engineering applications, and economic models.
What is the role of differentiation in related rates problems?
-Differentiation is used to find the rates of change (derivatives) of the variables in the original equation. This is crucial in related rates problems because it allows us to express the relationship between the variables in terms of their rates of change, which is the primary focus of such problems.
Outlines
📐 Understanding Related Rates in a Word Problem
The paragraph introduces the concept of related rates in mathematics, focusing on how variables change in relation to each other over time. It uses a word problem involving two cars driving in different directions to illustrate the concept. The paragraph describes how to set up an equation using the Pythagorean theorem to find the distance between the two cars and then how to differentiate this equation with respect to time to find the rate of change of distance. The key points include: identifying the variables, setting up the initial equation, differentiating the equation to find rates, and substituting given values to find the rate of change (D') which is 78 miles per hour in this example.
🔍 Steps to Solve Related Rates Problems
This paragraph outlines the steps to solve related rates problems. It emphasizes the importance of visualizing the problem, finding an equation that relates the variables of interest, differentiating this equation to find rates, and then using specific values to solve for the rate of change. The paragraph reiterates the process used in the previous example, highlighting the methodical approach to solving such problems. The steps include: sketching a visual representation of the problem, finding an equation that relates the variables, differentiating to find the rate of change, and finally calculating the rate at specific values to get a numerical answer.
Mindmap
Keywords
💡Equation of Multiple Variables
💡Related Rates
💡Word Problem
💡Pythagorean Relationship
💡Derivative
💡Chain Rule
💡Distance as a Function of Time
💡Velocity
💡Rate of Change
💡Differentiation
💡Calculus
Highlights
The concept of related rates in mathematics involves finding the relationship between the rates of change of different variables.
A specific example is given involving two cars traveling in different directions, with one going east and the other going north.
The distance between the two cars is represented using the Pythagorean theorem, with the equation D^2 = X^2 + Y^2.
The initial positions of the cars are given, with Car A having driven 0.4 miles east and Car B 0.3 miles north.
The distance between the cars at that specific time is calculated to be 0.5 miles.
The velocities of the two cars are provided, with Car A traveling at 60 mph and Car B at 50 mph.
The equation relating the distance D to time T is derived by differentiating the Pythagorean equation with respect to time.
The derivative of the distance with respect to time, D', is found to be (2X*X' + 2Y*Y') / D.
By rearranging the formula, the rate of change of distance D' can be expressed as (X'^2 + Y'^2) / D.
Plugging in the given values for X, Y, X', and Y', the rate of change of distance D' with respect to time is calculated to be 78 mph.
The major steps in solving related rate problems include visualizing the problem, finding an equation relating the variables, differentiating, and evaluating at specific values.
The process demonstrates how to compute the rate of change of a quantity, in this case the distance between two moving objects.
The example illustrates the practical application of related rates in determining how quantities change over time in real-world scenarios.
The use of derivatives is crucial in finding the rates of change and understanding how different quantities are interrelated.
The Pythagorean theorem is applied in a novel way to model the relationship between distances and velocities in a dynamic system.
The problem-solving approach involves both algebraic manipulation and geometric interpretation, showcasing the interconnectedness of mathematical concepts.
The final answer provides insight into the rate at which the distance between the two cars is changing over time.
The method can be generalized to other related rate problems involving different variables and rates of change.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: