Math1325 Lecture 11-4 - Related Rates

Michael Bailey

11 May 201615:59

EducationalLearning

32 Likes 10 Comments

TLDRThis lecture on Section 11.4, related rates, delves into the application of calculus to real-world problems involving changing quantities. The focus is on understanding how the rate of change of one variable, such as the volume of a balloon, is related to the rate of change of another, like the balloon's radius. The lecturer guides through the process of setting up equations that relate the variables, differentiating with respect to time, and solving for the unknown rate of change using calculus notation. Examples include calculating the rate at which a balloon's radius increases given the rate of volume change, and determining the rate of change of a tree's height based on the rate of change of its trunk radius. The lecture emphasizes the importance of using calculus notation, identifying given information, and practicing problems to solidify understanding of related rates in calculus.

Takeaways

📚 The lecture focuses on Section 11.4 related rates in calculus, which is a favorite section because it connects calculus notation to real-world applications.
🎈 An example of a related rates problem involves a spherical balloon where the volume and radius are changing at rates that are related to each other.
📐 To solve related rates problems, an equation that relates the two quantities is needed, followed by differentiation with respect to time.
🔢 The volume of a sphere is given by the formula V = (4/3)πR³, which is used to relate the volume and radius in the balloon example.
🤔 The motivation for related rates problems is to find the rate of change of one quantity in terms of another, which is often more easily measured.
🧮 Differentiation is performed using the chain rule, particularly when an explicit equation is not available, which is common in related rates problems.
📈 The rate of change of the volume of the balloon is given as 100 cubic centimeters per second, and the problem is to find dr/dt when the diameter is 50 cm.
📉 The concept of positive and negative rates of change is important; a positive rate indicates growth, while a negative rate indicates decrease.
🌳 Another example involves a tree's height being related to the radius of its trunk, with the formula H = 15R^(2/3), and the rate of change of the radius given as 3/4 in per year.
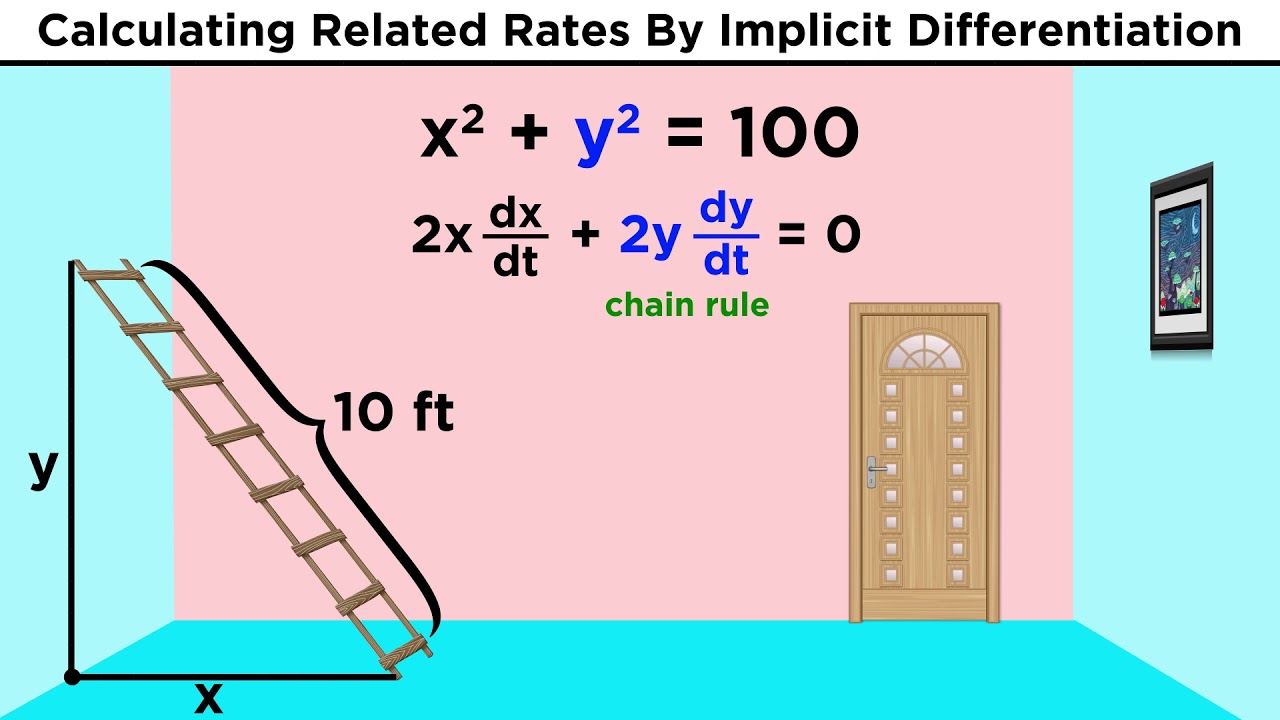
🪜 A ladder problem is presented, where the ladder's length, the rate at which it slides away from the wall, and the distance from the wall are used to find the rate at which the top of the ladder slides down.
📝 It is emphasized to use calculus notation for rates of change (e.g., dv/dt, dr/dt) to clearly communicate the mathematical operations being performed.
📚 Practice is key for mastering related rates problems, so students are encouraged to work through problems in homework and additional practice problems.

Q & A

What is the main concept behind related rates in calculus?
-The main concept behind related rates in calculus is to compute the rate of change of one quantity in terms of the rate of change of another quantity, which is usually more easily measured.
Why is it often easier to measure the rate of change of the volume rather than the radius in the context of a balloon being inflated?
-It is often easier to measure the rate of change of the volume because you can directly measure the amount of air going into the balloon, whereas measuring the radius increase requires more complex measurements around the circumference of the balloon.
What is the geometrical formula that relates the volume of a sphere to its radius?
-The geometrical formula that relates the volume (V) of a sphere to its radius (R) is V = (4/3)πR^3.
How is the chain rule used in the context of related rates problems?
-The chain rule is used in related rates problems to perform implicit differentiation when there isn't an explicit equation relating the variables. It helps to find the rate of change of one variable with respect to time in terms of another variable's rate of change.
What is the rate of change of the radius of a spherical balloon when the volume increases at a rate of 100 cubic centimeters per second and the diameter is 50 cm?
-The rate of change of the radius of the balloon with respect to time (dr/dt) is 0.127 cm/s when the diameter is 50 cm.
How is the height of a tree related to the radius of its trunk according to the given formula in the tree height problem?
-The height (H) of the tree is related to the radius (R) of its trunk by the formula H = 15R^(2/3).
What is the rate of change of the height of a tree when the radius of its trunk is increasing at a rate of 3/4 inch per year and the radius is 8 inches?
-The rate of change of the height of the tree with respect to time (dh/dt) is 3 and 3/4 feet per year when the radius is 8 inches.
How does the length of a ladder leaning against a wall relate to the rate at which its top is sliding down when the bottom slides away from the wall?
-The length of the ladder and the rate at which its top slides down the wall are related through the Pythagorean theorem, where the square of the ladder's length is equal to the sum of the squares of the horizontal and vertical distances from the wall.
What is the rate of change of the height at which the top of a 10-foot ladder is sliding down a wall when the bottom of the ladder is 6 feet away from the wall and sliding away at 1 foot per second?
-The rate of change of the height (dy/dt) is -3/4 feet per second under the given conditions.
Why is it important to consider the sign of the rate of change when solving related rates problems?
-The sign of the rate of change is important because it indicates whether the quantity is increasing (positive) or decreasing (negative) over time, which is crucial for accurately representing the physical situation being modeled.
What are some guidelines for solving related rates problems?
-Some guidelines for solving related rates problems include making a drawing to visualize the situation, labeling diagrams with known and given values, using calculus notation for rates of change, finding an equation that relates the variables, differentiating with respect to time, plugging in given values, and solving for the unknown rate of change.

Outlines

00:00

🎓 Introduction to Related Rates in Calculus

The lecturer begins by expressing enthusiasm for Section 11.4 on related rates, which is a favorite due to its practical application of calculus notation. The concept of related rates is introduced through an example involving the inflation of a spherical balloon. It is explained that as air is pumped into the balloon, both the volume and radius increase at related rates. The challenge is to express the rate of change of one quantity in terms of another, which is often more easily measured. The lecturer emphasizes the importance of using calculus notation for rates of change and introduces the formula for the volume of a sphere in relation to its radius.

05:00

📚 Solving Related Rates Problems with Spheres

The lecturer provides a detailed walkthrough of a problem involving a spherical balloon's volume increasing at a rate of 100 cubic centimeters per second. The goal is to find how fast the radius is increasing when the diameter is 50 cm. The process involves identifying given information, using calculus notation, and finding a formula that relates volume and radius. The volume of a sphere is derived from the geometrical formula and then differentiated with respect to time using the chain rule. By substituting the given values and solving the resulting equation, the rate of change of the radius with respect to time is found to be 0.127 cm/s. The importance of considering the sign of the derivative to determine whether a quantity is increasing or decreasing is also highlighted.

10:07

🌳 Applying Related Rates to Tree Growth

The next example involves a tree's height being related to the radius of its trunk. Given a formula that relates the height (H) to the radius (R) and a rate of change for R, the task is to find the rate of change for H when the radius is 8 inches. The lecturer demonstrates how to take the derivative of the given formula with respect to time and solve for the unknown rate of change (dh/dt) using the provided values. The solution process involves substituting the known values into the derived equation and solving for the rate of change, which is found to be 3 and 3/4 feet per year.

15:08

🪜 Solving a Ladder and Wall Problem Using Related Rates

The final example presented is a more complex problem involving a ladder leaning against a wall. The ladder's bottom slides away from the wall at a rate of 1 ft per second, and the challenge is to determine how fast the top of the ladder is sliding down when the bottom is 6 feet from the wall. The lecturer advises drawing a diagram to visualize the problem and labels the variables accordingly. Using the Pythagorean theorem and implicit differentiation, the rate of change for the height (dy/dt) as the bottom of the ladder moves away from the wall is calculated. The lecturer emphasizes the importance of units and ratios in related rates problems and provides a step-by-step guide to solving such problems, concluding with the solution of -3/4 feet per second.

📝 Conclusion and Advice for Related Rates Practice

The lecturer concludes the lecture on related rates by encouraging students to practice solving problems both in their homework and through additional problems listed in the syllabus. The importance of understanding how variables are related and differentiating with respect to time is reiterated. The lecturer advises using calculus notation for rates of change and emphasizes the need to solve for the unknown rate of change, which is typically the goal in related rates problems.

Mindmap

Keywords

💡Related Rates

Related rates are a method in calculus used to find the rate at which one quantity changes in relation to another. In the context of the video, this concept is used to solve problems where two or more variables are interrelated and changing over time. For instance, the video discusses how the volume and radius of a balloon change together as air is pumped into the balloon, demonstrating the application of related rates through the chain rule in calculus.

💡Derivative

The derivative represents the rate of change of a function with respect to a variable. In the video, derivatives like dv/dt and dr/dt are crucial in related rates problems to measure how fast one variable changes in relation to another over time. For example, dv/dt is used to find how fast the volume of the balloon is increasing as air is pumped into it.

💡Implicit Differentiation

Implicit differentiation is a technique to find the derivative of a function that is not explicitly solved for one variable in terms of another. The video uses this method to differentiate equations where variables like radius and volume are implicitly related, such as the volume formula for a sphere, to find the rate of change of the radius when the volume's rate of change is known.

💡Chain Rule

The chain rule is a formula to compute the derivative of a composite function. In the video, it is applied in the context of related rates problems to connect the derivatives of interdependent variables. For example, when deriving the relationship between the radius and volume of a sphere, the chain rule helps relate the time derivative of the radius to the time derivative of the volume.

💡Volume

Volume, in the context of the video, refers to the amount of space that an object occupies. It's particularly discussed in relation to a spherical balloon, where the volume increases as air is pumped in. The video explores how the volume's rate of change (dv/dt) can be used to find how fast the radius of the balloon increases.

💡Radius

Radius is the distance from the center to the edge of a circle or sphere. In the video, it's a central variable in the problem of a balloon being inflated, where the radius increases as the balloon fills with air. The concept is used to illustrate a practical application of related rates, calculating the rate of increase of the radius (dr/dt) as the balloon's volume expands.

💡Geometrical Equations

Geometrical equations relate geometric shapes' measurements, such as area, volume, and radius. The video references such equations, specifically the formula for the volume of a sphere, to establish relationships necessary for solving related rates problems involving shapes like balloons and spheres.

💡Rate of Change

Rate of change is a measure of how quickly a quantity changes over time. In the video, this concept is applied to both mathematical functions and real-world scenarios, like how fast the volume of a balloon or the height of a tree changes. Rates of change are quantified by derivatives in calculus, such as dv/dt for volume or dh/dt for height.

💡Diameter

Diameter is twice the radius of a circle or sphere and is a crucial measurement in the balloon example discussed in the video. It's used to determine the radius at a certain point in the problem, showing a practical use of basic geometric relationships in calculus problems.

💡Calculus Notation

Calculus notation, such as dv/dt or dr/dt, is used extensively in the video to denote derivatives and rates of change. This notation is fundamental in formulating and solving related rates problems, aiding in the clear communication of how variables are derived and related mathematically over time.

Highlights

Section 11.4 on related rates is a favorite section in calculus for its practical application of calculus notation.

Related rates problems involve computing the rate of change of one quantity in terms of another, often more easily measured quantity.

An example is given involving the volume and radius of a spherical balloon, illustrating the concept of related rates.

The volume of a sphere is related to its radius by the formula V = (4/3)πR^3, which is used in related rates problems.

Differentiation with respect to time is used to find the rate of change of quantities, using the chain rule for implicit differentiation.

For the spherical balloon example, the rate of increase of the radius (dr/dt) is calculated when the diameter is 50 cm.

The derivative of volume with respect to time (dV/dt) is given as 100 cubic cm per second in the balloon example.

The importance of using calculus notation for rates of change is emphasized for clarity in solving related rates problems.

A second example involves the height of a tree related to the radius of its trunk, with a formula H = 15R^(2/3).

The rate of change of the tree's height (dH/dt) is calculated based on the rate of change of the trunk radius (dR/dt).

A ladder leaning against a wall is used as a third example to demonstrate the concept of related rates in a practical scenario.

The Pythagorean theorem is applied to find the rate at which the top of the ladder slides down the wall as the bottom moves away.

Drawings and diagrams are recommended to visualize and solve related rates problems, especially in more complex scenarios.

The sign of the derivative indicates whether a quantity is increasing or decreasing, which is crucial for the correct interpretation of rates.

Units of measurement are important in related rates problems to ensure the rate of change is correctly understood and calculated.

Guidelines for solving related rates problems include making a drawing, labeling variables, writing an equation relating variables, differentiating, and plugging in values.

Practice is encouraged with homework and additional problems to master the concept of related rates in calculus.

Transcripts

Browse More Related Video

Related Rates

Related Rates in Calculus

Calculus 1: Related Rates (Video #17) | Math with Professor V

AP CALCULUS AB 2022 Exam Full Solution FRQ#4d

Related Rates - Conical Tank, Ladder Angle & Shadow Problem, Circle & Sphere - Calculus

Business Calculus - Math 1329 - Section 2.6 - Implicit Differentiation and Related Rates

Math1325 Lecture 11-4 - Related Rates

Takeaways

Q & A

What is the main concept behind related rates in calculus?

Why is it often easier to measure the rate of change of the volume rather than the radius in the context of a balloon being inflated?

What is the geometrical formula that relates the volume of a sphere to its radius?

How is the chain rule used in the context of related rates problems?

What is the rate of change of the radius of a spherical balloon when the volume increases at a rate of 100 cubic centimeters per second and the diameter is 50 cm?

How is the height of a tree related to the radius of its trunk according to the given formula in the tree height problem?

What is the rate of change of the height of a tree when the radius of its trunk is increasing at a rate of 3/4 inch per year and the radius is 8 inches?

How does the length of a ladder leaning against a wall relate to the rate at which its top is sliding down when the bottom slides away from the wall?

What is the rate of change of the height at which the top of a 10-foot ladder is sliding down a wall when the bottom of the ladder is 6 feet away from the wall and sliding away at 1 foot per second?

Why is it important to consider the sign of the rate of change when solving related rates problems?

What are some guidelines for solving related rates problems?