AutoIonization of Water, Ion Product Constant - Kw, Calculating H3O+, OH-, and pH Using Ice Tables
TLDRThis tutorial delves into solving problems related to the autoionization of water, focusing on calculating hydroxide and hydronium ion concentrations at different temperatures. It starts with finding hydroxide concentration given the hydronium ion concentration at 25°C, using the ion product constant of water (Kw). It then explores whether solutions are acidic, basic, or neutral based on hydronium ion concentration. The tutorial progresses to discuss the effect of temperature on Kw, demonstrating calculations at 50°C, and explaining the endothermic nature of water's autoionization. Finally, it tackles a challenge problem involving sodium hydroxide solution, using equilibrium concepts and the quadratic equation to find pH, illustrating the meticulous approach needed for accurate chemistry problem-solving.
Takeaways
- 📚 The autoionization of water involves the formation of hydronium (H3O+) and hydroxide (OH-) ions from the reaction of water with itself.
- 🌡️ The ion product constant of water (Kw) at 25°C is 1 × 10^-14, and it changes with temperature, being temperature-dependent.
- 🔄 Water is an amphoteric substance, meaning it can act as both an acid and a base in the autoionization process.
- 🧪 To calculate hydroxide concentration at 25°C, use the formula: [OH-] = Kw / [H3O+].
- 📈 The concentration of H3O+ can determine if a solution is acidic, basic, or neutral. If [H3O+] > 1 × 10^-7 M, it's acidic; if [H3O+] = 1 × 10^-7 M, it's neutral; if [H3O+] < 1 × 10^-7 M, it's basic.
- 🔢 At 50°C, the Kw constant for water is 5.5 × 10^-14, indicating that the autoionization of water increases with temperature.
- 🎯 The direction of the autoionization reaction shift (towards reactants or products) can be determined by comparing the reaction quotient (Q) with the equilibrium constant (K).
- 🥼 The pH of a solution is calculated as the negative logarithm (base 10) of the hydronium ion concentration.
- 🧪 In a sodium hydroxide (NaOH) solution, the hydroxide concentration is the sum of the concentration from NaOH dissociation and that from water autoionization.
- 🔄 The autoionization of water is an endothermic reaction, as evidenced by the increase in Kw with temperature rise, according to Le Chatelier's principle.
- 📊 Solving for the pH of a NaOH solution involves understanding the equilibrium shifts and using the quadratic formula to find the hydronium ion concentration.
- 🌟 The final pH calculation confirms the nature of the solution (acidic, basic, or neutral) and aligns with the initial concentration analysis.
Q & A
What is the autoionization of water and how does it result in the formation of ions?
-The autoionization of water is a process where water molecules react with themselves to form hydronium (H3O+) and hydroxide (OH-) ions. In this process, one water molecule acts as an acid by donating a proton, and another acts as a base by accepting the proton, resulting in the formation of the conjugate acid H3O+ and the conjugate base OH-.
What is the significance of the ion product constant (Kw) in the autoionization of water?
-The ion product constant (Kw) is a crucial parameter in the autoionization of water. It is the equilibrium constant for the reaction and is equal to the product of the concentrations of H3O+ and OH- ions. At 25 degrees Celsius, Kw is 1 x 10^-14. This value is temperature-dependent and changes with varying temperatures, which affects the concentrations of the ions in the equilibrium expression.
How do you calculate the concentration of hydroxide ions (OH-) at 25 degrees Celsius given the concentration of H3O+ ions?
-To calculate the concentration of hydroxide ions (OH-) at 25 degrees Celsius, you use the ion product constant (Kw) and divide it by the concentration of H3O+ ions. The formula is: [OH-] = Kw / [H3O+]. For example, if [H3O+] is 2 x 10^-6 M, then [OH-] would be calculated as 1 x 10^-14 / 2 x 10^-6, resulting in 5 x 10^-9 M.
How can you determine if a solution is acidic, basic, or neutral based on the concentration of H3O+ ions?
-At 25 degrees Celsius, if the concentration of H3O+ ions is greater than 1 x 10^-7 M, the solution is acidic. If the concentration equals 1 x 10^-7 M, the solution is neutral. If the concentration is less than 1 x 10^-7 M, the solution is basic.
What is the relationship between the autoionization of water and temperature?
-The autoionization of water is an endothermic process. As the temperature increases, the ion product constant (Kw) increases, indicating a shift in the equilibrium towards the products (ions). This results in a higher concentration of both H3O+ and OH- ions in the solution, enhancing the autoionization process.
How does the temperature affect the Kw constant for water?
-The Kw constant for water changes with temperature. For instance, at 25 degrees Celsius, Kw is 1 x 10^-14, but at 50 degrees Celsius, Kw is higher at 5.5 x 10^-14. This indicates that increasing temperature promotes the autoionization of water, leading to increased concentrations of both hydronium (H3O+) and hydroxide (OH-) ions in the solution.
What is the significance of Le Chatelier's principle in understanding the effect of temperature on the autoionization of water?
-Le Chatelier's principle states that if a dynamic equilibrium is disturbed by changing the conditions, the position of equilibrium moves to counteract the change. In the context of the autoionization of water, increasing temperature (for an endothermic reaction) shifts the equilibrium to the right, increasing the concentrations of H3O+ and OH- ions. Conversely, decreasing temperature would shift the equilibrium to the left, favoring the formation of water molecules from the ions.
How do you calculate the pH of a solution given the concentration of H3O+ ions?
-The pH of a solution is calculated using the formula pH = -log[H3O+]. You take the negative logarithm of the hydronium ion concentration to find the pH value. For example, if [H3O+] is 2.345 x 10^-7 M, the pH would be -log(2.345 x 10^-7), which equals 6.63.
What is the relationship between the concentrations of H3O+ and OH- ions in a solution at equilibrium?
-At equilibrium, the concentrations of H3O+ and OH- ions are equal in a neutral solution. This is because the product of their concentrations equals the ion product constant (Kw). If the concentration of H3O+ is greater than OH-, the solution is acidic, and if OH- is greater than H3O+, the solution is basic.
How do you determine the direction in which the autoionization reaction of water will shift when a strong base like NaOH is dissolved in water?
-When a strong base like NaOH is dissolved in water, it dissociates completely into Na+ and OH- ions. This increases the concentration of OH- ions significantly. To determine the direction of the shift, calculate the reaction quotient (Q) using the initial concentrations of H3O+ and OH-. If Q > Kw, the reaction shifts to the left to reduce the concentration of OH- (and increase H3O+), and if Q < Kw, it shifts to the right. In the case of NaOH, since the OH- concentration is artificially high, the reaction will shift to the left.
What is the quadratic equation method used for in the context of calculating pH in the presence of a strong base like NaOH?
-The quadratic equation method is used to solve for the unknown concentration variable when the reaction quotient (Q) is greater than the ion product constant (Kw), indicating a shift in the autoionization equilibrium to the left. This method helps in finding the new equilibrium concentrations of H3O+ and OH- ions when a strong base like NaOH is added to the solution.
How does the presence of a strong base like NaOH affect the calculation of pH in a solution?
-The presence of a strong base like NaOH complicates the pH calculation because it increases the concentration of OH- ions significantly. This cannot be ignored as it affects the equilibrium concentrations of H3O+ and OH- ions. The calculation must account for both the OH- concentration from the strong base and the autoionization of water. The reaction quotient (Q) is calculated using these new concentrations, and the direction of the equilibrium shift is determined. The quadratic equation is then used to find the new equilibrium concentrations before calculating the pH.
Outlines
🌊 Autoionization of Water and Calculation of Hydroxide Concentration
This paragraph introduces the concept of autoionization of water, explaining how water can react with itself to form hydronium (H3O+) and hydroxide (OH-) ions. It emphasizes the amphoteric nature of water and presents the equilibrium expression for the reaction, highlighting the ion product constant (Kw) at 25°C. The main goal is to calculate the hydroxide concentration given the hydronium concentration, using the value of Kw. The paragraph also discusses how to determine if a solution is acidic, basic, or neutral based on the concentrations of H3O+ and OH- ions. Additionally, it explores the temperature dependence of Kw and its implications for the autoionization process, concluding that the process is endothermic.
📊 ICE Table Analysis and pH Calculation at Different Temperatures
This paragraph delves into the use of an ICE (Initial, Change, Equilibrium) table to analyze the autoionization of water at 50°C, where the Kw constant is higher than at 25°C. It explains how to set up the table, how the reaction shifts in response to changes in temperature, and how to calculate the hydronium ion concentration using the ICE table. The paragraph then discusses the calculation of pH based on the hydronium ion concentration and introduces the concept of Le Chatelier's principle as it applies to endothermic and exothermic reactions. It concludes with a summary of how changes in temperature affect the equilibrium constant (K) and reaction direction.
🧪 Dissolution of Sodium Hydroxide and its Effect on pH
This paragraph presents a challenge problem involving the dissolution of sodium hydroxide (NaOH) in water and the resulting effect on hydroxide and hydronium ion concentrations. It clarifies that the hydroxide concentration is not simply the concentration of NaOH due to the autoionization of water. The paragraph explains how to set up an ICE table to determine the direction in which the reaction will shift and how to calculate the reaction quotient (Q) in relation to Kw. It emphasizes the importance of understanding the direction of the shift to correctly solve the problem and calculate the pH of the solution.
🔢 Quadratic Equation Solution for Hydroxide Concentration
This paragraph focuses on solving a quadratic equation to find the change in hydroxide and hydronium ion concentrations resulting from the dissolution of NaOH. It explains how to use the ICE table to determine the initial and equilibrium concentrations and how to set up the quadratic equation based on the product of H3O+ and OH- ions equaling Kw. The paragraph provides a step-by-step solution to the quadratic equation, leading to the calculation of the change in hydroxide concentration (x). It concludes with the calculation of the hydronium ion concentration at equilibrium and the verification of the results using the product of H3O+ and OH- ions to match Kw.
📈 Final pH Calculation and Confirmation of Basic Solution
In this paragraph, the final steps of the calculation are presented, including the determination of the hydronium ion concentration and the calculation of the solution's pH. The paragraph explains how to use the negative log of the hydronium ion concentration to find the pH and verifies the results by ensuring that the product of the calculated H3O+ and OH- concentrations equals the ion product constant (Kw). The paragraph concludes by confirming that the solution is basic due to the hydroxide ion concentration being greater than the hydronium ion concentration, resulting in a pH slightly above 7.
Mindmap
Keywords
💡Autoionization
💡Hydronium Ion (H3O+)
💡Hydroxide Ion (OH-)
💡Ion Product Constant of Water (Kw)
💡pH
💡Temperature Dependence
💡Amphoteric Substance
💡Equilibrium Expression
💡Le Chatelier's Principle
💡Conjugate Acid-Base Pair
💡Quadratic Equation
Highlights
The tutorial discusses solving problems related to the autoionization of water, a key concept in chemistry.
At 25 degrees Celsius, the concentration of hydroxide can be calculated using the ion product constant (Kw) and the hydronium ion concentration.
Water is an amphoteric substance, meaning it can act as both an acid and a base, which is central to understanding its autoionization.
The equilibrium expression for the autoionization of water does not include water in its liquid phase, simplifying the expression to just the ions involved.
The value of Kw changes with temperature, highlighting the temperature dependence of the autoionization process.
The concentration of hydroxide is calculated by dividing Kw by the hydronium ion concentration, demonstrating a fundamental calculation in aqueous chemistry.
The acidity or basicity of a solution can be determined by comparing the hydronium ion concentration to a reference value at a specified temperature.
The Kw constant for water at 50 degrees Celsius is different from that at 25 degrees Celsius, indicating how temperature affects the autoionization equilibrium.
An ice table is introduced as a tool to visualize the changes in ion concentrations during the autoionization process.
The pH of a solution is determined by the negative logarithm of the hydronium ion concentration, a fundamental concept in understanding acidity.
The autoionization of water is an endothermic reaction, as evidenced by the increase in Kw with temperature.
Le Chatelier's principle is applied to explain how temperature changes affect the direction of the autoionization reaction.
The tutorial presents a challenge problem involving the calculation of pH for a sodium hydroxide solution, showcasing the application of the concepts discussed.
The hydroxide concentration in a sodium hydroxide solution is not simply the concentration of NaOH due to the autoionization of water.
The reaction quotient (Q) is used to predict the direction in which the autoionization reaction will shift upon the addition of NaOH.
The tutorial demonstrates the use of a quadratic equation to solve for the hydronium ion concentration in a complex scenario.
The final pH calculation for the sodium hydroxide solution is shown to be slightly basic, illustrating the practical application of the concepts.
Transcripts
Browse More Related Video
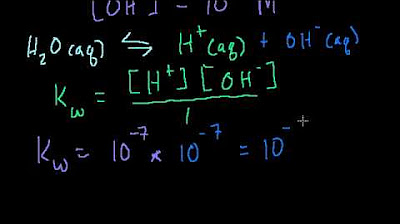
Introduction to pH, pOH, and pKw

pH, pOH, H3O+, OH-, Kw, Ka, Kb, pKa, and pKb Basic Calculations -Acids and Bases Chemistry Problems
pH and pOH: Crash Course Chemistry #30

Given pH & pOH, Solve for [H+] & [OH-] Practice Problems
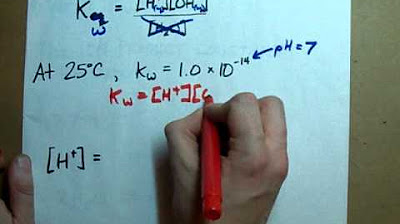
What is Kw (The Ion Product Constant of Water)

AQA A-Level Chemistry - Kw and Bases
5.0 / 5 (0 votes)
Thanks for rating: