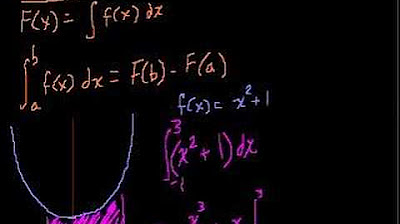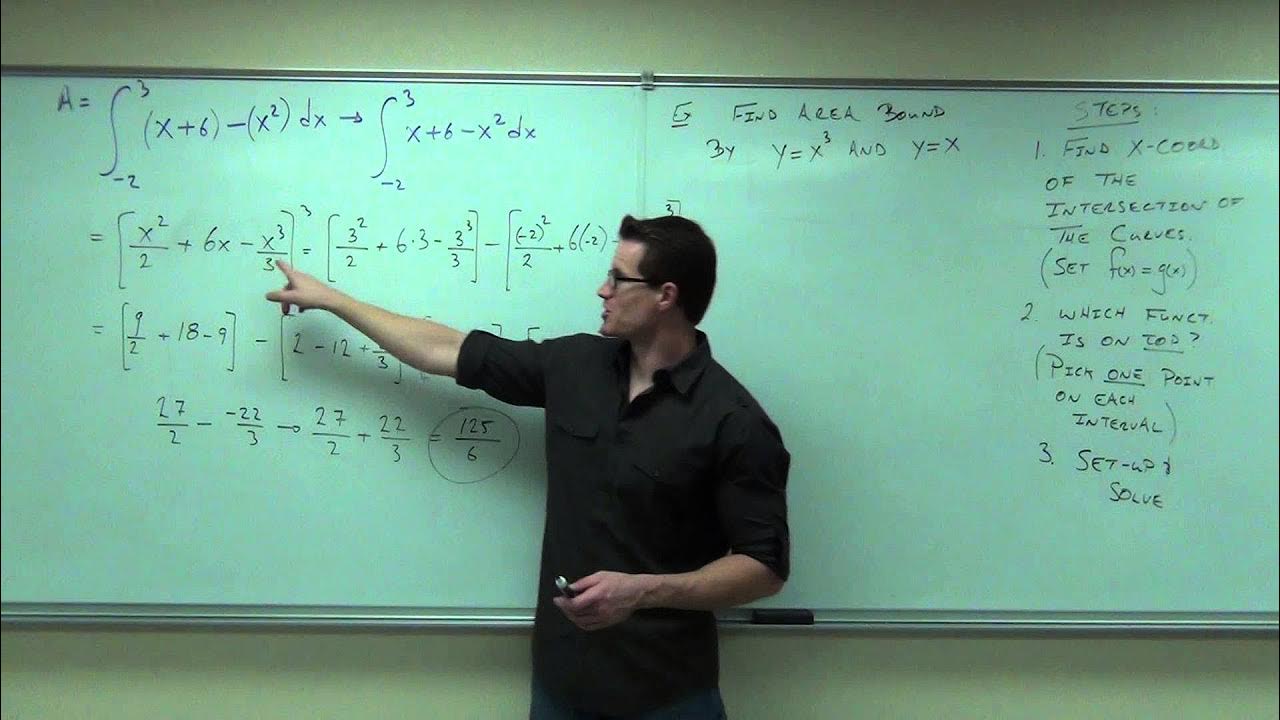Finding The Area Under The Curve Using Definite Integrals - Calculus
TLDRThis video script offers a comprehensive guide on calculating the area under curves using definite integrals. It begins with the foundational concept of integral calculus and progresses through various scenarios, including areas bounded by curves and the x-axis, as well as areas between two curves. The script meticulously details the steps and mathematical principles involved, such as setting up integrals, finding anti-derivatives, and evaluating them within given limits. The use of symmetry and the choice between integrating in terms of X or Y based on problem setup are also discussed. The video aims to enhance the viewer's understanding of integral calculus and its practical applications in solving area-related problems.
Takeaways
- 📌 The area under a curve can be found using the concept of definite integrals, which involves integrating the function from the starting point to the endpoint of the region.
- 📝 When dealing with a curve and the x-axis, the area is calculated using the integral of the function with respect to x (∫f(x)dx).
- 📝 If the area is bounded by a curve and another line (e.g., y=c), the area is found using the integral with respect to y (∫G(y)dy), where G(y) is the x-value function of the curve.
- 🔢 For the problem involving y=x^2 from x=0 to x=3, the area is calculated as the definite integral from 0 to 3 of x^2 dx, which evaluates to 9 square units.
- 📈 The process of finding the area bounded by a curve and a horizontal line (y=c) can involve finding x-intercepts and using the appropriate definite integral based on the function's form.
- 🤔 When a region is bounded by a line and a curve and the curve opens downward, the area is found by integrating from the lower x-intercept to the higher x-intercept.
- 🔢 For the parabola y=x^2 + 1 intersecting with y=4, the area is found by integrating from the x-intercept of y=4 (x=√3) to the x-intercept of y=x^2 + 1 (x=-1) with respect to y.
- 📊 When calculating the area between two curves, one method is to find the difference in the definite integrals of the two functions from a common interval.
- 📝 In cases where the region is below the x-axis, the area can be found by taking the negative of the integral from the left endpoint to the y-axis and adding it to the area found from the y-axis to the right endpoint.
- 📌 The choice between using x or y as the variable of integration depends on the problem setup and the symmetry of the region, with adjustments made for signs and limits of integration accordingly.
Q & A
What is the general formula for finding the area under a curve?
-The general formula for finding the area under a curve is the definite integral from point A to point B of the function f(x) dx.
How do you calculate the area bounded by a curve and the x-axis when the curve is y = f(x)?
-To calculate the area bounded by a curve y = f(x) and the x-axis, you find the definite integral from the leftmost to the rightmost point of the curve, substituting the function f(x) into the integral.
What is the key difference between calculating the area under a curve with respect to the x-axis and with respect to the y-axis?
-The key difference is that for the x-axis, you integrate with respect to x (definite integral from A to B of f(x) dx), while for the y-axis, you first express x in terms of y (x = g(y)), then integrate with respect to y (definite integral from C to D of g(y) dy).
What is the significance of finding the x-intercepts when calculating the area under a curve?
-Finding the x-intercepts is significant because they represent the limits of integration. They define the interval from which to calculate the definite integral to find the area bounded by the curve and the x-axis.
How do you find the area of a region bounded by the curve y = 4 - x^2 from x = 0 to x = 2?
-To find the area of the region bounded by y = 4 - x^2 from x = 0 to x = 2, you calculate the definite integral from 0 to 2 of (4 - x^2) dx. The anti-derivatives are 4x and (1/3)x^3, and by evaluating these from 0 to 2, you find the area to be 16/3 square units.
What is the process for calculating the area of a region bounded by a line and the x-axis over a symmetric interval?
-For a symmetric interval, you can calculate the area over one side (from 0 to the right x-intercept), then double the result to account for the mirrored area on the left side. Ensure to use a positive sign for regions above the x-axis and a negative sign for regions below the x-axis to obtain a positive area.
How do you calculate the area of a region bounded by the curve y = x^2 + 6x - 8 and the x-axis?
-First, find the x-intercepts by setting y to zero and factoring the quadratic equation. Then, calculate the definite integral from the leftmost to the rightmost x-intercept (from x = 2 to x = 4) of the function x^2 + 6x - 8. The area is the result of evaluating (-1/3)x^3 + 3x^2 - 8x from 2 to 4, which is 4/3 square units.
What is the method for finding the area of a region bounded by the curve y = 3x - x^2 from x = -2 to x = 3?
-You need to break this into two separate integrals due to the parabola opening downward and having both positive and negative areas. Calculate the absolute value of the area from -2 to 0 and add it to the area from 0 to 3. The total positive area is the absolute value of the area from -2 to 0 plus the area from 0 to 3.
How do you find the area of the shaded region bounded by the curves y = x^2 + 1 and y = 4?
-You can solve for x in the equation y = x^2 + 1 to express x in terms of y (x = sqrt(y - 1)), then use the integral from y = 1 to y = 4 of (sqrt(y) - 1) dy. Alternatively, find the x-intercept where y = 4 intersects with x^2 + 1, and calculate the definite integral from x = 0 to that x-intercept of (4 - (x^2 + 1)) dx.
What is the power rule for anti-differentiation in calculus?
-The power rule states that the anti-derivative of x^n, where n is any real number, is (1/(n+1))x^(n+1).
How do you handle negative areas when calculating the area under a curve?
-Negative areas occur when the region is below the x-axis. You can either double the area calculated for the positive region (if symmetric) or handle them separately by adding a negative sign to the integral (or subtracting the negative area from a positive area) to ensure the final answer is positive.
What is the importance of symmetry in calculating the area under a curve?
-Symmetry can simplify the process of calculating the area under a curve. If a curve is symmetric about the y-axis, you can calculate the area for one side and multiply by two to get the total area. If there's no symmetry, you must calculate each side separately and handle negative areas appropriately.
Outlines
📚 Introduction to Calculating Area under a Curve
This paragraph introduces the concept of finding the area under a curve using integral calculus. It explains the generic formula for calculating the area between a curve and the x-axis from points A to B, where the curve is represented by the function y = f(x). The importance of understanding the difference between the function y = f(x) and x = g(y) is emphasized, as it determines whether the area is calculated with respect to x or y. The paragraph also provides a step-by-step guide on how to sketch the curve and set up the integral for the specific problem of finding the area under y = x^2 from x = 0 to x = 3.
📈 Calculating Area Bounded by y = 4 - x^2
This paragraph focuses on calculating the area bounded by the curve y = 4 - x^2 from x = 0 to x = 2. It begins by drawing the curve and identifying the x-intercepts, which are -2 and 2. The integral formula for calculating the area is then applied, with the anti-derivatives of the function components being calculated and evaluated over the given interval. The process involves factoring the quadratic expression, integrating the function, and combining the results to find the area of the shaded region, which is determined to be 16/3 square units.
Mindmap
Keywords
💡Area
💡Definite Integral
💡Curve
💡Anti-derivative
💡Power Rule
💡Symmetry
💡X-intercepts
💡Y-intercepts
💡Parabolas
💡Integration
💡Limits of Integration
Highlights
Explaining the concept of finding the area under a curve using definite integrals.
Using the integral of a function to determine the area between the curve and the x-axis.
Discussing the power rule for anti-derivatives and how it applies to the problem.
Calculating the area bounded by the curve y = x^2 from x = 0 to x = 3.
Describing the process of shifting the parabola to find the x-intercepts for the curve y = 4 - x^2.
Integrating from 0 to 2 to find the area bounded by the curve y = 4 - x^2 and x-axis.
Exploring the concept of symmetry in integrals and how it simplifies the calculation.
Calculating the area of the region bounded by the line y = x from x = -4 to x = 4.
Discussing the importance of handling negative areas when the region is below the x-axis.
Finding the area bounded by the curve y = x^2 + 6x - 8 and the x-axis using x-intercepts.
Integrating from 2 to 4 to find the area of the region bounded by the curve y = x^2 + 6x - 8.
Describing the process of factoring quadratic equations to find x-intercepts.
Calculating the area of the region bounded by the curve y = 3x - x^2 from x = -2 to x = 3.
Using separate integrals to handle positive and negative areas for the region bounded by y = 3x - x^2.
Explaining how to calculate the area between two curves using integrals.
Solving for x in the equation y = x^2 + 1 to find the area between the curves using y-values.
Evaluating the integral from y = 1 to y = 4 to find the area of the shaded region between the curves.
Presenting two methods for calculating the area of the shaded region between two curves, in terms of either X or Y.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: