Probability Part 1: Rules and Patterns: Crash Course Statistics #13

CrashCourse
25 Apr 201812:00
EducationalLearning
32 Likes 10 Comments

TLDRIn this Crash Course episode on Statistics, Adriene Hill dives into the concept of pareidolia, illustrating our brain's tendency to recognize patterns, even in inanimate objects. She then transitions to a discussion on probability, distinguishing between empirical and theoretical probability through examples like slot machine odds and Skittle color chances. The episode further explores probability rules, including the addition and multiplication rules, and introduces notation for simplifying these concepts. Through engaging examples, such as the chances of encountering Cole Sprouse at IHOP or the implications of medical test accuracy, the video makes probability accessible and relevant, demonstrating its application in everyday decisions and scientific understanding.

Takeaways
  • 👁️ Pareidolia is a phenomenon where we recognize patterns, particularly faces, in inanimate objects due to our brain's pattern recognition capabilities.
  • 📈 There are two types of probability: empirical (based on actual data) and theoretical (an ideal or truth in the universe).
  • 🔮 Empirical probability provides a glimpse into the theoretical probability but may not always match due to sample uncertainty and randomness.
  • 🎲 Theoretical probability is considered an ideal truth that we attempt to estimate using data samples, such as calculating the odds of winning at a slot machine.
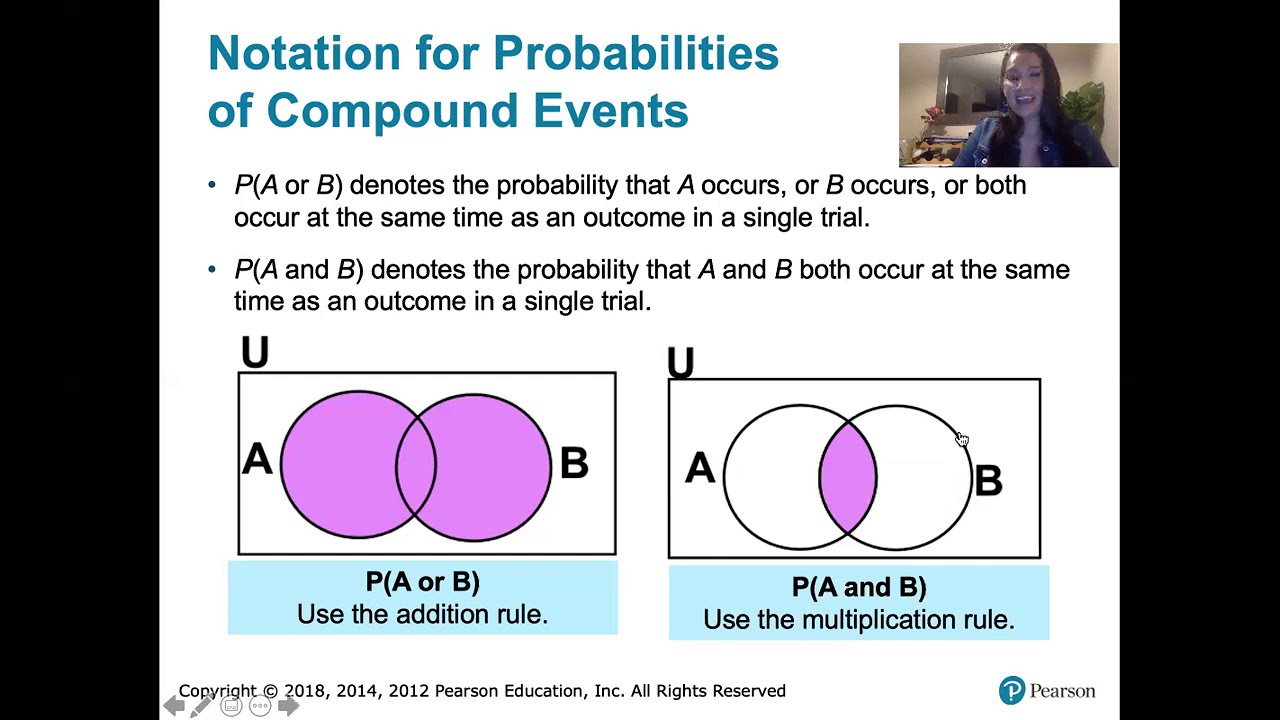
  • 🍭 The addition rule of probability helps calculate the chances of mutually exclusive events occurring, like picking specific colors from a Skittle bag.
  • 📊 Notation simplifies probability expressions, such as P(Red or Purple) to represent the combined probability of two events.
  • 🚫 Mutually exclusive events cannot happen at the same time, affecting how probabilities are calculated.
  • 📖 The multiplication rule assists in determining the likelihood of concurrent events, such as encountering a celebrity at a diner on a promotional night.
  • 📉 Conditional probabilities evaluate the chance of an event given another event has already occurred, essential in fields like medicine for understanding screening test implications.
  • 😷 Probability applies to real-life decisions and expectations, influencing daily choices and helping manage expectations about outcomes.
Q & A

  • What is pareidolia?

    -Pareidolia is when our brains see patterns like faces in inanimate objects, even when the patterns aren't really there. It happens because our brains are very good at recognizing patterns.

  • What are the two types of probability discussed?

    -The two types of probability discussed are empirical probability, which is based on actual observed data, and theoretical probability, which is the true underlying probability.

  • How do you calculate the probability of event A or event B happening?

    -To calculate the probability of event A or event B, use the addition rule: P(A or B) = P(A) + P(B) - P(A and B). This accounts for any outcomes where both events occur.

  • What is the multiplication rule used for?

    -The multiplication rule is used to calculate the probability of two or more independent events both occurring. You multiply the individual probabilities.

  • What does it mean for two events to be independent?

    -Two events are independent if the occurrence of one event does not affect the probability of the other event occurring. So the probabilities are unrelated.

  • What are conditional probabilities?

    -A conditional probability gives the probability of one event happening, given that another event has already occurred. It is written as P(A | B), the probability of A given B.

  • What is the difference between false positives and false negatives?

    -A false positive is when a test says something is abnormal but it's not. A false negative is when a test says everything is normal but something is actually abnormal.

  • How can probability help in everyday life?

    -Probability can help set reasonable expectations in uncertain situations, like getting tickets to an event or catching red lights when driving. It provides context on how likely outcomes are.

  • What was the key message of the video?

    -The key message was that probability helps us quantify uncertainty and set reasonable expectations. Even if we don't always have precise probabilities, thinking in terms of likelihood is useful.

  • What is the difference between P(A|B) and P(B|A)?

    -P(A|B) gives the probability of A occurring given that B has occurred. P(B|A) gives the probability of B occurring given that A has occurred. They are not always equal.

Outlines
00:00
🧠 Understanding Probability through Patterns

This section introduces the concept of pareidolia, where humans recognize faces in inanimate objects, as a segue into the broader topic of pattern recognition and probability. Adriene Hill explains the difference between empirical and theoretical probability using accessible examples. Empirical probability is derived from actual data and comes with a degree of uncertainty, whereas theoretical probability is an ideal or truth existing in the universe. Through examples like the slot machine and Skittles colors, the segment elaborates on calculating probabilities of single and multiple events, introducing the addition rule of probability for mutually exclusive events and the importance of empirical data in estimating theoretical probabilities.

05:04
🍦 The Multiplication Rule and Conditional Probabilities

This segment delves into the multiplication rule of probability with a hypothetical scenario involving actor Cole Sprouse and a local IHOP's 'Free Ice Cream Night'. It explains how to calculate the probability of two independent events occurring simultaneously, like seeing Cole at IHOP and it being Free Ice Cream Night, resulting in a 2% chance. Additionally, it covers the addition rule for calculating the probability of either event happening. The concept of independent and conditional probabilities is further explored, particularly how they apply to real-world situations like medical screenings for cervical cancer, illustrating the use of conditional probabilities in assessing the likelihood of a condition given a positive test result.

10:05
📚 Applying Probability to Everyday Decisions

The final segment highlights the challenges of assigning specific probabilities to daily occurrences, such as a teacher calling in sick or catching all red lights en route to school. It emphasizes that while calculating probabilities for everyday situations may not always be feasible, understanding and applying probability concepts is valuable for making informed decisions. Examples include choosing entertainment options with a higher probability of satisfaction, understanding the importance of flexibility in achieving goals (like seeing a popular movie), and making strategic choices based on probabilities (such as college applications or health risks). The segment encourages viewers to integrate probability thinking into their daily lives to better navigate uncertainties.

Mindmap
Keywords
💡Pareidolia
Pareidolia is a psychological phenomenon where the brain perceives recognizable patterns, especially faces, in unrelated and random stimuli, such as objects or surfaces. In the video, it's used as an opening example to illustrate how humans are pattern-seeking creatures, primed to recognize patterns even when they're not intentional or meaningful. This concept introduces the viewer to the idea that our brains are constantly looking for patterns, setting the stage for a discussion on probability and how we interpret patterns in data and events around us.
💡Probability
Probability is a fundamental concept in statistics, representing the likelihood of an event occurring. The video distinguishes between everyday use of the term and its statistical meaning, further dividing it into empirical and theoretical probability. Empirical probability is derived from actual data observations, while theoretical probability refers to the inherent likelihood of an event based on all possible outcomes. The video uses these concepts to explore how statisticians estimate the chances of various events, such as winning a jackpot or selecting a specific colored Skittle from a bag.
💡Empirical Probability
Empirical probability is defined in the video as the probability calculated from direct observations or experiments. It represents an estimation of the theoretical probability but can be subject to uncertainty due to the randomness and limited scope of samples. An example given is determining the ratio of girls in families based on observed data, illustrating how empirical probability gives insight into real-world occurrences and serves as an approximation of the true, theoretical probability.
💡Theoretical Probability
Theoretical probability is described as an ideal or 'truth' existing in the universe, which we aim to understand or estimate through statistical means. It is not directly observable but is inferred from patterns in empirical data. The video explains this concept using the example of playing a slot machine to estimate the jackpot's win probability, highlighting how theoretical probability underpins our understanding of chances in a perfect, controlled environment.
💡Mutually Exclusive
Mutually exclusive events are those that cannot happen at the same time. The video uses the example of picking a Skittle to explain that a Skittle cannot be both red and purple simultaneously, demonstrating the concept of mutually exclusive events in probability. This concept is crucial for understanding how to calculate the probability of either of two such events occurring, using the addition rule for mutually exclusive events.
💡Addition Rule
The addition rule of probability is used to calculate the likelihood of either of two events happening when those events are mutually exclusive. The video illustrates this with the probability of selecting either a red or purple Skittle, showing that you add the individual probabilities of each event occurring. This rule is foundational for understanding how to combine probabilities in scenarios where multiple outcomes are possible but do not overlap.
💡Independent Events
Independent events are those whose occurrence does not affect the likelihood of another event occurring. The video exemplifies this with the scenario of Cole Sprouse's visits to IHOP and 'Free Ice Cream Night,' explaining that these events do not influence each other. This concept is key to understanding how to calculate the probability of two events happening simultaneously using the multiplication rule, as it shows that the occurrence of one event does not change the probability of the other.
💡Conditional Probability
Conditional probability is the likelihood of an event occurring, given that another event has already happened. The video discusses this in the context of medical screenings and false positives/negatives, showing how conditional probabilities can inform decisions and interpretations in complex scenarios. It emphasizes the importance of understanding the relationship between events, particularly in assessing risks and making informed predictions.
💡Multiplication Rule
The multiplication rule helps calculate the probability of two or more independent events happening at the same time. The video uses the example of encountering Cole Sprouse at IHOP on 'Free Ice Cream Night' to demonstrate this concept. By multiplying the probabilities of each independent event, we can find the overall likelihood of both occurring together, showcasing how probabilities combine in scenarios involving sequential or concurrent events.
💡False Positive/Negative
False positives and negatives are errors in test results where a positive or negative outcome incorrectly indicates the presence or absence of a condition. The video uses cervical cancer screenings as an example to explain how these errors affect the interpretation of conditional probabilities. Understanding false positives and negatives is crucial in medical testing, risk assessment, and decision-making processes, highlighting the practical implications of probability in real-world scenarios.
Highlights

The introduction provides helpful context and background on the topic

The methods section clearly explains the experimental design and procedures

Key results are summarized in an easy to understand way

Limitations of the study are acknowledged transparently

The discussion meaningfully interprets the main findings

Connections are made between results and prior research

The implications of the research are considered thoughtfully

The conclusion summarizes the main points cohesively

The writing is clear, concise and easy to follow

The overall structure is logical and flows well

Tables and figures are used effectively

References are up-to-date and relevant

The work provides a significant contribution

There is potential for impactful applications

The research opens up promising new directions

Transcripts

Browse More Related Video

4.2.1 Addition and Multiplication Rules - Simple and Compound Events, and Their Probabilities

Multiplication & Addition Rule - Probability - Mutually Exclusive & Independent Events

Elementary Stats Lesson #7

Chi-Square Tests: Crash Course Statistics #29

AP Stats Test Quick Review: Probability

Statistics Lecture 4.2: Introduction to Probability

Rate This

5.0 / 5 (0 votes)

Thanks for rating: