Definite Integrals!
TLDRThe video script delves into the concept of definite integrals, a fundamental topic in calculus, which is closely related to the calculation of areas under curves. The presenter begins by illustrating how definite integrals can be used to find the area under a curve, using the example of a function represented in red. The script then defines the definite integral for non-negative, continuous functions over a closed interval [a, b], explaining that it represents the area bounded by the function, the x-axis, and the vertical lines x=a and x=b. The Fundamental Theorem of Calculus is introduced as the primary method for evaluating definite integrals, which involves finding an antiderivative of the function and subtracting its value at the lower limit from its value at the upper limit. The script proceeds with several examples, demonstrating how to apply the theorem and handle various types of integrals, including those requiring substitution (u-substitution). It also touches on the broader application of definite integrals in the context of accumulation, such as calculating total revenue from a marginal revenue function. The summary emphasizes the importance of understanding the process of finding antiderivatives and applying the Fundamental Theorem of Calculus to evaluate definite integrals, which are not only used for area calculations but also for a wide range of applications involving accumulation.
Takeaways
- 📐 **Definite Integrals and Area**: Definite integrals are used to calculate the area under a curve between two points, which can be visualized as the shaded region bounded by the function, the x-axis, and two vertical lines.
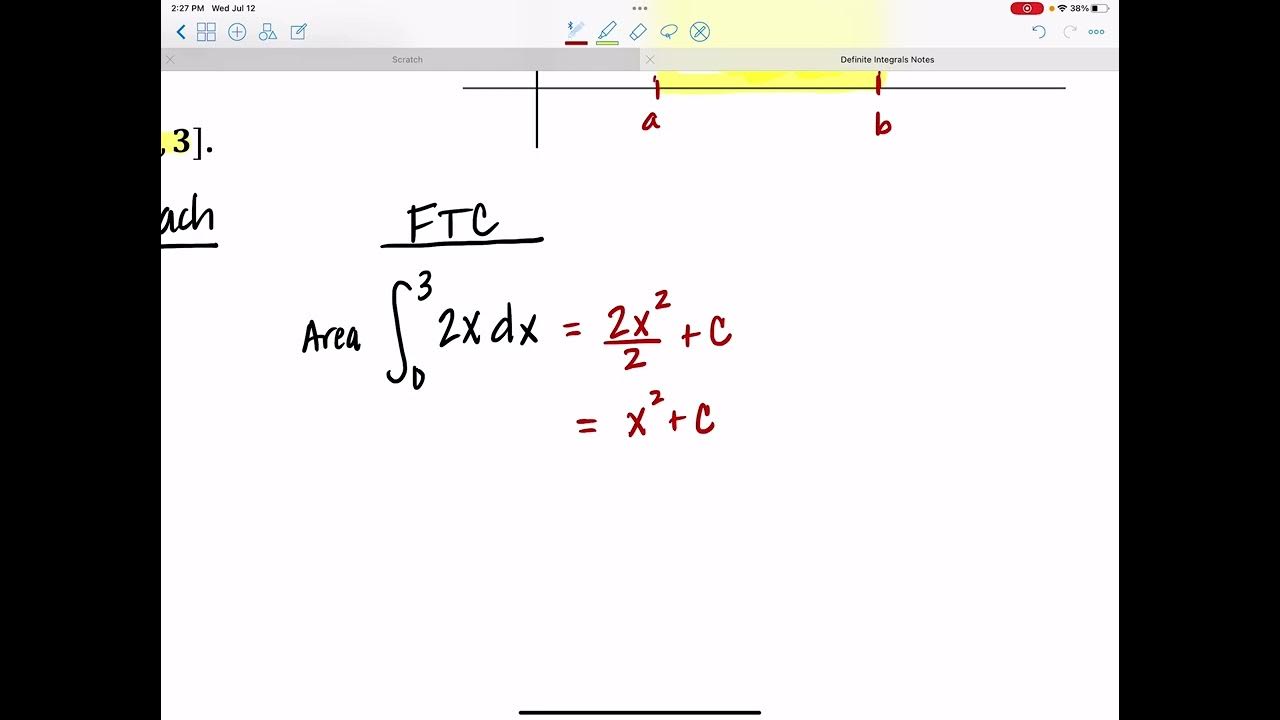
- 🌟 **Fundamental Theorem of Calculus**: The definite integral from A to B of a non-negative function f(x) is equal to the antiderivative F(x) evaluated at B minus the antiderivative evaluated at A (F(B) - F(A)).
- 📈 **Antiderivative and Evaluation**: To find a definite integral, first find the antiderivative of the function, then evaluate it at the upper and lower limits of integration and subtract.
- ⛰ **Right Triangle Rule**: For simple shapes like triangles, the area under the curve can be calculated using basic geometric formulas, but the definite integral provides a method for more complex shapes.
- 🔢 **Numerical Results**: Definite integrals yield numerical results, not functions, which represent the accumulated quantity, such as area or total revenue, between the points of integration.
- 🏗️ **Building Intuitive Understanding**: Understanding definite integrals as a process for accumulation helps in grasping the concept beyond just calculating areas.
- 📉 **Non-Negative Functions**: The process of finding definite integrals is straightforward for non-negative functions, which are those that are above the x-axis or on the x-axis.
- 🔄 **U-Substitution**: When a function cannot be integrated using basic rules, u-substitution can be a powerful technique, requiring the bounds of integration to be expressed in terms of the new variable u.
- 🧮 **Logarithmic and Exponential Functions**: Definite integrals can handle complex functions involving logarithms and exponents, which are evaluated using the rules of integration.
- 💰 **Application in Business**: Definite integrals are not only for areas; they are also used in business and economics to calculate total costs, revenues, and profits by integrating marginal functions over a range.
- ➗ **Cancellation of Constants**: In definite integrals, constants like C from the antiderivative are often omitted since they cancel out during the evaluation process.
Q & A
What is the fundamental theorem of calculus used for in the context of definite integrals?
-The fundamental theorem of calculus is used to evaluate definite integrals by relating them to antiderivatives. It states that the definite integral from A to B of a function f(x) is equal to the antiderivative F(x) evaluated at B minus the antiderivative evaluated at A.
How does the definite integral relate to the area under a curve?
-The definite integral from A to B of a non-negative function f(x) represents the area of the region bounded by the curve of f(x), the vertical lines x=A and x=B, and the x-axis.
What is the process to find the area under a curve using definite integrals?
-To find the area under a curve using definite integrals, you first identify the function and the interval over which you want to find the area. Then you integrate the function over that interval, and the result is the area under the curve between the specified limits.
Why is it common practice to omit the constant of integration (C) when dealing with definite integrals?
-The constant of integration (C) is often omitted in definite integrals because it cancels out when you subtract the antiderivative evaluated at the lower limit from the antiderivative evaluated at the upper limit, as per the fundamental theorem of calculus.
How can definite integrals be used to calculate total revenue in business?
-In business, definite integrals can be used to calculate total revenue by integrating the marginal revenue function over a specific interval of production or sales units. The result gives the total revenue accumulated from the lower to the upper limit of the interval.
What is the role of substitution (u-substitution) in evaluating definite integrals?
-U-substitution is a technique used to simplify the process of evaluating definite integrals, especially when the integral does not fit basic integration rules. By substituting a new variable (u) for a more manageable expression, the integral can often be transformed into a form that is easier to integrate.
What is the significance of the expression 'indefinite integrals' in the context of definite integrals?
-An indefinite integral represents the antiderivative of a function, which is a family of functions that differ by a constant. Definite integrals use the values of the indefinite integral at specific limits to calculate the accumulated value, such as area or total revenue, over an interval.
How does the definite integral generalize the concept of finding areas to the concept of accumulation?
-While definite integrals are often introduced in the context of finding areas under curves, they can also be used to calculate accumulated values of various quantities, such as total cost, revenue, or profit, over an interval. This makes the concept of definite integrals more versatile and applicable in various fields.
What is the correct setup for using the fundamental theorem of calculus to evaluate a definite integral?
-To use the fundamental theorem of calculus, you first find the antiderivative (indefinite integral) of the function you are integrating. Then, you evaluate this antiderivative at the upper limit of integration and subtract the value of the antiderivative at the lower limit of integration.
What is the difference between the area under a non-negative curve and the area under a curve that changes sign within the interval of integration?
-The area under a non-negative curve is given directly by the definite integral of the curve over the interval. However, if the curve changes sign within the interval, the definite integral represents the net area, which could be positive, negative, or zero, depending on how much of the curve is above versus below the x-axis.
How can you check if a function is non-negative over an interval for the purpose of using definite integrals to find areas?
-You can check if a function is non-negative over an interval by graphing the function and observing that it stays above the x-axis throughout the interval, or by using a graphing calculator to verify that the function values are all positive or zero.
What is the process of finding the antiderivative of a function?
-Finding the antiderivative, or indefinite integral, of a function involves reversing the derivative process. This is done by applying integration rules, such as power rules, trigonometric integrals, and logarithmic integrals, to find a function whose derivative is the original function.
Outlines
📐 Introduction to Definite Integrals
This segment introduces the concept of definite integrals as a method for calculating the area under a curve, which might initially seem daunting. The speaker explains that if the function f(x) is non-negative and continuous over a closed interval [a, b], the integral of f(x) from A to B defines the area enclosed by the graph of the function, the x-axis, and vertical lines at x = a and x = b. A practical example is provided using the linear function y = 3/2x, demonstrating the calculation of the area of a right triangle formed beneath the curve from x = 0 to x = 2, highlighting the integral's connection to simple geometric areas.
📘 Calculating Integrals Using Antiderivatives
The focus shifts to a deeper understanding of computing definite integrals via antiderivatives, guided by the Fundamental Theorem of Calculus. The theorem links the definite integral of a function over an interval to the difference in the values of its antiderivative at the endpoints of the interval. The explanation includes calculating the integral of the function 3/2 x from 0 to 2 by finding its antiderivative and evaluating it at the boundaries, reinforcing the concept with algebraic manipulations like breaking down x squared plus 4 over x into simpler expressions, thus demonstrating how to apply integration techniques to more complex functions.
🔍 Advanced Integration Examples
This section walks through more intricate examples of definite integrals, explaining their calculations and the simplification processes involved. It discusses integrating functions like x squared plus 4 over x from 1 to 4, utilizing algebraic simplifications for integration. Furthermore, the segment covers the use of the Fundamental Theorem of Calculus to calculate the integral of 6 times the square root of x plus x from 1 to 3, emphasizing the transformation of the function into a form suitable for straightforward integration and the calculation process of deriving a numerical answer.
🧮 Extension of Integral Calculations and Use Substitution
The narrative expands on the process of using substitution to solve integrals when the function or bounds complicate direct integration. It elucidates the change of variables technique, where bounds are adjusted according to the substitution variable 'u'. An example includes integrating x divided by 1 plus 4x squared from 0 to 2, detailing how to convert the bounds into terms of u and solve the integral in its new form. The explanation aims to clarify how substitution affects the integral's limits and the necessary steps to compute the integral after the transformation.
📉 Integration in Context: Practical Application Examples
This segment illustrates the application of definite integrals beyond theoretical mathematics, using examples that demonstrate accumulation functions in economics. A scenario is presented where a definite integral calculates total revenue generated over a range of units, starting with a marginal revenue function. The integration process shows how accumulation functions like total cost, profit, and revenue are derived from marginal rates using integrals. The practicality of these mathematical tools in real-world applications is underscored, offering insights into their significance beyond abstract concepts.
🚀 Conclusion and Recap of Definite Integrals
The concluding part summarizes the essential aspects of definite integrals explored throughout the video. It reinforces the understanding that definite integrals are not only about calculating areas but also serve as a fundamental tool in the accumulation of values, as seen in various practical examples. The speaker encourages further practice with homework and offers support through communication, ensuring students are comfortable with the material discussed and emphasizing the integral's role in broader mathematical and applied contexts.
Mindmap
Keywords
💡Definite Integral
💡Antiderivative
💡Fundamental Theorem of Calculus
💡Non-negative Function
💡Area under a Curve
💡Integration by Substitution (u-sub)
💡Marginal and Total Cost/Revenue/Profit
💡Continuous Function
💡Natural Logarithm
💡Evaluation Bar
💡Accumulation
Highlights
The definite integral is intimately connected with the concept of area and can be used to find the area under a curve.
If a function f(x) is non-negative and continuous on a closed interval [a, b], the definite integral from a to b represents the area bounded by the function and the x-axis.
The area under a curve can be calculated using the integral of the function with respect to x from the left endpoint to the right endpoint.
The Fundamental Theorem of Calculus provides a method for evaluating definite integrals by finding an antiderivative and subtracting its values at the endpoints.
The constant of integration (C) is typically omitted when calculating definite integrals as it cancels out in the evaluation.
Definite integrals can be used to calculate areas under non-negative curves, but they also have broader applications in accumulation, such as total revenue or cost.
The process of evaluating a definite integral involves finding an antiderivative, applying the fundamental theorem of calculus, and simplifying the result to a numerical value.
When using substitution (u-substitution) to solve a definite integral, it's necessary to express the bounds of integration in terms of the substitution variable.
Definite integrals can yield negative numbers, indicating accumulation in a different context, such as net loss rather than area.
The concept of accumulation is central to the broader application of definite integrals beyond just calculating areas.
In business applications, definite integrals can be used to find total costs, revenues, or profits by integrating marginal functions over a given interval.
The process of u-substitution requires algebraic manipulation and changing the bounds of integration to match the new variable.
When performing u-substitution, the original bounds of integration must be translated into the new variable's terms by substituting the values of x into the new variable's expression.
Definite integrals are evaluated by plugging the upper and lower bounds into the antiderivative and subtracting the results, yielding a numerical answer.
The total revenue accumulated over a range of production can be found by integrating the marginal revenue function over that range.
Definite integrals are not limited to geometric applications; they are a powerful tool for quantifying accumulation in various contexts, including economics and physics.
Practicing finding antiderivatives and applying the fundamental theorem of calculus is key to mastering the calculation of definite integrals.
Transcripts
Browse More Related Video
Definite Integrals
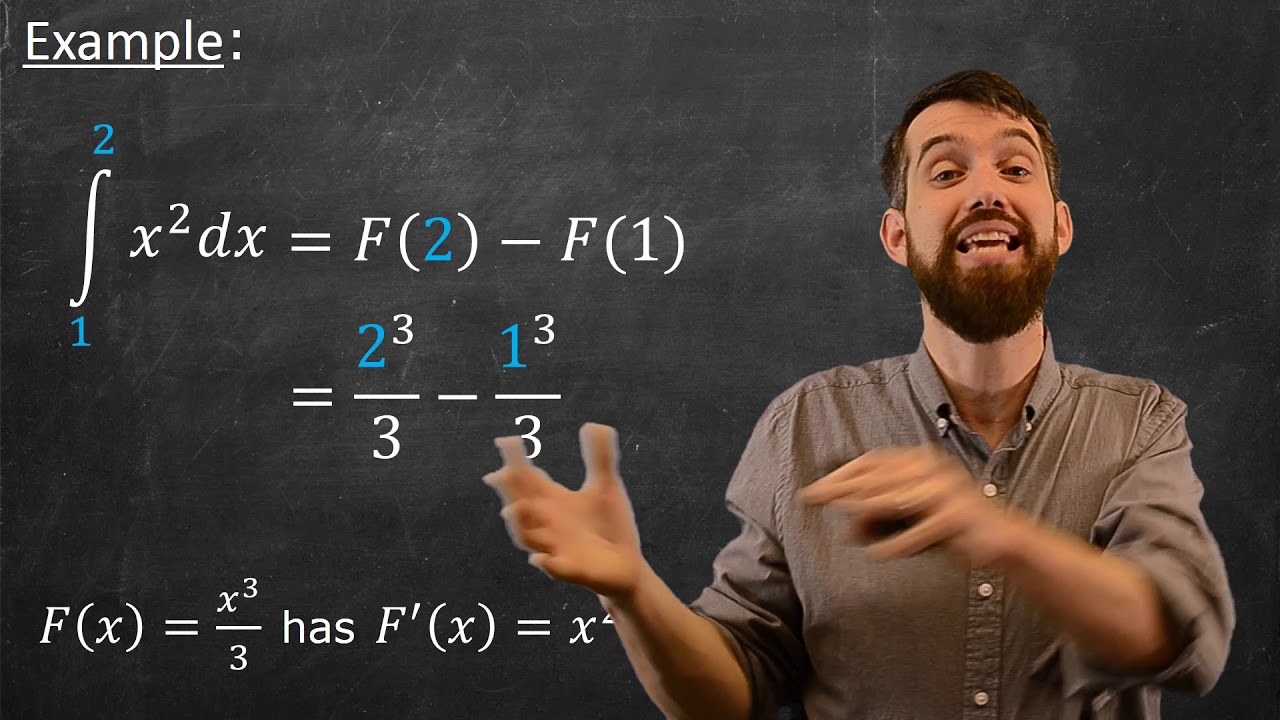
Fundamental Theorem of Calculus II

Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

Area between a curve and the x-axis | AP Calculus AB | Khan Academy
Math 11 - Section 4.3

Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy
5.0 / 5 (0 votes)
Thanks for rating: