Calculus AB Homework 7.3 Area Between Curves
TLDRThis video tutorial guides viewers through solving calculus problems involving the area between curves. It covers various methods, including vertical and horizontal cross-sections, and demonstrates the process of setting up and evaluating integrals. The instructor works through several examples, such as finding the area bounded by y = x^2 and y = x^3, using Riemann sums and power rules for integration. The script also addresses more complex scenarios, like areas involving trigonometric functions and linear equations, and emphasizes the importance of correctly identifying the limits of integration and the functions to be integrated.
Takeaways
- 📚 The video covers solving calculus problems to find areas of regions bounded by curves using both vertical and horizontal cross-sections.
- 📐 The first problem involves finding the area between y = x^2 and y = x^3 using two different methods, emphasizing that the area remains constant regardless of the method used.
- 📉 The script explains the process of setting up integrals for vertical cross-sections with rectangles of width DX and for horizontal cross-sections with rectangles of width DY.
- 🔍 The importance of identifying the top and bottom functions for each interval is highlighted, as this determines the order of subtraction in the integral.
- ✍️ The video demonstrates the use of antiderivatives and the power rule for integration to find the areas of the regions.
- 📈 The script includes examples of evaluating integrals by hand and using a calculator for more complex problems, such as those involving trigonometric functions.
- 📝 The process of finding points of intersection for the functions is shown to be crucial for setting the limits of integration.
- 🤔 The video points out the complexity of certain problems, such as when the right and left functions change, necessitating separate integrals.
- 📉 The script discusses the challenges of using horizontal cross-sections for certain problems and the preference for vertical cross-sections in those cases.
- 📝 The video provides a step-by-step walkthrough of solving a problem involving the natural logarithm function to find the value of K for a given area.
- 📊 The final examples include finding areas enclosed by trigonometric functions and linear functions, emphasizing the use of calculators for efficiency.
Q & A
What is the main topic of the video?
-The video is about solving calculus problems to find the area of regions bounded by different functions using both vertical and horizontal cross-sections.
How many different ways are discussed in the video to find the area of a region?
-Two different methods are discussed: using vertical cross-sections and horizontal cross-sections.
What is the first problem discussed in the video?
-The first problem is to find the area of the region bounded by y = x^2 and y = x^3.
What is the significance of the points of intersection in the problems discussed?
-The points of intersection are the limits of integration for the area calculations, marking the boundaries of the region for which the area is being calculated.
How does the video demonstrate that the area of the region remains the same regardless of the method used?
-The video shows that when the area is calculated using both vertical and horizontal cross-sections, the final result is the same, demonstrating the consistency of the area calculation.
What is the antiderivative used for the function y = x^2 in the video?
-The antiderivative of y = x^2 is (x^3)/3.
What is the integral calculated for the region bounded by y = √x and y = 1/4x in the video?
-The integral calculated for the region bounded by y = √x and y = 1/4x is 32/3.
What is the issue with using a horizontal cross-section for the problem involving y = 2 - x^2 and y = x?
-The issue with using a horizontal cross-section for this problem is that the right and left functions change at the point of intersection, making it more complex and requiring the problem to be split into two integrals.
How does the video handle the problem with the function y = 1/X from x = 2 to x = K where the area is equal to ln(4)?
-The video sets up an integral for the area from x = 2 to x = K and uses properties of logarithms to solve for K, finding that K equals 8.
What is the final area calculated for the region enclosed by y = 3cos(x) and y = x in the first quadrant?
-The final area calculated for the region enclosed by y = 3cos(x) and y = x in the first quadrant is 2.078.
Outlines
📚 Calculating Area Between Curves Using Vertical and Horizontal Cross Sections
This paragraph introduces a video lesson on solving calculus problems to find areas between curves. The focus is on unit 7 homework problems 21 through 34, specifically using vertical and horizontal cross sections to find the area bounded by y=x^2 and y=x^3. The instructor explains the process of setting up integrals with respect to x (dx) and y (dy), and emphasizes that the area should be consistent regardless of the method used. The first example involves finding the area between the curves from x=0 to x=1 using a vertical cross section, calculating the area as 1/12. The process includes identifying the intersection points, setting up the integral, and evaluating it to find the area.
📐 Horizontal Cross Section Method for Area Calculation
The second paragraph continues the discussion on finding the area between curves but introduces the horizontal cross section method. The instructor explains the process of converting the equations to be in terms of y to solve for x, which is necessary for integrating with respect to y (dy). The example provided involves the same curves as before but now with the integration limits and functions rearranged to reflect the horizontal approach. The instructor demonstrates the integration process and evaluates it to find the area, which matches the result from the vertical cross section method.
🔍 Detailed Analysis of Area Between Curves with Multiple Intersection Points
This paragraph delves into a more complex problem where the area between the curves y=√x and y=1/4x is to be found. The instructor first identifies the intersection points and then sets up the integral for a vertical cross section. The process involves integrating from x=0 to x=16, using the difference between the two functions as the height of the rectangles in the Riemann sum. The antiderivative is calculated, and the area is evaluated to be 32/3. The paragraph also attempts a horizontal cross section approach but acknowledges the complexity due to the need to solve for x in terms of y and the presence of multiple intersection points.
📉 Integrating Horizontal Cross Sections with U-Substitution
The fourth paragraph discusses the horizontal cross section method for a different set of curves, y=2-x^2 and y=x. The instructor identifies the intersection points and sets up two integrals due to the change in the right function at the point of intersection. The integrals are set up from y=-2 to y=1 and from y=1 to y=2, with the respective functions for the right and left sides of the rectangle. The instructor uses a calculator to find the area, which turns out to be 9/2, after a brief discussion on the complexity of integrating the square root function.
📈 Area Calculation with Changing Functions in Horizontal Cross Sections
The fifth paragraph presents a scenario where the horizontal cross section method is not straightforward due to the functions touching the same curve at different points. The instructor discusses the need to split the integral into two parts and to solve the equations for x in terms of y. The example involves the curves y=√x and y=x-2, with the integrals set up from y=-2 to y=0 and from y=0 to y=2. The area calculation is shown to be 16/3, demonstrating the process of integrating with respect to y and evaluating the results.
🤔 Avoiding Vertical Cross Sections for Certain Problems
In this paragraph, the instructor advises against using vertical cross sections for certain problems due to the complexity of having the same function on top and bottom, which would require solving for y. The example given involves the curves x=1/2y^2 and y=-1/2x+3, and the instructor recommends using horizontal cross sections instead. The intersection points are identified, and the functions are rewritten in terms of x for the horizontal cross section. The integral is set up from y=-6 to y=2, and the area is calculated to be 44 2/3.
📌 Finding Intersection Points for Horizontal Cross Sections
The instructor discusses how to find intersection points for horizontal cross sections, using the curves y=-1/2x+3 and x=1/2y^2 as an example. The functions are labeled, and the intersection points are calculated to be (2,2) and (18,-6). The integral is set up from y=-6 to y=2, and the right and left functions are identified for the horizontal cross section. The area is calculated using the difference between the functions, resulting in an area of 32/3.
🔍 Solving for Intersection Points and Calculating Areas
This paragraph involves identifying intersection points and calculating areas for the curves y=x^2 and y=-4x. The instructor finds the intersection points to be (-4,16) and (0,0) and sets up the integral for a vertical cross section from x=-4 to x=0. The integral involves the difference between the two functions, and the area is calculated to be 32/3. The horizontal cross section method is also discussed, with the integral set up from y=0 to y=16, and the area is found to be the same as with the vertical method.
📘 Complex Area Calculations with Multiple Intersections and Functions
The instructor tackles a complex problem involving the curves x=1/2y^2 and y=-1/2x+3, which require careful identification of intersection points and the correct setup of integrals for horizontal cross sections. The intersection points are found to be (2,2) and (18,-6). The integral is split into two parts due to the change in the function at the intersection point. The area calculation involves integrating the difference between the functions from y=-6 to y=2, resulting in an area of 42 2/3.
📌 Finding the Value of K for a Given Area Under 1/X
The final paragraph involves finding the value of K for which the area under the curve y=1/X from x=2 to x=K is equal to the natural logarithm of 4. The instructor sets up the integral for a vertical cross section from x=2 to x=K and evaluates it to find the area. Using properties of logarithms, the equation is simplified to find that the absolute value of K is 8, leading to the conclusion that K is 8, assuming K is greater than 2.
📐 Equal Areas Under Cosine Function and X-Axis
This paragraph discusses finding the value of C that divides the area under the curve y=cosine(X) between x=0 and x=π/2 into two equal parts. The instructor sets up two integrals, one from x=0 to x=C and another from x=C to x=π/2, and equates them to find C. By solving the resulting trigonometric equation, the value of C is found to be π/6, which corresponds to an angle of 30 degrees in Quadrant 1.
📊 Area Enclosed by y=3cosine(X) and y=X in the First Quadrant
The instructor calculates the area enclosed by the y-axis, the curve y=3cosine(X), and the line y=X in the first quadrant. Using a calculator, the intersection point is found to be at (1.7, 3cosine(1.7)). The integral is set up as a DX problem from x=0 to x=1.7, integrating the difference between the two functions. The resulting area is calculated to be approximately 2.078, demonstrating the process of using a calculator to solve integrals for area calculations.
Mindmap
Keywords
💡Area
💡Integration
💡Riemann Sum
💡Vertical Cross-Section
💡Horizontal Cross-Section
💡Antiderivative
💡Power Rule
💡Intersection Points
💡Graphs
💡Natural Logarithm
💡Cosine Function
Highlights
Introduction to solving unit 7 homework problems 21 through 34 using calculus.
Explaining how to find the area of a region bounded by two functions using vertical and horizontal cross-sections.
Demonstration of setting up a Riemann sum for a vertical cross-section integral.
Integration from x=0 to x=1 using the difference of two functions to find the area under a curve.
Using the antiderivative to evaluate the integral and find the area of the region.
Switching to a horizontal cross-section to solve the same problem and comparing results.
Solving for the area using horizontal cross-sections and the dy method.
Finding the area of a region bounded by y=√x and y=1/4x using vertical cross-sections.
Verification of intersection points for the functions y=√x and y=1/4x.
Calculating the area using the difference of the functions and the power rule for integration.
Approach to solving the area problem using horizontal cross-sections and dy integration.
Finding the area of the region bounded by y=2-x^2 and y=x using vertical cross-sections.
Explanation of why horizontal cross-sections are not suitable for certain problems due to function intersections.
Solving the area problem for y=x^2 and y=-4x using both vertical and horizontal cross-sections.
Use of properties of logarithms to find the value of K for a given area under 1/x from x=2 to x=K.
Finding the area enclosed by y=cos(x) and the x-axis from 0 to π/2 and determining the value of C.
Final problem involves finding the area in the first quadrant enclosed by y=3cos(x) and y=x.
Using a calculator to find the area of the region bounded by two functions and the axes.
Transcripts
Browse More Related Video

Calculus AB Homework 7.4 Disk and Washer Method

Calculus AB Lesson 7.3: Area Between Curves

Area Between y=x^3 and y=3x-2 | MIT 18.01SC Single Variable Calculus, Fall 2010

Finding The Area Under The Curve Using Definite Integrals - Calculus
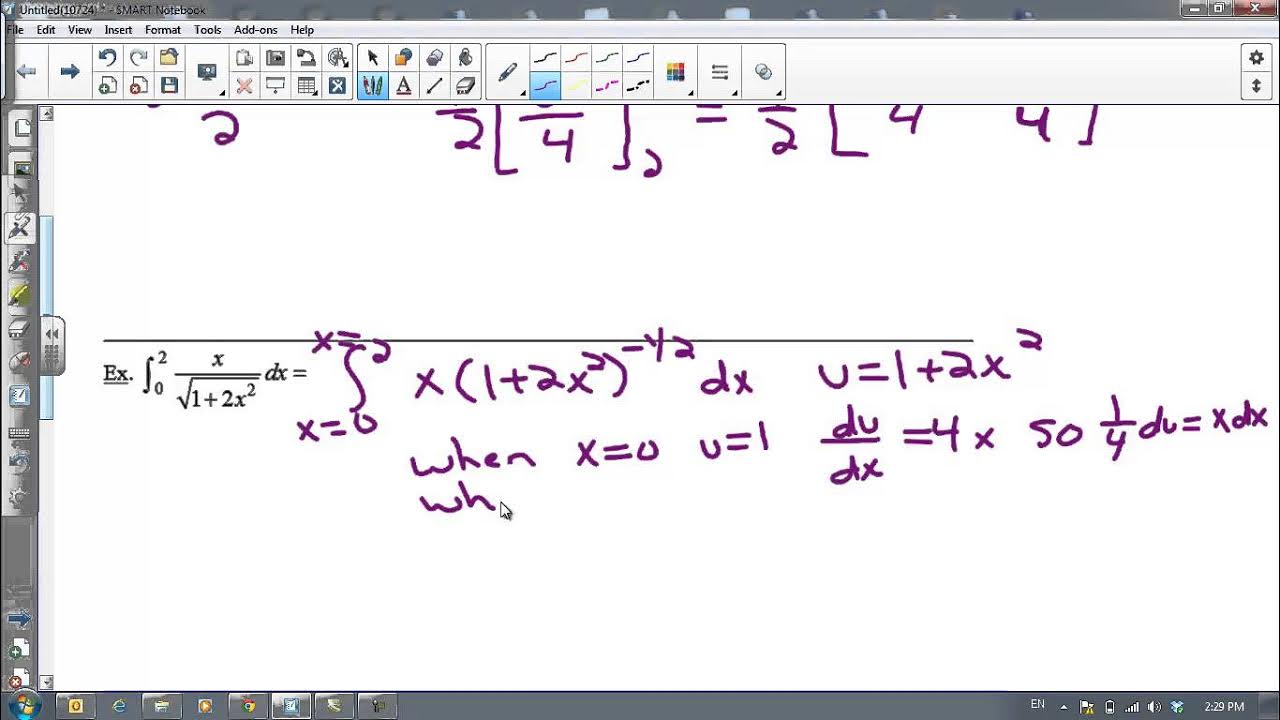
U-Substitution with Definite Integrals
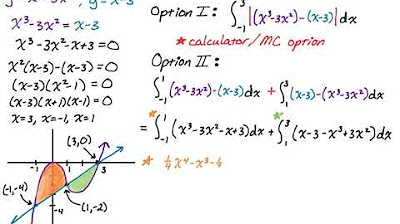
Area Between Two Curves with Multiple Regions: y = x^3-3x^2 and y = x-3
5.0 / 5 (0 votes)
Thanks for rating: