Calculus 1 Lecture 5.1: Finding Area Between Two Curves
TLDRThe transcript is an educational dialogue focused on the application of integrals to find the area between two curves, a concept in calculus. The speaker introduces the topic by explaining that the area between two curves can be found by subtracting the integral of the lower curve from the integral of the upper curve, emphasizing that the result will always be positive if calculated correctly. The discussion then delves into the specifics of setting up integrals to find these areas, highlighting the importance of identifying the correct order of functions (upper and lower) and the intervals over which they are integrated. The speaker also addresses the scenario where the curves intersect at multiple points, necessitating separate integrals for each interval. Practical applications, such as determining the distance between two racing cars based on their velocity curves, are also explored to illustrate the real-world relevance of the concept. The transcript concludes with a problem-solving approach that involves finding the intersection points of the curves, determining which function is on top over specific intervals, and setting up the integrals accordingly. The speaker provides a detailed walkthrough of the process, including the setup for the integrals and the evaluation of the areas, offering students a comprehensive understanding of the material.
Takeaways
- 📐 The concept of finding the area between two curves is introduced, emphasizing that it's an application of integrals that students have been using all along.
- 🔍 To find the area between two curves, you subtract the integral of the lower function from the integral of the upper function over the given interval.
- ⚖️ The resulting area between the curves is always positive, indicating that if a negative area is found, an error has been made in the setup.
- 📈 The technique involves setting up an integral from point A to B, where one function (F(x)) is above the other (G(x)) for the entire interval.
- 🔑 It's crucial to identify the correct order of the functions (F(x) > G(x)) to ensure the area calculated is the desired one.
- 🤔 The method can be visualized by considering the area under the upper function and then subtracting the area under the lower function.
- 📉 When dealing with curves that intersect, it's necessary to find the points of intersection to determine the correct intervals for integration.
- 🧩 The process can be simplified by combining the integrals if they share the same bounds, leveraging the properties of integral calculus.
- 🏎️ An application of the concept is illustrated through a racing car scenario, where the area between velocity curves over time represents the distance between two cars at the end of the race.
- 📋 The importance of considering the correct bounds and the order of functions is highlighted, especially when the functions do not simplify to a single expression in terms of the variable of integration.
- 🔄 The strategy of switching variables (from X to Y or vice versa) to simplify the problem is discussed, showing an alternative approach when dealing with functions that are not easily integrable in the original variable.
Q & A
How is the area between two curves found?
-The area between two curves is found by subtracting the integral of the lower curve from the integral of the upper curve over the given interval. This is represented mathematically as ∫(from A to B) [f(x) - g(x)] dx, where f(x) is the upper function and g(x) is the lower function for the interval [A, B].
Why is the area between two curves always positive?
-The area between two curves is always positive because the integral represents a signed area. When subtracting the integral of the lower curve from the upper curve, the result is the net positive area between them. If a negative area were calculated, it would indicate an error in the setup of the integral, such as reversing the order of the functions.
What is the condition for the function f(x) relative to g(x) for the area between the curves to be correctly calculated?
-For the area between the curves to be correctly calculated, f(x) must be greater than or equal to g(x) for all x in the interval [A, B]. This ensures that f(x) is always above g(x), making the subtraction of their integrals yield a positive area.
How do you determine which function is on top between two given functions?
-To determine which function is on top, you can plug in a test value within the interval of interest into both functions and compare the results. The function that yields the higher value at the test point is the one on top.
What is the significance of finding the intersection points of two curves when calculating the area between them?
-The intersection points of two curves are the boundaries of the interval over which the integral is evaluated to find the area between the curves. These points are critical to identify the limits of integration and to ensure that the correct area is calculated.
How can the concept of area between two curves be applied to real-life scenarios, such as racing cars?
-In real-life scenarios like racing cars, the area between two velocity curves over time can represent the distance between two vehicles at the end of the race. By integrating the difference in velocities over the race duration, you can find the distance by which one car is ahead of the other.
What is the correct setup for an integral when finding the area between two curves that intersect at more than two points?
-When two curves intersect at more than two points, you will have multiple intervals over which the area is calculated. This results in setting up multiple integrals, one for each interval between the intersection points. Each integral represents the area under one function minus the area under the other for that specific interval.
Why is it important to consider the order of functions when setting up an integral for the area between two curves?
-The order of functions is important because it determines which function is considered to be above the other, which in turn affects the sign of the area calculated. If the order is reversed, the sign of the calculated area will be incorrect, leading to an inaccurate representation of the distance or area between the curves.
How can you find the area between two curves when the functions are given in terms of y instead of x?
-If the functions are given in terms of y, you can still find the area between the curves by integrating with respect to y. You would set up the integral as ∫(from C to D) [h(y) - g(y)] dy, where h(y) and g(y) are the two functions expressed in terms of y, and the integration is performed over the interval [C, D] on the y-axis.
What is the advantage of changing the variable of integration from x to y or vice versa?
-Changing the variable of integration can simplify the problem, especially when the functions are more naturally expressed in terms of one variable over the other. It can make it easier to identify the correct setup for the integral and to perform the integration, leading to a more straightforward solution.
How do you handle a situation where the functions defining the curves are not directly integrable with respect to the chosen variable?
-If the functions are not directly integrable with respect to the chosen variable (x or y), you may need to manipulate the functions, such as by taking square roots, completing the square, or using other algebraic techniques to express them in a form that is integrable. Alternatively, you can switch the variable of integration to the one that allows for easier integration.
Outlines
📐 Understanding Area Between Two Curves
The paragraph introduces the concept of finding the area between two curves, which are real-life functions. It explains that this involves calculating the difference between the areas under two curves, where one curve is always above the other within a given interval. The process is simplified by subtracting the area under the lower curve from the area under the upper curve. The importance of ensuring the result is a positive area is emphasized, as it represents the actual space between the curves.
🔍 Combining Integrals for Area Calculation
This section discusses the mathematical convenience of combining two integrals that share the same bounds of integration to find the area between two curves. It highlights that the order of operations can be reversed, allowing for the integration of both areas and then finding their difference. The importance of the upper function being greater than the lower function to ensure a positive result is reiterated. The paragraph also clarifies that the method is applicable when the bounds for both functions are identical.
🤔 Visualizing and Solving the Area Problem
The paragraph delves into the practical application of finding the area between two curves by first visualizing the curves and their relationship to the x-axis. It explains that the process involves finding the area under the curve, subtracting the area below the x-axis, and understanding that the function above the x-axis will always yield a positive area. The connection between the absolute value method and the area between two curves is also established, showing that they can be used interchangeably for calculating total areas.
📈 Setting Up and Solving Word Problems
This segment focuses on setting up and solving word problems related to finding areas between curves. It emphasizes the importance of identifying the correct interval and determining which function is on top or bottom within that interval. The paragraph provides a step-by-step approach to solving these problems, including the need to use parentheses for clarity and the significance of including all terms in the integral for accurate results.
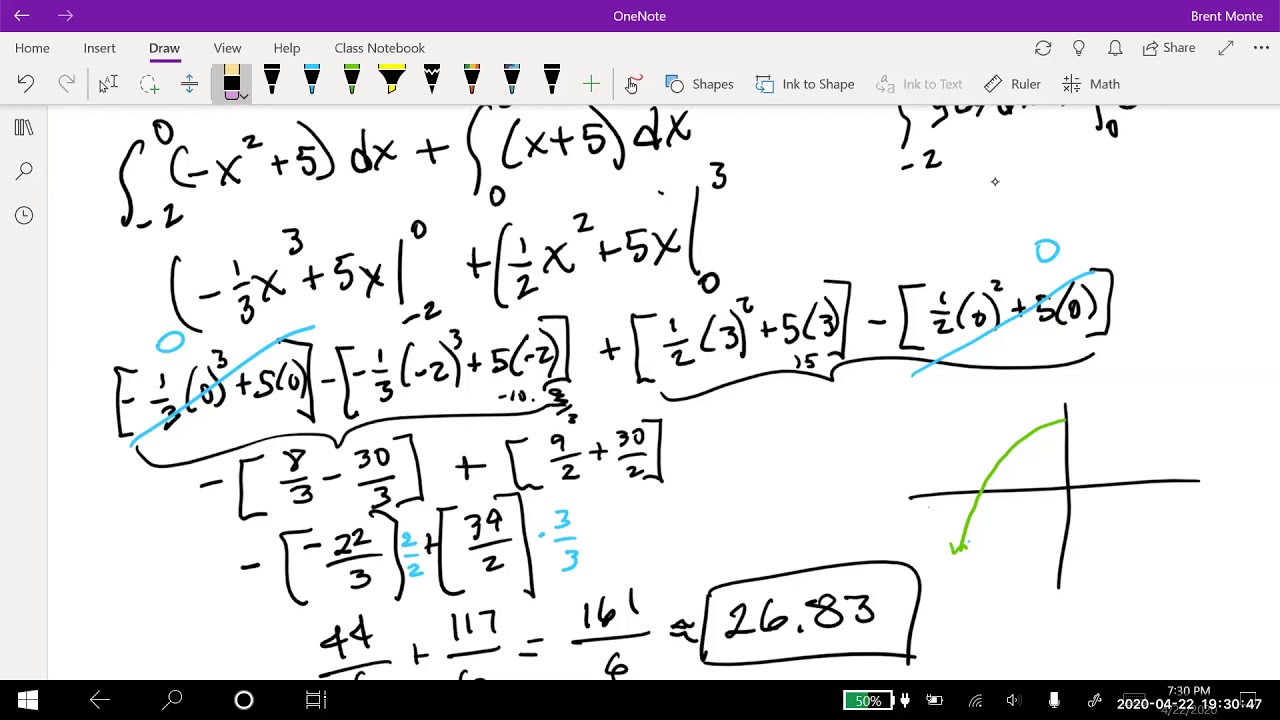
🧮 Evaluating Definite Integrals for Area
The paragraph demonstrates how to evaluate definite integrals to find the area between two curves. It shows the process of simplifying the integral expression and then evaluating it between the given bounds. The importance of plugging in the correct values and being mindful of the signs is highlighted. The paragraph also touches on the concept of finding the area bound by a curve and the x-axis, which is a simplified version of the area between two curves.
🏎️ Applying the Concept to Racing Cars
This section presents a real-world application of the concept, using the example of a car race. It explains how the area between two velocity curves over time can represent the distance between two cars at the end of the race. The paragraph illustrates how integrating velocity with respect to time can yield the distance traveled, providing a quantitative measure of the lead in a race.
🤹♂️ Dealing with Functions in Terms of Y
The paragraph addresses a more complex scenario where functions are given in terms of Y rather than X. It discusses the need to solve for X in terms of Y to find the bounds of integration and to set up the integral correctly. The process involves finding the points of intersection and determining the correct order of functions (which is on top and which is on the bottom) within the given interval. The paragraph also highlights the importance of considering all relevant points, including the starting point of the curve on the x-axis.
🧠 Switching Variables for Easier Integration
The final paragraph suggests an alternative approach when dealing with functions in terms of Y by switching the roles of X and Y to simplify the integration process. It demonstrates that by treating the problem in terms of Y, the calculation can be made easier, especially when there's a clear top function throughout the interval of integration. The paragraph emphasizes the need to be cautious with the bounds of integration when switching variables and to ensure that the setup for the integral accurately reflects the problem's requirements.
Mindmap
Keywords
💡Integrals
💡Area between curves
💡Bounds of integration
💡Velocity curves
💡Definite integral
💡Graphing
💡Quadratic formula
💡Distance
💡Racing cars
💡Parabolas
💡Substitution
Highlights
The concept of finding the area between two curves by subtracting the integral of the lower function from the integral of the upper function.
The importance of ensuring the area calculated is always positive, indicating a correct setup of the integral.
The method of determining which function is on top by testing a point within the interval of interest.
The strategy of setting up integrals to find the area between curves, emphasizing the need to identify the correct interval and which function is above the other.
The application of integrals to real-life scenarios, such as calculating the distance between two racing cars based on their velocity curves.
The use of the absolute value in integrals to account for areas below the x-axis when finding the total area under a curve.
The process of finding the x-coordinates of curve intersections to determine the interval over which to integrate.
The approach to solving integrals when the order of functions changes within the interval, resulting in separate integrals for each segment.
The emphasis on the importance of parentheses in integrals to ensure the correct application of signs and order of operations.
The illustration of how to handle integrals when the curves intersect at more than two points, potentially requiring multiple integrals to cover all areas.
The concept that the area under a velocity curve over a time interval represents the distance traveled, providing a practical application of integrals.
The method of evaluating definite integrals by plugging in the bounds of integration and simplifying the expression.
The explanation of how to find the area bounded by a curve and the x-axis by setting the curve equal to zero and integrating.
The demonstration of solving a more complex problem involving functions that are not explicitly in terms of x, by transforming the given functions into x terms.
The strategy of changing variables to y and integrating with respect to y when the functions are more easily expressed in terms of y, simplifying the integral setup.
The reminder to be cautious with the bounds of integration when switching variables, ensuring that the limits are correctly applied to the new variable.
The final demonstration of evaluating the integral in terms of y, showing that the result is consistent with the method done in terms of x, but with a simpler process.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: