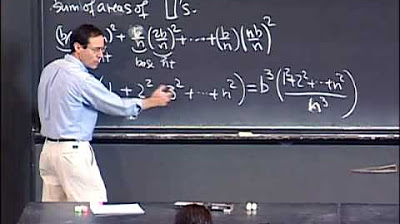Business Calculus - Math 1329 - Section 5.3 - The Definite Integral and Fundamental Thm of Calculus

Doug Ray

17 Apr 202040:49

EducationalLearning

32 Likes 10 Comments

TLDRThis video script offers an in-depth exploration of the definite integral and the fundamental theorem of calculus. It begins with a group activity involving a GeoGebra app, where participants manipulate rectangles to approximate the area under a curve defined by the function f(x) = 5 - 1/4x^2. The concept of Riemann sums is introduced as a method to estimate areas, with a shift from left to right rectangles indicating a change in approximation. The script then delves into calculating areas under curves using regular partitions and left rectangles, leading to the definition of a Riemann sum and its significance in finding definite integrals. The fundamental theorem of calculus is presented, linking antiderivatives to the evaluation of definite integrals over an interval. The video concludes with examples of evaluating definite integrals, properties of integrals, and a teaser for future lessons on applications of the definite integral, such as the Gini index and calculating areas of shapes.

Takeaways

📐 The definite integral represents the signed area under a curve from one point to another and is a fundamental concept in calculus.
📈 The concept of Riemann sums is used to approximate the area under a curve by breaking it down into rectangles, which is critical for understanding definite integrals.
➗ The process of finding the area under a curve involves using a function, partitioning the interval, and calculating the sum of the areas of the rectangles (Riemann sums).
🔍 The choice between left, right, or midpoint rectangles in a Riemann sum can affect the accuracy of the approximation and whether the result is an over- or underestimate.
📊 As the number of rectangles (n) increases, the approximation of the area under the curve becomes more accurate, converging to the actual area.
∫ The definite integral is denoted by ∫ and is the limit of the Riemann sums as the number of rectangles approaches infinity.
🔄 The Fundamental Theorem of Calculus connects derivatives and integrals, stating that the definite integral from A to B of a function can be found by evaluating the antiderivative at the endpoints and subtracting.
🔢 The properties of definite integrals allow for manipulations such as negation when reversing limits, scaling by a constant, and splitting the integral into parts.
🔁 The ability to split the integral at any point (C) and sum the parts to find the total area under the curve from A to B is a powerful property for solving complex integrals.
⛓ The definite integral can be evaluated using substitution, particularly useful for integrals involving complex expressions or roots.
📋 The process of evaluating a definite integral involves finding an antiderivative, applying the limits of integration, and simplifying the expression to find the area.
🔢 The definite integral has practical applications in various fields, including calculating areas of irregular shapes and understanding the Gini index in economics.

Q & A

What is the main topic of section 5.3?
-The main topic of section 5.3 is the definite integral and the fundamental theorem of calculus, which involves concepts such as area under the curve, Riemann sums, and applications of definite integrals.
What does the variable 'n' represent in the context of the geogebra file exercise?
-In the context of the geogebra file exercise, 'n' represents the number of rectangles that are drawn to approximate the area under the curve.
What is the difference between a right rectangle and a left rectangle in the geogebra app?
-A right rectangle starts from the right endpoint of the subinterval and reaches the height of the function at that point, while a left rectangle starts from the left endpoint of the subinterval.
What is the purpose of using the sliders in the geogebra exercise?
-The purpose of using the sliders is to change the values and fill out the information in the table to notice patterns and analyze the data regarding the approximation of the area under the curve.
How does the concept of a Riemann sum relate to the definite integral?
-A Riemann sum is a way to approximate the definite integral by summing the areas of rectangles under the curve. As the number of rectangles (n) increases, the Riemann sum becomes a better approximation of the actual area under the curve, which is the definite integral.
What is the fundamental theorem of calculus, and how does it relate to the definite integral?
-The fundamental theorem of calculus states that the definite integral from A to B of a function f(x) is equal to the antiderivative F(x) evaluated from B to A (F(B) - F(A)). It provides a method to evaluate definite integrals by finding an antiderivative of the integrand and applying the limits of integration.
Why is it always an underestimate when using left rectangles to approximate the area under the curve?
-It is always an underestimate because the rectangles are always below the curve, and there is always some space under the curve that is not considered by the rectangles.
What is the significance of the 'signed area' in the context of definite integrals?
-Signed area refers to the concept that areas below the x-axis are considered negative, while areas above the x-axis are positive. This is important for understanding the definite integral's value when the function crosses the x-axis within the interval of integration.
How can you create an overestimate of the area under the curve using rectangles?
-You can create an overestimate by using right rectangles or by using a midpoint method, where the height of the rectangle is determined by a point that is higher on the curve, thus covering more area above the curve.
What is the relationship between the definite integral and the antiderivative?
-The definite integral of a function over an interval can be found by evaluating the antiderivative of the function at the upper and lower limits of the interval and subtracting the two.
What are some properties of definite integrals that can help simplify calculations?
-Some properties include: (1) The integral from a to a is zero, (2) The integral from A to B is equal to the negative of the integral from B to A, (3) The integral of a constant times a function is equal to the constant times the integral of the function, (4) The integral of the sum of functions is equal to the sum of the integrals of the functions, and (5) The integral over an interval can be split into the sum of integrals over subintervals.
How can you evaluate a definite integral using substitution?
-You can evaluate a definite integral using substitution by choosing a substitution (u) that simplifies the integrand, then finding du (the differential of u), and substituting back into the integral after integrating with respect to u. Finally, apply the limits of integration to find the value of the integral.

Outlines

00:00

📚 Introduction to Definite Integrals and Riemann Sums

This paragraph introduces the concept of definite integrals and the fundamental theorem of calculus. It discusses the area under a curve, Riemann sums, and the use of GeoGebra to visualize and approximate areas using rectangles. The focus is on understanding the difference between left and right rectangles and how they are used to estimate the area under a curve. The paragraph also includes an exercise to be completed using a provided GeoGebra file and concludes with a transition to a manual example to solidify understanding.

05:06

📏 Estimating Areas with Rectangles and Delta X

The second paragraph delves into the process of estimating the area under a curve using rectangles. It explains the concept of a regular partition and how to calculate the width of each subinterval (Delta X). The paragraph outlines the steps to fill out a table for an example function, emphasizing the use of left rectangles to determine the height of each rectangle. It also discusses how to calculate the area of each rectangle and sum them to approximate the total area under the curve, noting that this method typically results in an underestimate.

10:08

📈 Understanding Riemann Sums and Their Application

This section explains the formal definition of a Riemann sum, named after the mathematician Riemann. It describes how to partition an interval into subintervals and choose a point within each subinterval to determine the height of the rectangles used in the sum. The paragraph also discusses the concept of signed area and how Riemann sums can be used to find the definite integral, which is the limit of the Riemann sums as the number of rectangles approaches infinity.

15:09

🧮 The Definite Integral and Its Calculation

The fourth paragraph introduces the notation for the definite integral and explains its relationship with Riemann sums. It discusses how the definite integral can be calculated as the limit of Riemann sums and how it represents the exact area under a curve. The paragraph also touches on the concept of signed area and the importance of using limits in calculus. It concludes with a GeoGebra exercise to help visualize the concept of definite integrals.

20:13

🔢 Evaluating Definite Integrals Using Antiderivatives

The paragraph explains the process of evaluating definite integrals using antiderivatives, as stated by the fundamental theorem of calculus. It provides an example of how to find the antiderivative of a function and then evaluate the definite integral over a given interval by substituting the limits of integration into the antiderivative and subtracting. The paragraph emphasizes the importance of maintaining the correct order of evaluation (upper limit minus lower limit) to avoid obtaining a negative result.

25:16

🔴 Properties and Applications of Definite Integrals

This section covers several properties of definite integrals, such as the integral over a single point being zero, the integral's reversal property, the ability to scale integrals by a constant, and the distributive property over addition and subtraction. It also discusses the additivity of integrals, which allows for the splitting of integration intervals. The paragraph provides examples of how to apply these properties to solve various integral problems, including using given integral values to find new integrals and using substitution for more complex integrals.

30:17

📝 Definite Integration with Substitution and Upcoming Topics

The final paragraph demonstrates how to perform definite integration with substitution, using an example integral involving the square root of a function. It shows the steps to perform the substitution, evaluate the indefinite integral, and then apply the limits of integration to find the definite integral. The paragraph concludes with a teaser for the next lesson, which will cover more applications of the definite integral, including the Gini index and finding areas of shapes using definite integrals.

Mindmap

Keywords

💡Definite Integral

The definite integral is a fundamental concept in calculus that represents the signed area under a curve between two points on the x-axis. It is used to calculate the accumulated value of a function over an interval. In the video, it is central to understanding how to approximate areas using rectangles and the concept of Riemann sums, which are integral to the fundamental theorem of calculus.

💡Riemann Sum

A Riemann sum is a method for approximating the definite integral of a function. It involves breaking the area under the curve into rectangles and summing their areas. The video explains that as the number of rectangles increases, the approximation becomes more accurate, illustrating the concept with a function f(x) = x^2 + 1 over the interval from 3 to 7.

💡Fundamental Theorem of Calculus

The fundamental theorem of calculus is a critical link between differentiation and integration. It states that the definite integral of a function can be found by evaluating the antiderivative of the function at the upper and lower limits of the interval and subtracting the results. This theorem is showcased in the video by demonstrating how to evaluate definite integrals using antiderivatives.

💡Antiderivative

An antiderivative is a function whose derivative is the original function in question. In the context of the video, finding an antiderivative is a crucial step in evaluating definite integrals using the fundamental theorem of calculus. The process involves reversing the operation of differentiation to find the original function.

💡GeoGebra

GeoGebra is a dynamic mathematics software that allows for visualization of mathematical concepts. In the video, GeoGebra is used to illustrate the process of approximating the area under a curve by drawing rectangles, which helps in understanding the concept of Riemann sums and the definite integral.

💡Signed Area

Signed area refers to the concept of assigning a positive or negative value to the area under a curve depending on whether it lies above or below the x-axis. This concept is important in integral calculus and is discussed in the video when explaining that integrals can represent areas that are below the x-axis as negative.

💡Partition

In the context of the video, a partition refers to dividing the interval under consideration into equal subintervals. This is a step in the process of calculating Riemann sums and is essential for approximating the definite integral by creating a series of rectangles under the curve.

💡Rectangles Under the Curve

The method of drawing rectangles under the curve is a visual technique used to approximate the area under the curve, which is the basis for the concept of the definite integral. The video explains how to use left and right rectangles to estimate this area and how the process leads to the definition of a Riemann sum.

💡Limit

In calculus, a limit is a value that a function or sequence approaches as the input (or index) approaches some value. The concept of a limit is central to the definition of the definite integral, as it is the value that the Riemann sum approaches as the number of rectangles (and thus the partitions) goes to infinity.

💡Integration by Substitution

Integration by substitution is a technique used to evaluate integrals that involve complicated expressions. In the video, it is demonstrated by letting u be a suitable expression in terms of x and then changing the variable of integration to u, which simplifies the integral and makes it easier to solve.

💡Properties of Definite Integrals

The video outlines several properties of definite integrals, such as the integral over a single point being zero, the integral from A to B being the negative of the integral from B to A, and the linearity of integrals, which allows for the splitting of integrals and multiplication by constants. These properties are essential for manipulating and solving integrals in calculus.

Highlights

Section 5.3 introduces the concept of the definite integral and the Fundamental Theorem of Calculus, focusing on area under curves, Riemann sums, and their applications.

A group activity using a GeoGebra file on a website is designed to visualize the function f(x) = 5 - 1/4x^2 and explore the concept of left and right rectangles.

The difference between left and right rectangles is explained in the context of partitioning an interval and determining the height of the rectangles.

The objective of the activity is to approximate the actual area under the curve using the concept of Riemann sums and adjusting the number of rectangles.

Patterns and breaks in the pattern are to be analyzed when switching from left to right rectangles to understand the approximation of the area.

A manual example demonstrates estimating the area under the curve of f(x) = x^2 + 1 over the interval from 3 to 7 using 8 left rectangles.

The process of calculating the width of subintervals (Δx) and the height (f(x_i*)) for each rectangle is detailed in the example.

The concept of a Riemann sum is introduced, which is a way to estimate the area under a curve using rectangles, named after the mathematician Riemann.

The definite integral is defined as the limit of Riemann sums as the number of rectangles (n) approaches infinity, providing an exact value for the area under the curve.

The Fundamental Theorem of Calculus is presented, linking antiderivatives to definite integrals and providing a method to evaluate definite integrals.

Examples are provided to illustrate the process of evaluating definite integrals using antiderivatives and the rules of limits.

The concept of 'signed area' is explained in the context of definite integrals, which accounts for the function's position relative to the x-axis.

Properties of definite integrals are discussed, including the behavior of integrals with respect to constant factors, sums, and interval manipulation.

A method for definite integration using substitution is demonstrated with an example, showcasing a technique to handle more complex integrands.

The application of definite integral properties is shown through a series of problems, highlighting the ability to split and recombine integrals.

The importance of Riemann sums in understanding the foundation of calculus is emphasized, despite the preference for using definite integrals for precision.

The session concludes with a preview of upcoming topics, such as the Gini index and finding areas of shapes using definite integrals.

Transcripts

Browse More Related Video

Math 1325 Lecture 13 2

Definite Integrals!

Lec 18 | MIT 18.01 Single Variable Calculus, Fall 2007

4.3 - Area and Definite Integrals

Fundamental theorem of calculus (Part 2) | AP Calculus AB | Khan Academy

Riemann Sums and Definite Integrals

Related Tags

Definite Integrals Riemann Sums Calculus Geogebra Area Under Curve Fundamental Theorem Left Rectangles Right Rectangles Mathematical Analysis Educational Content Integral Calculus