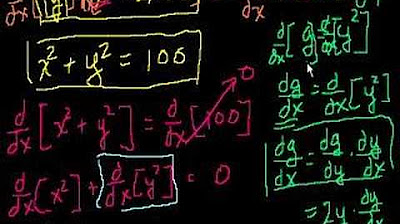Implicit Differentiation
TLDRThis video script delves into the concept of implicit differentiation, a method used to find the derivative of a function when it's not explicitly given. The script begins by explaining the process of implicit differentiation using the example of the equation x^2 + y^2 = 100, and how to find dy/dx at a specific point. It then progresses to more complex examples involving the product rule and trigonometric functions, demonstrating how to isolate dy/dx and solve for it. The script culminates in finding the second derivative and evaluating it at a given point, reinforcing the importance of understanding implicit differentiation for solving mathematical problems.
Takeaways
- 📚 Implicit differentiation is used to find the derivative of a function when it is not explicitly given in the form y = f(x).
- 🔢 The process involves differentiating both sides of an equation with respect to x, taking care to treat y as a function of x by including the term dy/dx.
- 📈 When differentiating a power function with respect to x, the power rule is applied, and terms like y^3 with respect to x become 3y^2 * (dy/dx).
- 🌐 The video provides an example where the equation x^2 + y^2 = 100 is differentiated to find dy/dx, resulting in dy/dx = -x/y.
- 📍 To find the slope at a specific point, substitute the x and y values from the point into the derived expression for dy/dx. For example, at (6, 8), the slope is -3/4.
- 🔄 The video also demonstrates how to use the product rule and chain rule when differentiating terms involving multiplication and trigonometric functions.
- 📊 The example of x^3 + 4xy + y^2 = 13 illustrates the use of the product rule for the term 4xy and results in dy/dx = (-3x^2 - 4y) / (4x + 2y).
- 🔢 For the equation 5 - x^2 = sin(xy^2), the chain rule is applied to differentiate the trigonometric function, resulting in dy/dx = (-2x) / (cos(xy^2)).
- 📈 The video concludes with an example of finding the second derivative, d^2y/dx^2, for the equation x^3 + y^3 = 9, and evaluating it at the point (1, 2), yielding -9/16.
- 🔍 The process of implicit differentiation is shown to be a powerful tool for finding derivatives in complex equations and for evaluating slopes or rates of change at specific points.
- 📚 The importance of understanding the rules of differentiation, such as the power rule, product rule, and chain rule, is emphasized for successfully applying implicit differentiation.
Q & A
What is the main focus of the video?
-The main focus of the video is on solving problems associated with implicit differentiation.
How does the process of implicit differentiation work?
-Implicit differentiation involves differentiating both sides of an equation with respect to x, and then isolating the derivative of y with respect to x (dy/dx) on one side of the equation.
What is the derivative of x^3 with respect to x?
-The derivative of x^3 with respect to x is 3x^2.
How is the derivative of y^3 with respect to x found?
-The derivative of y^3 with respect to x is 3y^2 * (dy/dx).
What is the equation used to find the slope at a specific point?
-The slope at a specific point is found by evaluating the derivative dy/dx at the given point's coordinates, replacing x and y with their respective values.
What is the equation given in the second problem of the video?
-The equation given in the second problem is x^3 + 4xy + y^2 = 13.
How is the product rule applied in the second problem?
-The product rule is applied to differentiate the term 4xy with respect to x. It involves taking the derivative of 4x (which is 4) and multiplying it by y, and then taking the derivative of y (which is 1) and multiplying it by 4x, and adding these two results.
What is the final expression for dy/dx in the second problem?
-The final expression for dy/dx in the second problem is (-3x^2 - 4y) / (4x + 2y).
How is the chain rule applied in the third problem?
-The chain rule is applied to differentiate the term sine(x y^2) with respect to x. It involves keeping the inside function (sine) the same and multiplying by the derivative of the inside function (x y^2), which requires using the product rule again.
What is the final expression for the second derivative in the last problem?
-The final expression for the second derivative in the last problem is (-2xy^3 - 2x^3) / (y^5).
What is the value of the second derivative at the point (1,2) in the last problem?
-The value of the second derivative at the point (1,2) in the last problem is -9/16.
Outlines
📚 Introduction to Implicit Differentiation
This paragraph introduces the concept of implicit differentiation, focusing on how to differentiate equations where variables are not explicitly separated. The video begins with an example equation, x^2 + y^2 = 100, and aims to find its derivative, dy/dx. The process involves differentiating both sides with respect to x and applying rules such as the power rule for x^3 and y^3, as well as the chain rule for constants. The key takeaway is to treat y as a function of x when differentiating with respect to x, which necessitates adding the term dy/dx to the differentiation of y. The example concludes with the solution for dy/dx and its evaluation at a specific point (x=6, y=8), resulting in the slope of the tangent line at that point.
🔢 Solving for dy/dx in Various Equations
This paragraph delves into solving for the derivative dy/dx in different types of equations. It starts with a new equation, x^3 + 4xy + y^2 = 13, and explains the differentiation process, including the use of the product rule for 4xy. The explanation is detailed, highlighting the steps to isolate dy/dx and the importance of moving non-dy/dx terms to the other side of the equation. The solution for dy/dx is presented in a simplified form, and the paragraph continues with an example of evaluating the derivative at a specific point (x=1, y=2). The paragraph then moves on to discuss the process of implicit differentiation with trigonometric functions, providing a comprehensive guide on how to handle such cases.
📈 Finding Second Derivatives and Evaluating at Points
This paragraph focuses on finding the second derivative of a function and evaluating it at a given point. The video starts by differentiating both sides of the equation 5 - x^2 = sin(xy^2) with respect to x, using the chain rule and product rule. The process involves finding the first derivative dy/dx and then differentiating it again to obtain the second derivative d^2y/dx^2. The quotient rule is introduced for this step, and the calculations are detailed, leading to a complex fraction. The video demonstrates how to simplify this expression and evaluate it at the point (x=1, y=2), providing a step-by-step breakdown of the mathematical process and the final result of the second derivative at that point.
Mindmap
Keywords
💡Implicit Differentiation
💡Derivative
💡Chain Rule
💡Product Rule
💡Quotient Rule
💡Slope
💡Trigonometric Functions
💡Constants
💡Algebraic Manipulation
💡Evaluation
💡Second Derivative
Highlights
Introduction to implicit differentiation and its applications.
Given equation x^2 + y^2 = 100, find dy/dx using implicit differentiation.
Differentiating y^3 with respect to x results in 3y^2 * dy/dx.
For r^4 with respect to x, the derivative is 4r^3 * dr/dx, with dx/dx canceling out.
Derivative of x^2 is 2x and y^2 with respect to x is 2y * dy/dx.
Isolating dy/dx results in dy/dx = -x/y.
Calculating the slope at the point (6, 8) gives dy/dx = -3/4.
Differentiating the equation x^3 + 4xy + y^2 = 13 to find dy/dx.
Using the product rule for the derivative of 4xy.
Resulting expression for dy/dx is -3x^2 - 4y / 4x + 2y.
Evaluating dy/dx at the point (1, 2) gives -11/8.
Implicit differentiation with trigonometric functions, given 5 - x^2 = sin(x * y^2).
Derivative of x * y^2 using the product rule and chain rule.
Final expression for dy/dx involving trigonometric functions is (-2x - y^2 * cos(x * y^2)) / (2xy * cos(x * y^2)).
Finding the second derivative, d^2y/dx^2, for the equation x^3 + y^3 = 9.
First derivative is -x^2/y^2.
Applying the quotient rule to find the second derivative.
Simplified second derivative is (-2xy^3 - 2x^3) / y^5.
Evaluating the second derivative at (1, 2) results in -9/16.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: